THE GOVERNOR GENERAL ON LAND SURVEYING
(The Empire (Sydney, New South Wales : 1850 - 1875),
Wednesday 2 September 1857, page 3)
The following lecture, on the subject of Land Surveying, was delivered in the Hall of the School of Arts, last evening [1 September 1857], by his Excellency Sir William Denison.
Before reading the lecture, some details about the lecturer Denison and the place, the Hall of the School of Arts, are provided.

William Thomas Denison, appointed Australia’s first Governor General in 1854
Denison, Sir William Thomas (1804–1871)
William Thomas Denison was born on 3 May 1804 in London, son of John Denison and his second wife Charlotte, née Estwick. Like his brothers Evelyn (Viscount Ossington) and Edward (bishop of Salisbury) he went to Eton; he later entered the Royal Military College, graduating in 1826 as a lieutenant in the Royal Engineers. He worked on the Rideau Canal in Canada and won the prized Telford silver medal for an essay on timbers. He returned to England in 1832 and was the first editor of Papers on Subjects Connected with the Duties of the Corps of Royal Engineers. He also instructed engineer cadets at Chatham where he set up an observatory, and later as an Admiralty officer he supervised the building and repair of dockyards and other works at Portsmouth, Woolwich and Bermuda. In November 1838 he married Caroline, daughter of Sir Phipps Hornby.
In April 1846 Gladstone dismissed Sir John Eardley-Wilmot from Van Diemen's Land and appointed Denison as lieutenant-governor. Earl Grey, who succeeded Gladstone, endorsed Denison's appointment and had him knighted. After five months in the Colonial Office Denison sailed from Spithead and reached Hobart Town on 25 January 1847.
In Van Diemen's Land, one of Denison's interests was education. In 1853 however, he had to agree to a bill which threw the cost of schools on the colonial Treasury and provided for the control of education by a board whose secretary was the inspector-general. One of Denison's last official actions was to commend a petition from the Legislative Council that the island's name be changed to Tasmania. The request was granted and took effect on 1 January 1856. On 13 September 1854 Denison had acknowledged the dispatch appointing him governor of New South Wales. On 9 December he received two commissions, each dated 20 September, one as governor of New South Wales, the other as 'Governor-General in and over all our Colonies of New South Wales, Van Diemen's Land, Victoria, South Australia and Western Australia'. He sailed with his family for Sydney on 13 January 1855.
As in Tasmania, Denison continued his interest in education. He was able to encourage the development of the infant University of Sydney and the Sydney Grammar School. He was also interested in engineering issues of the day. On 22 January 1861 he sailed to India to take up his new appointment as governor of the presidency of Madras. Denison's term in Madras ended in March 1866 and he returned to England by way of the Suez Canal which he examined and reported upon as an engineer. In 1868 he was appointed chairman of the inquiry into pollution of rivers in Britain. He gave many public lectures, some of which were published, and his eminently readable Varieties of Vice-Regal Life appeared in two volumes in 1870. He died at East Sheen, Surrey, on 19 January 1871. Lady Denison survived him until 1899.
Sydney Mechanics School of Arts (SMSA)
SMSA is the oldest operating School of Arts and operates the longest-running lending library in Australia. Since colonial times, the Sydney Mechanics School of Arts has made a major contribution to Sydney’s culture, industry, society and politics.
Governed by the Sydney Mechanics School of Arts Incorporation Act 1886, the SMSA is a self-funded not-for-profit organisation, wholly owned by its members. The Sydney Mechanics School of Arts was founded on 22 March 1833 at a public meeting attended by around 200 people. Among those present was Henry Carmichael who had first seen the need for a School of Arts in Sydney and spearheaded the movement, along with some of the artisans and tradesmen who had studied with him aboard the Stirling Castle during their voyage to Sydney. Major Thomas Mitchell, the surveyor general, was unanimously acclaimed as first President and Governor Bourke, an enthusiastic supporter, agreed to be first patron.
Schools of Arts and Mechanics Institutes came out of a progressive, forward-thinking movement that emerged in Scotland with the aim of providing open access to education for the working classes who were excluded from more formal and traditional education. It was quite revolutionary for the time. Whereas Schools of Arts concentrated on literature, history and the arts, Mechanics Institutes provided vocational training for mechanics who worked with their hands: skilled tradesmen like carpenters, bricklayers, stonemasons and blacksmiths.
The School quickly became the centre of colonial Sydney’s intellectual, cultural, social and political life. The members’ lending library provided valuable access to books, journals and newspapers; the talks and lectures were well attended; and various clubs and social activities kept members entertained.
Moreover, the School’s vocational education made a critical contribution to Sydney’s economic development, by fulfilling a desperate need for skilled labourers in the rapidly expanding colony. In 1878, the SMSA founded the Working Man’s College in a new building behind the main School of Arts. It was so successful that the Government pushed to take over and in 1883, the School accepted. It became Ultimo College and is a direct forebear of Technical and Further Education (TAFE) and both the University of New South Wales and the University of Technology, Sydney.
The SMSA has included among its members: NSW Premier William Holman, Prime Ministers Edmund Barton, George Reid and Billy Hughes and the Father of Federation, Sir Henry Parkes. Other famous members are explorer Ludwig Leichhardt, Edmund Hargraves, discoverer of gold in NSW and poets Henry Lawson and Henry Kendell.


Sydney Mechanics School of Arts (SMSA) : (left) 1856 sketch; (right) today from Google Street View.
The Lecture
SURVEYING - This is a word with which you are all familiar. Everyone who is possessed of property in land, or who has implanted in him those feelings (I may almost call them instinctive) which lead him to hope at some future time to be able to say, This land is my own, has a knowledge of the fact that the boundaries of that land must be somehow or other marked out for him. The process by which this is done is commonly called surveying. The more technical and descriptive term by which the art of the surveyor is defined is Geodesy, a term compounded of two Greek words - γη, the earth, and υαίω, to divide or portion out - and is descriptive of the actual work of the surveyor, whose business it is to map out or divide the surface of the earth, or rather of any given country, into portions of different sizes to suit the wants of its inhabitants.
This to some may appear a very simple process, especially when as in this country, the outlines of the different properties are generally straight lines; but the fact is that the work of the surveyor, if executed as it ought to be, involves an acquaintance with the results of the studies of the most acute intellects of ancient and modern times; and if executed ignorantly or improperly it gives rise to interminable litigation, of which we already have in this colony many examples, and shall probably have many more.
Geodesy, or the dividing the surface of the earth, has a distinct relation to geometry and geography. The first of those, which is compounded of the two Greek words - γη, the earth, and μιτριω, to measure - is the name of the science which teaches us how to measure the boundaries of the divisions, both great and small into which the surface of the country is cut up. The second or Geography, which is compounded of two Greek words - γη, the earth, and γραφω, to write or describe, teaches us how to describe, or rather to depict upon paper, the results of the work of the surveyor.
First then in order comes the science of geometry, without a knowledge of which the work of the surveyor must be most imperfectly performed. Next comes geodesy - that is the application of such science to the determination of the boundaries of any country, and to the division of it into portions of different sizes; and lastly comes geography, by which the determinations of the surveyor and the various lines which he has measured or calculated, are drawn in their proper relation to each other upon the maps which are intended to represent the country or portions of the country which has been subjected to measurement.
I have said that a knowledge of geometry is necessary to enable a surveyor to do his work properly; I do not of course mean that every surveyor must be an accomplished geometrician, but I do mean that he ought to have a competent acquaintance with the results of the mental toil of the geometer so far as these bear upon the work that he has to perform; he should have a knowledge of the mathematical rules or formula in which are considered, and made available for use, the results of years, I may say centuries, of intellectual labour; he should not only be acquainted with the rules but also with the mode of their application, in fact, this application is what is most essentially necessary to be known.
I might bring before you hundreds of instances in which the artizan or mechanic avails himself of the intellectual labour of the geometrician, without having an idea of the amount of mental toil which has been expended on the establishment of the principle which to him seems of all things the most simple; but I will content myself with one example of most familiar application, and yet one which has a very direct bearing upon my subject. The sempstress who wishes to cut a square piece of cloth from a long roll, the child who wishes to cut a square piece out of a sheet of paper - each will do so most easily by folding back one corner of such cloth or paper till the end of it is applied to, and coincides with the side; by marking then the point where the corner thus folded back meets the opposite side of the cloth or paper, and by drawing a line along the side of the article thus folded back, a square figure will be obtained as will be seen. I shall not attempt to particularise the variety of distinct propositions which have been combined to establish this simple process, each of which, though following in regular sequence, is by no means a self-evident consequence of that which precedes it; neither is it necessary that I should explain to you the limitation without a knowledge of which the experiment of constructing a square in the manner explained above, will fail; but as I have said that this simple process has an immediate bearing upon the subject of surveying, it may be right that I should point this out. You will see then that the fact of folding back one corner of the cloth or paper has the effect of making that corner into a triangle, and that the result is to show that a square is composed of two triangles, exactly similar and equal to each other. It is this construction of triangles which connects the experiment with surveying, for the branch of mathematics upon which the surveyor must depend is that which deals with and defines the relations between the different parts of triangles, and which is from thence called Trigonometry, from the Greek words τρίγωνον, a triangle, and μιτριω, to measure. I could not, of course, in a lecture like this, enter into any detailed explanation of the mode in which the relations of the parts of the abstract triangle are made to bear upon the actual measurement of the surveyor; I think, however, that I shall not waste your time if I linger a little in bringing before you some of the qualities of the triangle which have rendered it so applicable to the work of the surveyor.
A triangle is, then, as its name denotes, a figure having three angles, and necessarily, therefore, three sides. But its valuable quality is the invariable relation which exists between its parts and the permanency of its figure. Take the three sides of a triangle, and connect them together with pins about which motion might take place, yet the whole triangle remains fixed, none of its parts can alter; each angle and each side remain invariable. Take a square, or a figure of any number of sides exceeding three, and connect the sides of the figure in the same manner as those of the triangle are connected, although there will always be a figure having a given number of sides and also the same number of angles, yet this figure will be infinitely variable in form and dimensions, unless the points or angles of it are so connected as to divide it into triangles. This once done, the figure assumes the stability of the triangle itself - in fact the triangle being the figure composed of the fewest numbers of sides which can enclose an area, all other figures whose boundaries are straight lines may be considered as built up of triangles. I do not know that I can give you a more familiar illustration of the stability of form which belongs to a triangle, than by instancing the framing of a roof. If the rafters of the roof are made to rest upon the walls without any tie-beam - that is without the completion of the triangle - their tendency is to press the wall outwards, and this is the reason why in the old roofs of Gothic halls buttresses are added to the walls, in order to increase their stability and to enable them to resist the thrust of the rafters. The beam which connects the ends of the rafters is called a tie-beam, because a rope or chain or any connection which would prevent the spread of the feet of the rafter would answer this particular purpose as well as a beam. This invariability of form is a matter of the utmost importance; if, for instance, I measure the three sides of a triangle and ascertain their length, I have at once, by a simple calculation, the exact contents of the figure; but if the figure has four sides, such as those which mark nearly in every case the allotments of land in this and other colonies, then the knowledge of the length of these sides is, I may say, no guide to the area of the block of land enclosed by them. Take, for instance, this figure; it has four equal sides, each of which is, say 20 inches long, make a square of it by setting one side at right angles to the other, and the content will be 400 square inches; but let the sides alter their position with regard to each other, still keeping their length the same, and the area enclosed may be reduced to any extent; unite two of the angles of this four-sided figure by a diagonal line or tie - that is, make it into two triangles - and the area becomes invariable, as in the case of the single triangle.
I have detained you for some time in discussing this prefatory matter, but I think that from what I have said, you will arrive at a far clearer idea of the reason of many of the processes which I shall have to describe in the remainder of this lecture.
The survey of a country is, then, the process by which that country is divided into such parts as may be required for the various purposes of its inhabitants. There are large territorial divisions, as districts, counties, etc., for political or municipal purposes; there are subdivisions of these, as hundreds and parishes for purposes more local and particular; and there are, finally, the divisions which mark the property of individual inhabitants. Now the usual process has been, in newly settled countries, to begin with the third of these; to mark off the properties of individuals in the crudest and simplest manner possible, and then gradually, as the wants of society appeared to call for it, to aggregate a certain number of those allotments to form a parish, then a certain number of parishes to form a hundred, so many hundreds a county, so many counties a district, and so on. Now certainly, with regard to the first process, namely, that of marking off individual allotments, it must of course be done at once, and with such means as are in possession of the original settlers; but the evil of the system is, that this is not looked upon as a mere expedient, adopted to meet a temporary emergency, but is continued long after the original necessity has passed away. The crude processes, which were quite sufficient in the infancy of a society, are still kept in operation when the relations of the individuals composing that society have become complicated, and the consequences which result from such a miserable mistake are such as tend to create dissension, quarrels, and litigation between individuals, and to check the development of the resources of the country. I need hardly, I think, go into any proof of the assertion that the uncertainty of the boundaries of property does induce quarrels and litigation between neighbours; but perhaps the correctness of my second assertion may not be quite so evident; but when it is recollected that the settlers in a country as they arrive do not build their allotments one upon another like bricks in a wall, but that each man seeks for himself, when not prevented by some special impediment, such a location as may in his opinion suit his own feelings and habits, and that roads have to be laid out to provide access to different parts of a country upon some fixed system, I think you will agree with me that a little time and consideration expended in preliminary arrangements and surveys upon a proper system would not be wasted, but would, on the contrary, materially assist in developing the resources of the country.
What, then, is the course which ought to be followed when it is proposed to commence the survey of a country? Experience has shown that the only mode in which correct results can be obtained is to do that which you would perhaps infer from what has been said - namely, to divide it into a series of triangles of such dimensions as the nature of the country will admit of, - to subdivide these into smaller triangles; having thus determined a large number of fixed points throughout the country, the subdivision of these smaller triangles into allotments of any size or figure becomes an easy process, and, what is better, a sure and certain one.
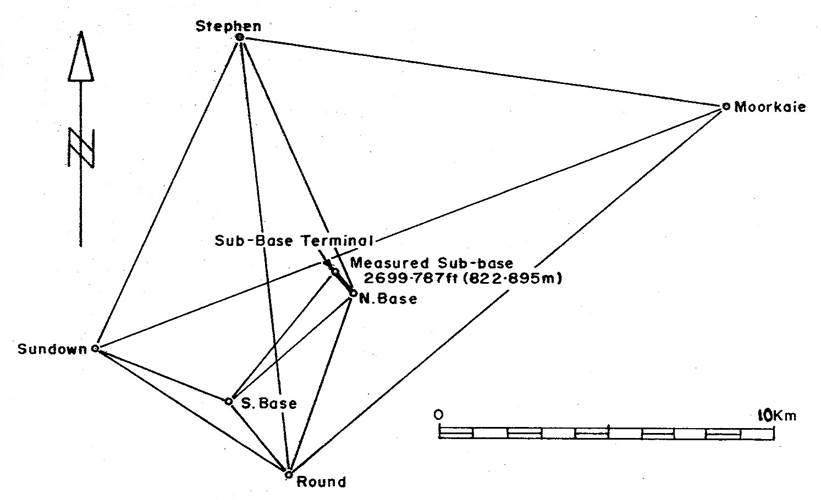
An example of triangulation from a base line.
But some may ask, how is it possible to divide a great extent of country into triangles? - and must we wait till this division has been made before we can get our allotments surveyed? To the first question I will reply by describing the process; to the second I say, by no means. All that is required is the determination of the sides of one triangle, to the fixed angles of which the lines of the boundaries of properties may be referred, and upon this triangle the whole survey of a country may be based. The process then, of triangulating a country is as follows :
On ground as nearly level as possible, a base line is measured with every possible care. The larger such line can be made the better, but from three to five miles is sufficient for all the ordinary purposes of an extended survey; from the two ends of this base, angles are taken by instruments invented for this purpose to the point determined and marked as the apex of the first triangle, this should be situated on some commanding ground from which the country round may be visible, and as from the data afforded by the measurement of the base and the observation of the angles it is possible to calculate the length of the other sides of the triangle, it is evident that upon the single foundation of one accurately measured line it is possible to cover the whole country with a network of triangles, to determine the position, with relation to the original base, of every remarkable feature, every hill, every house, every church, and thus to construct by the observation of angles and by computation, a foundation upon which all detached surveys of properties may safely rest. This may not perhaps be quite clear, but you will see that if, by having the side AB of the triangle ABC measured, and the angles A, B, and C observed, I can calculate the length of the sides AC and BC. I can then, in the triangle BCD having the side BC given by calculation and the angles observed, determine the sides BD and CD, and so on to any extent.
This process, which is the preliminary one in every accurate survey, is called the triangulation of the country; by it, as I said before, the position of every remarkable object can be fixed and determined, with a comparatively trifling amount of labour and with perfect accuracy; while if we have to depend upon the data furnished by ordinary measurements with the chain, any amount of error may be made in both the direction and distance of different remarkable points, which, though easily detected when a small amount of scientific observation has been bestowed upon the subject will probably have done an immense amount of evil by inducing all sorts of mistakes in the boundaries of properties, which will lead, if not checked by proper means, to an interminable amount of litigation. I have said that the position of different objects can be determined with perfect accuracy, by this of course I mean within very narrow limits; but a short account of what has been done will show you that these limits are very much narrower than you can have any idea of. I have said that the survey commences by the measurement of a base line of some three to five miles in length, from this angles are taken to different objects, and after the triangulation has been carried over a certain extent of country, it is usual to measure what is termed a base of verification, that is a new base, the length of which being determined both by computation from the original base and by actual measurement, a comparison of the two results serves to verify the correctness of the intermediate triangulation. In Van Diemen's Land, the bases were measured by wooden bars carefully prepared. The original base was some 20,000 feet in length, and a series of 12 or 13 triangles connected this with a base of verification distant about 80 miles from it. The intermediate angles were observed with a 12-inch theodolite mount upon a repeating table, and the difference between the measured length of the base of verification, which was rather longer than the original base, and its length was computed from the triangulation, did not exceed eight and a half inches, so that the positions of the different objects determined by angles taken with an instrument even so small as that employed in Van Diemen's Land may be considered for all practical purposes as fixed and, if properly marked on the ground, may from henceforward be referred to for all future surveys.
Thus, by a simple and a comparatively inexpensive process, data perfectly accurate can be obtained upon which to base the surveys for either roads and railroads or other public purposes, or for determining the properties of individuals. In every district there will be within a few miles, points whose position are fixed both absolutely and relatively. Absolutely, I mean, with reference to the surface of the globe - that is, where longitude and latitude are known. Relatively, with regard to other known points in the surrounding country. The distance, too, between those points is a fixed and known quantity, and thus each local surveyor, having at his disposal such elements of exactness, will be deprived of all excuse should he make any mistakes in his surveys and I may also say, that such mistakes will be very easily detected in the office of the Surveyor-General. The system of triangulation should of course be carried out even in the surveys of properties, if possible; but where the country is covered with trees, this may in many cases be impracticable. In such cases the benefit will be great if, having fixed points of reference in the stations and other points previously determined, to these the directions of the lines bounding properties may be referred instead of, as at present, to the ever fluctuating magnetic pole; any error which may creep in will probably soon be detected, and it will never, at all events be made the foundation of others.
From what has been said of the mode of proceeding with the triangulation of a country, it will be evident that the accuracy of the work must depend entirely upon the care taken in measuring the original base line; an error in the length of this line is reproduced and multiplied in that of the sides of the triangles computed from it. Many different methods have been adopted for the measurement of these bases, iron and steel chains, wooden rods, glass rods, bars of different metals arranged in such a manner as that the expansion or contraction of one should compensate or neutralise the expansion or contraction of the other, so as to keep two points in the line connecting the two bars, at the same invariable distance apart. Very accurate results have been obtained with all these various instruments, but I should be disposed, in a country like this, where the atmosphere though it has a great range of temperature, is generally dry, to use the simplest instrument - namely, wooden bars. These when properly prepared are less susceptible of expansion or contraction under changes of temperature than either metals or glass, and although the rate of expansion for increase of temperature has been determined by numerous experiments for these substances, yet there are many difficulties in applying such corrections, to which it is not necessary now to allude, and which it is as well to avoid if possible by the use of a material which is but little influenced by mere change of temperature. Wood, it is true, is acted upon by moisture, and is therefore affected by changes in the hygrometric state of the atmosphere - to this metals are not liable; but in this country by watching opportunities, measurements might be made while the atmosphere was dry - and besides this it is possible to guard against the action of moisture by careful preparation of the wood, while it is impossible to neutralise the action of heat. The instruments used for measuring a base require constant verification. They should he compared with a standard measure daily, and proper allowance made for any difference shown either in excess or defect. The measurement of each base should also be repeated two or three times in order to diminish the chances of error. When all these precautions are taken, which after all only require a little care and attention, the base may be considered as correctly determined, and the distance between the different stations, all of which depend upon the accuracy of the mean of various measurements of the base, may be safely depended on. The observations of the angles of the different triangles, the other element in the calculations, are subjected to too many checks to allow of any perceptible amount of error in them. The instruments which are commonly employed for the measurement of these angles by English surveyors are theodolites, of which I put before you one or two specimens.
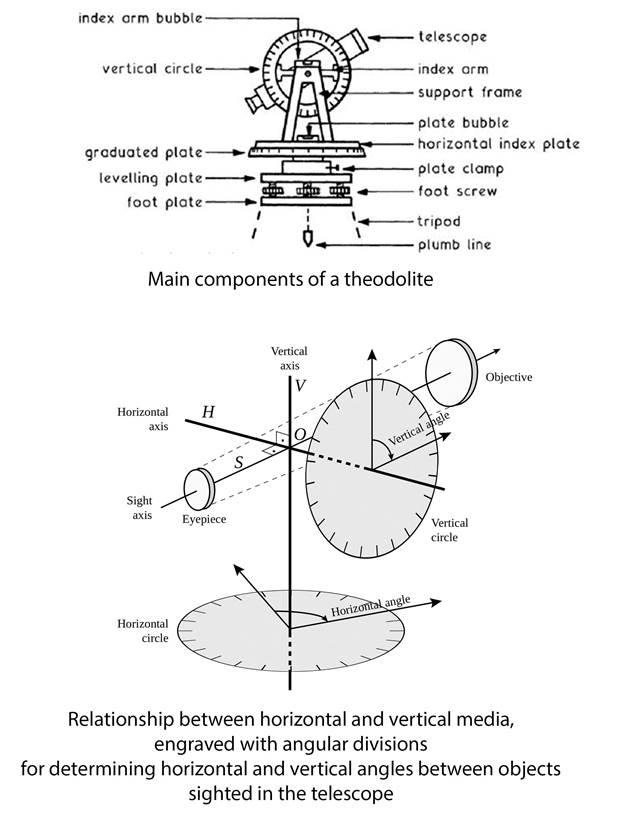
Overview of a theodolite
A theodolite is, as you will see, composed of a circular plate of metal, which being screwed down upon a stand supported by three legs can be afterwards adjusted by screws in a horizontal position, the accuracy of which is determined by a pair of levels at right angles to each other; upon this plate, the edge of which is divided carefully into degrees and portions of degrees, another circular plate traverses round the common centre of both, and this upper plate carries with it, first the telescope, the axis of which is defined by cross wires, and second, a circle, or a portion of a circular frame attached to the telescope or moving on the same centre. This upper one is used for the purpose of taking the angles of elevation and depression, by which the altitude of one station above another can be calculated while the lower horizontal limb indicates the horizontal angles or those subtended by different stations at the particular spot over which the centre of the instrument is fixed.
I have not attempted to enter into any detailed explanation of the construction, adjustments, and mode of using the theodolite. What I have said, together with the view of the instrument now before you, will be sufficient to enable you to understand the principle upon which it acts. The theodolites which are used for determining the angles of the larger triangle are much larger than this upon the table. Those used in England were three feet in diameter [and weighed some 100 kilograms], that is, the circle upon which the horizontal angles were read was of that diameter. In such a country as this, however, the difficulty of moving, and the risk of accident to, such an instrument would be too great to admit of its being used, and as an amount of accuracy quite adequate to our wants would be obtained by an instrument of eighteen inches diameter, which might be furnished with the means of repeating the observations and reading on various parts of the limb, it would not be wise to incur the expense and risk of purchasing a larger instrument.
Example of the 1791 theodolite made by Jesse Ramsden as used on the Principle Triangulation of Great Britain and Ireland, 1792, with a diameter of three feet and weighing some 100 kilograms (courtesy Science Museum Group Collection).
By observing then the angles subtended at each station by all the other stations within sight, and also by all marked objects of every description, and by recording the angles of elevation and depression, as shown on the vertical limb, the surveyor has it in his power to calculate the horizontal distances of these different objects from one another, and so, by degrees, to mark down upon the plan, or rather upon the paper prepared to receive the plan, a variety of dots or marks indicating the exact position of so many well-known places – the more these can be multiplied the easier will the work of future surveyors be, and therefore no remarkable object should ever be omitted in the round of angles taken from each station. It may be that an object, such as a remarkable tree or rock, or a bend of a river, etc. etc., may not be visible from other stations, in which case its exact position cannot be obtained - but at all events the single observation determines its direction, and forms thus a limit beyond which it cannot pass.
I feel that I have been led into greater detail than I at first intended, and were I to dilate as I might do upon the various precautions used to obtain accuracy and to insure the detection of error, this lecture would be lengthened into a treatise. I will therefore say briefly that the principle upon which surveys should be conducted is that of working from without inwards. The large triangle is first laid down with every possible accuracy, and the subordinate parts, the details of the division the ground within it, follow easily and correctly, as a consequence of the care bestowed upon the determination of the external limits.
The system hitherto followed in this and in many other colonies is precisely the reverse, that is, the small subdivisions of ground are measured without any pretensions to accuracy, one lot is built upon another to which reference is made in the descriptions attached to the grants of land. Every error, either of direction or of length, is perpetuated, - and as these detached surveys proceed from many distinct centres, the relation of which centres to each other can only be determined by inaccurate methods, it is not to be wondered at that when these detached surveys approach each other the most absurd mistakes are made. I have known a promise made of a grant of land on a particular spot, upon the faith of the correctness of the plan in the office of the Surveyor-General, which showed an available space between two contiguous surveys, proceeding from different centres of several hundred acres; but when it was necessary to mark out the land, it was found that the promised grant swallowed up a Government reserve upon which a signal station was built, and also half of the land already granted to the neighbouring settler. I mention this as an instance of the mistakes likely to arise from the system of working from within, outwards instead of from without, inwards. There are other mistakes which arise from the use of improper instruments, from carelessness in the measurements, etc., all of which are productive of great and lasting evils, and which under the present system cannot be detected; while, by the adoption of the well known and proper system of which I have given you an outline, every mistake not only can be detected in the office of the Surveyor-General, but in point of fact must be detected.
I have in my previous remarks confined myself to those questions which bear upon geodesy, that is, the division of land. I will, before I conclude, say a few words on the subject of geography. This term in its extended and more common application means, as you know, the description of the relative positions of different countries, and of the physical features of each, and of their political and social divisions. In the narrower sense, however, in which I am now using it, it means the art of depicting upon paper these physical and political features, and as the relative positions and outlines of these must first have been determined by the Surveyor, it appears to me that this lecture would hardly be complete without some allusion to the mode in which the work of the surveyor is presented to you in maps and plans. Now, the difference between a map and a plan is, I may say, twofold, - a plan is the picture on a large scale of the different features comprised in a small or comparatively small area; a map is a general view of a large area on a small scale, in which a vast variety of detail is necessarily omitted.
A plan again represents the position of the country embraced in it on a plane surface, and no perceptible error can arise from treating it as such. In a map, on the contrary, which is intended as a representation of the surface of a large extent of country, the fact of the general convexity of the surface of the earth cannot be left unconsidered. In looking at maps, I have no doubt that many of you have been struck with the presence of the lines which run from bottom to top, and of others which cross the map transversely, - the former representing the meridians, that is, the great circles which, drawn on the surface of the globe from pole to pole, pass through different places; these, however, on a globe, all converge at the poles, and a degree of longitude, or one 360th part of the circumference of the globe, at the equator being about 70 miles in length, becomes at the pole to zero. It does not, of course, make this change at once, but diminishes gradually from the equator to the pole. In maps, however, these meridians, instead of converging, are drawn parallel to each other, - and therefore when any extent of country in a high latitude has to be shown on a map, this parallelism of the meridians is apt to lead to a mistaken idea of the actual magnitude of the country thereon portrayed. The lines which cross a map from one side to another are the parallels of latitude, that is, lines intended to mark the number of degrees from the equator to the pole, and which are all parallel to the equator. The degrees of latitude may be taken practically as equal from the equator to the pole, and the lines on the map marking intervals of equal numbers of degrees, ought, one would be tempted to imagine, to be therefore at equal distances apart; if this, however, were the case, the relation between the distances measured on the meridians and those measured at right angles to it on the parallel of latitude would be constantly varying. In order, therefore, to allow the same scale to apply to the distance of one point from another, whether measured on the meridian or on a parallel of latitude, it is necessary that the increase in the length of the degree of latitude as shown on the map, should be in proportion to that of the degree of longitude. Here, again, the knowledge of the geometrician comes into play - he, it is, who furnishes the principles upon which these computations are made, and without the help furnished by him no map of any large district of country could be depended upon.
The conclusion which I wish you to draw from what I have read, is that surveying is not a mere empirical art, the practice of which can be taught in a few months to any man who has the usual allowance of brains, but that it is an art requiring for its proper performance, a large amount of acquaintance with mathematical science, in addition to a thorough system of practical training which can only be acquired by a species of apprenticeship under competent instructors during one or two years of regular employment. They, therefore, among you, who contemplate adopting the profession of surveyors, should begin without delay to lay the foundation of theoretical knowledge, without which you can never hope to be able to do your work effectually.
I trust that none among you would be satisfied with an amount of proficiency which might just enable you to escape blame. Believe me, that he who complies with the rule laid down by Solomon, Whatever thy hand flndeth to do, do it with all thy might, has not only the best chance of success in whatever he undertakes, but is sure to carry with him the respect and esteem of all who know him, and, what is of infinitely more importance, the testimony of his own conscience that he has done his duty.
Let me, therefore, avail myself of this opportunity to press upon all the observance of the advice given by Solomon; his rule is of universal application, and be assured that in following it we shall consult not only our interest, but our happiness.
W. DENISON.
Compiled by Paul Wise, January 2019, with thanks to Laurie McLean for finding the article.
Sources
Currey, CH (1972), Denison, Sir William Thomas (1804–1871), Australian Dictionary of Biography, National Centre of Biography, Australian National University, accessed at : http://adb.anu.edu.au/biography/denison-sir-william-thomas-3394
Science Museum Group Collection (2016), Theodolite by Ramsden 1791, The Board of Trustees of the Science Museum, Great Britain, accessed at : http://collection.sciencemuseum.org.uk/objects/co52825/theodolite-used-for-the-principal-triangulation-of-great-britain-theodolite
Sydney Mechanics School of Arts (SMSA) (2019), Sydney Mechanics School of Arts website, accessed at : https://smsa.org.au/about/
The Empire (1857), Denison on Land Surveying, Newspaper of Sydney, New South Wales, 1850-1875, of Wednesday 2 September 1857, pp.3, accessed at : https://trove.nla.gov.au/newspaper/article/64986130
