Baselines for Geodetic Triangulation Surveys in Australia

 

 

Compiled by Paul Wise, August 2021

 

 

Introduction

The successful early settlement of Australia depended on the release of land to new settlers. This posed a problem for successive colonial administrations as land released without a prior survey was quick but ended up later in litigation when many landholders found they owned overlapping properties. A prior survey meant that land release was delayed in the short term but ultimately meant peace of mind for landholders. It took some forty years and the arrival in 1827 of then Major (later Sir) Thomas Livingstone Mitchell (1792-1855) as Surveyor General that any systematic surveying and mapping of the new land of Australia was commenced. In fact, towards the end of Mitchell’s management he was able to say that due to the extensiveness of his surveys, any land sold since 1831 had been measured and mapped in its true place. Please refer to Figure 1 below which shows the areas discovered in Australia as at 1832.

 

Figure 1 : 1832 Map of the discoveries in Australia : copied from the latest M.S. Surveys in the Colonial Office / by permission dedicated to the Right Honourable. Viscount Goderich, H.M., principal Secretary of State for the Colonies, and President of the Royal Geographical Society, by his Lordship's obliged servant J. Arrowsmith [Arrowsmith, John, 1790-1873]

(courtesy National Library of Australia, nla.obj-231944045).

 

Triangulation

By this time, survey by triangulation had become the accepted method of establishing points of known coordinates in the terrain which could be used for mapping and the determination of individual property boundaries. Generally high points in the terrain were chosen to form a series of triangles, hence Triangulation. The internal angles of these triangles would then be observed with optical instruments of the day. Knowing that the angles of each triangle had to equal 180 degrees allowed a check to be kept on the quality of the angle observations (over large areas the curvature of the Earth meant that the angles of a triangle actually added up to more than 180 degrees but this spherical excess could be calculated so as to still maintain a check on the angular observations). To provide scale for a triangulation survey at least the side of a triangle near the start of the survey was measured and another near the end. Using the measured length of the first side of a triangle, all the sides of the triangles were then calculated and the calculated length then compared with the measured length near the end of the survey. The misclose between the measured and calculated length then provided an overall check on the triangulation’s accuracy. As the extent of a triangulation survey grew, further sides of triangles were required to be measured so any errors could be quickly isolated.

 

In practice the difficulty arose in that the angular observations had to be taken on high points to have visibility over the intervening ground. Measuring a triangle’s side with the equipment of the day, however, up and down significant slopes did not achieve an accurate length for a triangle’s side. Thus, rarely was the side of an actual triangle measured. Instead the solution was to find a relatively flat piece of ground from which high points in the terrain could be seen and from which the triangulation proper could commence. On this flat terrain a baseline was prepared and very accurately measured and from the terminals of the baseline angles were observed to points in the triangulation proper. This configuration was known as a basenet. Please refer to Figure 2 to see an indicative basenet, where points Trig 1 to 4 are on high points and part of the required triangulation, whereas the points Base north and Base south are on a plain with visibility to some of the surrounding high points of the triangulation as shown. With the necessary angular observations taken to all visible points and the distance Base north-Base south known by accurate measurement, the distances Base south-Trig 3 and Base north-Trig 3 could be calculated. In turn triangle sides Base north-Trig 4 and Trig 3 to Trig 4 and sides Base south-Trig 1 and Trig 3-Trig 1 could then be calculated. The remaining sides of the triangles of the triangulation proper could now be calculated progressively.

 

Figure 2 : Indicative basenet; angles to visible points in the triangulation from the baseline terminals allowed the sides of the main triangles to be calculated.

 

The use of triangulation in surveying came from the work by Dutch mathematician Willebrord Snell. Willebrord Snellius, born Willebrord Snel van Royen (1580-1626) was a Dutch astronomer and mathematician, known in the English speaking world as Snell. Snell in 1615 surveyed the distance from Alkmaar to Bergen-op-Zoom with a chain of triangles controlled by a baseline at the start and two check baselines at the end. Snell, however, appears to have been influenced by the earlier work of Gemma Frisius (1508-1555) and Tycho Brahe (1546-1601) dating back to the late 1500s. Between 1733 and 1740 Jacques Cassini (1677-1756) and his son Cesar Francois Cassini de Thury (1714-1784), also called Cassini III or Cassini de Thury undertook the first triangulation of the whole of France. Their work subsequently led to the publication in 1745 of the first map of France constructed on rigorous mathematical principles.

 

In 1785 Cassini de Thury proposed the French and English cooperate in a survey to determine an arc of parallel between the longitudes of Greenwich and Paris. The English survey was placed under the control of then General William Roy (1726-1790) founder of the Ordnance Survey in 1791, and the French survey under Dominique comte de Cassini (1748-1845), son of Cesar Francois Cassini de Thury, Pierre Francois Andre Mechain (1744-1804) and Adrien Marie Legendre (1752-1833). The triangulation network ran from London to Dover across to Calais joining with the existing French triangulation near Dunkirk to Paris. This achievement led to a geodetic survey of the United Kingdom by triangulation. The Great Trigonometrical Survey of India, as it became known, started on 10 April 1802 with the measurement of a baseline near Madras, now Chennai. Then Major William Lambton (c1753-1823) selected the flat plains with Saint Thomas Mount at the north end and Perumbauk Hill at the southern end for a baseline of 7.5 miles (about 12 kilometres). The Indian triangulation was not completed for another seventy years.

 

The triangulation baselines for these, and all later triangulation surveys, were thus measured with the highest possible accuracy of the day. Special wooden bars, steel rods, and steel bands were finally replaced with Invar bands (Invar is a nickel-steel alloy invented by Swiss physicist and metrologist Charles Édouard Guillaume in 1896. It was named Invar for its Invariability under extremes of heat or cold; its coefficient of expansion is 15 times less than that of steel. Guillaume was awarded the Nobel Prize for Physics in 1920 in recognition of the service he has rendered to precision measurements in physics by his discovery of anomalies in nickel steel alloys). In the early 1900s an Invar band’s calibration was given to be the equivalent of 1 millimetre in 1 kilometre (one part in 1 000 000) at temperatures from 5° to 40°C.

 

For the baseline for the triangulation of Ireland, Thomas Frederick Colby (1784-1852), devised a dual arrangement of brass and iron, which he called a compensation bar. The Colby compensation bar or just Colby bar, as his apparatus became known, was used for baseline measurements in all parts of the world, but were relatively expensive. Colby clamped together a bar of brass and a bar of iron both about 10 feet long. The central clamping meant any expansion/contraction of the materials due to temperature would occur at the extremities of the materials. As the two materials reacted differently to any expansion/contraction he was able to devise a method where two positions on the combined bars always remained 10 feet apart despite nominal temperature changes.

 

The National Mapping Office in 1953, produced on behalf of the National Mapping Council, Standard Specifications for Horizontal and Vertical Control. At this time, as triangulation was still the dominant survey method in Australia, these specifications provided an insight into the accepted Australian standards for such surveys. Of note was the following :

 

-	chains of triangulation shall not normally exceed 200 miles (300 kilometres) in length between baselines;
-	baselines shall be measured with an accuracy represented by a probable error not exceeding 1 part in 1 000 000 (1 millimetre in one kilometre) and an estimated actual error not exceeding 1 part in 300 000 (1 millimetre in 300 metres); and
-	chains of triangulation shall be so designed and executed, that after the side and angle equations have been satisfied, the probable error of the length obtained for the closing base, when computed from the starting base as an ordinary side of the triangulation shall not exceed 1 part in 100 000 (1 millimetre in 100 metres) and the actual discrepancy between the computed value and the measured value of the closing base shall not exceed 1 part in 25 000 (1 millimetre in 25 metres).

 

In practice, however, finding a suitable site for a baseline along the route of the triangulation every 200 miles or so, was not always possible. It would seem then that this clause was read as being more of a desirable feature of a triangulation survey rather than a mandatory requirement.

 

 

 

Triangulation Baseline Measuring Apparatus

 

-      early Australian linear standards

A Surveyor’s or Gunter’s chain was probably the first linear standard in Australia. The chain made of thick steel wire, consisting of 100 main links connected together by about 300 smaller rings, was invented by Edmund Gunter (1581-1626). From about 1620 the Gunter’s chain became the instrument for distance measuring in Britain, with a length equivalent to 22 yards or 66 feet; ten chains were a furlong and 80 chains a mile. Gunter's chain then integrated two seemingly incompatible systems; the traditional English land measurements, based on the number four, and decimals based on the number 10. Since an acre measured 10 square chains (or 100 000 square links) in Gunter's system, the entire process of land measurement could be computed using measurements in links, and then converted to acres by dividing the results by 100 000. The Gunter’s or Surveyor’s chain was different from an Engineer’s chain which had a length of 100 feet.

 

A Gunter’s chain would have been among the equipment bought to Australia by the First Fleet in 1788 for use by Australia’s first Surveyor General, Augustus Theodore Henry Alt (1731-1815). (As the Gunter’s chain construction made it prone to distortion over time it was probable that more than one such chain was landed; at least one working chain and one other chain kept theoretically pristine to be used to periodically standardise the working chain). In May 1787, Alt had been appointed surveyor of lands for the new colony of New South Wales. In late 1791 because of ill health, Alt asked to be replaced as Surveyor General. Then Governor Arthur Phillip supported his request, and while waiting for a replacement employed Lieutenant William Dawes and David Burton to survey settlers’ farms. Lieutenant Governor Francis Grose subsequently ordered Charles Grimes to Sydney to act as deputy surveyor general in 1794. Grimes virtually performed the work of Alt, until 1803 when he finally replaced Alt as Surveyor General and in turn in 1827, Thomas Livingstone Mitchell became Surveyor General.

 

It was not until 24 August 1832, however, that An Act (designated 3 William IV, No.4) for establishing Standard Weights and Measures, and for preventing the use of such as are false and deficient, determined that : Whereas it is necessary to provide against the use of fraudulent weights and measures in New South Wales and its dependencies, and for that purpose to establish certain standards by which all other weights and measures may be regulated, and to prohibit the use of any other weights and measures than such as shall agree with such standards; and whereas certain weights and measures of the standard now in force and in use in the United Kingdom of Great Britain and Ireland, denominated Imperial Weights and Measures, (a schedule whereof, marked with the letter A, is hereunto annexed,) have been deposited in the Colonial Treasury, in the town of Sydney. Be it therefore enacted by His Excellency the Governor of New South Wales, with the advice of the Legislative Council thereof, that the said several Weights and Measures now deposited in the Colonial Treasury, in Sydney, as aforesaid, shall be there safely kept, and shall be, and they are hereby declared to be, the Standard Weights and Measures of New South Wales [the schedule marked with the letter A mentioned above, listed as the Standard Measures of Length; One Yard, One Foot, One Inch]. A standard set of imperial weights and measures included a standard yard (approximately 1 metre).

 

By 1848, in New South Wales, their standard yard had been used to establish a baseline for the calibration of Gunter’s chains then in use in that colony. More specifically a standard of 100 links...established by cutting marks in the stone flagging in front of the old Lands and Survey Office in Bridge Street, Sydney, which according to one authority, was probably correct to within half an inch or so, was prescribed in 1864 to be used for the official calibration of Gunter’s chains.

 

Steel bands replaced the chains in the 1880s. While more rugged than the chain the growth of cities and towns required a consistency of measurement necessitating steel band calibration facilities be more accurate and more widely available. With the adoption of steel measuring bands, a more rigorous approach to the definition of distance was now possible. While the Gunter’s chain had performed well, its vagaries in producing consistent results could no longer be tolerated. Land, especially in the cities, was now becoming too expensive to be defined by approximation. Even though the stability of the steel band far exceeded that of the linked chain a repair or bad kink could still jeopardise its legitimate length.

 

Figure 3 : Sydney Observatory ‘Standard Measure’ or baseline

(after 1881 publication by the Government Astronomer H.C. Russell entitled ‘Results of Astronomical Observations made at Sydney Observatory – 1877 and 1878’ and held at the Mitchell Library).

 

Standards of 66 feet and 100 feet with stone terminals carrying the marks showing the distances had been laid down at Sydney Observatory around 1880 following the destruction of the one chain length in the pavement at the front of the Old Lands Office, Sydney. Figure 3 above shows the location of the Standard Measure in relation to the observatory. Although, of great service to surveyors generally…the observatory standards were apparently damaged by rough usage and were later found to be 0.04 inches [about 1 millimetre] short.

 

In June 1863, the Melbourne Observatory began operations following its move from its original site at Williamstown. A baseline of 100 feet was established nearby in 1882-83. The Victorian 10 foot standard OI6, discussed below, was used to set out the baseline to enable the Gunter’s/Surveyor’s 66 feet/100 link and Engineer’s 100 feet chains, to be accurately calibrated. Figure 28 below shows its location in relation to the Melbourne Observatory.

 

The first Intercolonial Conference of Surveyors in the southern hemisphere was convened in Melbourne on 31 October 1892. Among the outcomes was that the conference resolved to recommend that the measure of length used in all Australasian surveys being the English measure of length, as provided by English Statute law, standards 66 feet and 100 feet in length, in terms of such legal standard, should be established in the principal Australasian cities and adopted as the standard of surveys in all the colonies.

 

Nevertheless, other wooden or metallic linear standards were generally separately obtained for baseline measurement purposes.

 

-      brass and iron, steel and Invar to light and microwaves

In addition to his compensation bars, already described above, Thomas Colby also had two ten feet iron standard bars manufactured. These two bars were to serve as a permanent record of the length of the compensation bar and of the base measurements when undertaken at a temperature 62°F. Further, two three feet (1 yard) bars, were also manufactured.

 

When the Houses of Parliament in London, burnt down in 1834 the primary Imperial standard yard for England and its colonies was destroyed. Due to Colby's foresight in having copies of the standard made the primary Imperial standard yard was able to be re-established some ten years later. Thus in 1845, forty bars were cast and the one that best matched the length of the existing yard became the new Imperial Standard Yard. The next best bars were approved as Parliamentary Copies and sent to England's cities and colonies. Parliamentary Copy No.18 was received by the Colony of New South Wales, and likewise copy No.34 by the Colony of Victoria, in 1855. There is also reference to South Australia having a brass yard standard in 1840. The source of this standard is, however, unclear.

 

These yard standards, were used to standardise chains for local land titling and triangulation surveys but, as will be seen, it was the 10 feet standards that were the reference during the major early baseline measuring activities.

 

Sir Thomas Makdougall Brisbane (1773–1860), during his term as Governor of New South Wales from 1821 to 1825, established a private observatory at Parramatta. Later, in 1828, the observatory took delivery of the requisite rods and cylinders for the trigonometrical survey. This survey was for the determination of an arc of the meridian which never eventuated.

 

In April 1846, Sir William Thomas Denison (1804-1871) was appointed the Lieutenant Governor of Van Diemen's Land, today’s Tasmania, and resided in Hobart from 1847 to 1855. It was while in Tasmania he saw the use of wooden bars for baseline measurement for triangulation surveys, as in a public lecture in 1857, Dennison not only spoke of the Tasmanian work but also voiced the opinion that : in a country [now referring more broadly to Australia] like this, where the atmosphere though it has a great range of temperature, is generally dry, to use the simplest instrument - namely, wooden bars. This thinking was driven by the fact that although Colby bars were available, they were beyond the financial resources of any Colony to be acquired.

 

George Robarts Smalley (1822-1870), then Government Astronomer for New South Wales, refers to these same wooden bars in his published 1869 letter at Annexure A. In March, 1867, I proceeded to Melbourne…[and] was fortunate enough in recovering some well-seasoned pine bars belonging to the Government of New South Wales, and which appear to have been sent out some thirty years ago to the Government of Tasmania, and afterwards, through some mistake, deposited at the Lands Office, in Melbourne. As will be seen later, when used at Lake George during 1873-74, the thought to be now well seasoned wooden bars reportedly acted in a most incomprehensible manner. By now however, the iron standard was now available.

 

In December 1858 and March 1862, New South Wales and Victoria respectively received their 10 feet wrought iron standards. The standards were designated OI4 and OI6 (the numerical identifier 4 and 6 is often shown in literature as a suffix making it very hard to see in old documents; here the full size numeral will be used for clarity) respectively. The original 10 feet wrought iron standard, designated O1, was constructed for the United Kingdom Ordnance Survey in 1826-7. The manufacturer was the British instrument making firm, Troughton & Simms Company, formed when Edward Troughton in his old age took on William Simms as a partner in 1826. So as to keep their standard O1 pristine, and not only to be able to obtain the length of O1 in terms of the existing standard yard but also to provide a standard which had other markings for comparing with other international standards of the day, Ordnance Survey had another intermediate standard made which was designated OI1. The Australian wrought iron standard bars were copies of OI1, hence their designation as OI4 and OI6 (an OI2 was also made at that time and may have been eventually sent to Australia in 1881). The position of the markings on iron standards OI4 and OI6 is shown in Figure 4 below, with Figure 5 below showing a ten feet iron measuring rod from the period, belonging to the now State of Victoria.

 

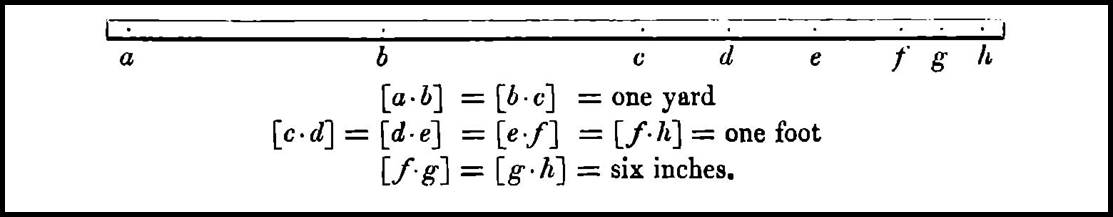
Figure 4 : The markings on iron standards OI4 and OI6 (after Clarke, 1866).

 

Other standard bars constructed for Ordnance Survey for comparison with other international units of measure, were the Ordnance Toise, designated OT, Ordnance Metre, designated OM, and Ordnance Foot, designated OF. Butterfield (1906), compiled the following table relating most of the common European measures (note that these values will vary with modern adopted national and international values of today) :

 

 

Figure 5 : Ten feet iron measuring rod (courtesy Museums Victoria).

 

Attention to detail, please refer to Figure 6 below, when measuring baselines with rods, meant that geodetic triangulation baselines were time consuming operations sometimes taking many months to complete. As engineering methodologies were refined whereby a thin strip (ribbon) of steel and later Invar could be manufactured, the heavier and cumbersome rods where replaced by these more portable and stable measuring apparatus for baseline measurement. With the improvement in the measuring technology, however, baselines were remeasured to ensure the most accurate results were derived for the survey. Errors arising from uncertainty in temperature measurement were always a concern – was the temperature given by the thermometer(s) that of the metallic band? After 1938 in Australia, such errors were greatly reduced by standardising the metallic measuring bands in terms of their electrical resistance instead of at a stated temperature. More on this resistance thermometry technique is available at Annexure B. Around that time, then Major Thomas Alexander Vance (1882-1959), officer commanding the Australian Survey Corps published a paper The Present Methods of the Australian Survey Corps. Among other topics, Vance’s paper described RA Survey’s approach to baselines to that time :

 

RA Survey aim at placing baselines about 200 to 250 miles apart and adjusting the triangulation in sections between baselines.

 

It is not easy to find a good base site. In addition to facilities for measurement, the base terminals must be intervisible and considerably elevated above the surrounding terrain, and an extension through well conditioned figures to the main triangles must be possible. It has been found by experience that it is more important to have good conditions for the angular work than it is to have a perfectly or nearly flat surface for the lineal measurement. Slopes up to 5° or 6° can be measured without a falling off in accuracy if proper precautions are taken. A convenient length for a baseline is from four to six miles.

 

Invar bands 330 feet [5 chain] by one-eighth inch wide are used. In the past these have been standardised by comparison with the 66 feet standard in the basement of the Lands Department, Sydney. It is well known that Invar bands have a tendency to alter in length as they age and during use. They have to be handled with great care, as they are easily kinked. They should be standardised immediately before and after the measurement of each base, and should be compared frequently with the field standard during the measurement. Probably the greatest error in the measurement of a baseline is due to the uncertainty of the length of the band. Owing to the difficulty and delay caused by frequently having to send the bands to Sydney for tests and to the value of the Sydney standard itself being open to criticism, the Survey Corps are importing four steel bands which are being standardised at the National Physics Laboratory, England. Steel bands are not suitable for measurements of precision, owing to their high coefficient of expansion, if the only control of their length is obtained by taking the temperature with thermometers. To overcome this disadvantage, we are using a new method whereby the bands are standardised in terms of their electrical resistance instead of in terms of temperature, the resistance of the bands being measured simultaneously with the comparison of their lengths. It is estimated that by this means they can be standardised to one part in one million, against one in 400,000 by the temperature method; and that their change in length corresponding to a difference of temperature of less than ½°F, can be measured under field conditions. It is not intended to use the steel bands in the actual measurement of the base, but to have a ready means of making frequent comparisons with the Invar field bands. Experience has also shown that the coefficient of expansion of Invar as supplied by the makers is not reliable. A band drawn from an ingot may have a different coefficient from another drawn from the same source. We found the actual value of two bands to be more than three times that given by the makers. It is necessary to determine, experimentally, the coefficient of each band.

 

The measurement proper is with the Invar band suspended in catenary. At least two measurements of the base must be made and if these do not agree within the specified limits, a third measurement would be necessary. The measurement must be suspended during windy or wet weather.

 

The working Invar band is compared [pre RA Survey’s adoption of the resistance thermometry technique] with the reference bands before and after each day's measurement. This can most conveniently be done on a temporary ground standard, established in a convenient position near the base. The bands to be compared are suspended side by side, in catenary and several comparisons are made.

 

Corrections that have to be applied to the base measurements are for grade, temperature, difference of scale readings, sag, deformation of catenary on slopes, variation from standard, and height above mean sea level.

 

Figure 6 : Baseline measurement by rods in America (courtesy Penry, 2019).

 

In the mid twentieth century, the ability to measure travel times of frequencies in the electromagnetic spectrum meant that the distance between two points could not only be measured accurately but the intervening terrain no longer had to be physically traversed with the measuring apparatus. Thus, not only could triangulation baselines be measured with such electronic equipment but eventually the portability of such equipment resulted in complex Triangulation being replaced by simple Traversing. The era of triangulation ended.

 

In May 1954, National Mapping received a Geodimeter (a name derived from GEOdetic DIstance METER) Model NASM-1, manufactured by AGA (Aktiebolaget Gasaccumulator) of Sweden. Today the term Electronic Distance Measuring (EDM) equipment covers any device that uses an electronic means to measure distance and the NASM-1 Geodimeter was not only an EDM instrument but in fact the first line-of-sight EDM instrument. The Geodimeter generated frequencies in the visible light region of the spectrum. While at the Nobel Institute of Physics in Stockholm, Sweden in the latter 1940s, Dr Erik Osten Bergstrand developed an instrument to measure the speed of light. In 1947, Bergstrand took his instrument to a 7 734 metre triangulation baseline, from the island of Lovö to Vårby near Stockholm, and obtained a measurement for the speed of light. With a value for that constant, Bergstrand now adapted his device to obtain the distance between any two intervisible points and later in 1953, the first commercial model of the Geodimeter, the NASM-1 emerged. After successful testing, in 1955 Nat Map now believed that with the Geodimeter available to measure the side of a triangle every 400 kilometres or so in the main triangulation network, there would no longer be a need for tedious baseline measurements, or the observing of the associated and time consuming basenet schemes. Almost immediately however, the arrival of the Tellurometer EDM in 1957 made triangulation obsolete. The Tellurometer generated frequencies in the microwave region of the spectrum. There is further discussion of EDM and its effects on triangulation later in this article.

 

 

 

Australian Triangulation Baselines 1827-1970

 

Preamble

The earliest triangulation baselines were established under Surveyor General Mitchell in the late 1820s and through the 1930s. In this era the only Australian colony was that of New South Wales. As is discussed later in the paper the colony of New South Wales recommenced its triangulation again in 1867. By this time however, other colonies had come into being. It was only Victoria that for a while adopted a different survey methodology but eventually, they too reverted to a survey by triangulation.

 

At the 1912, Conference of the Director of Commonwealth Lands and Surveys, the Surveyor-General and the Government Astronomer of New Zealand, and the Surveyors-General of the States of the Commonwealth of Australia, held in Melbourne, the Surveyors General each presented a review of their Colonial and now State survey activities to date. Several States declared that their triangulation activity was complete although it did not cover the whole of their State. The major reason was that the specific States had run out of hilltops and the plains/desert country was completely unsuitable for continuing with triangulation. In addition, much of such country was also unsuitable for settlement.

 

With a World War coming soon after the 1912 Conference and then a Depression there was an understandable lack of triangulation activity. Activity accelerated once again when World War Two demanded accurate surveys for strategic requirements. Post war development priorities then kept triangulation activity from slowing again. Thus, the discussion of the baselines for triangulation surveys in Australia has three parts; Triangulation Baselines of the 1830s being essentially the Mitchell era up to 1867 in New South Wales; Triangulation Baselines 1840-1912 being the triangulation work reported by the respective Surveyor’s General at the 1912 conference; Triangulation Baselines 1920s-1950s as documented in reports of the National Mapping Council and described in various sources.                                                                                    

 

Following this discussion, a summary of the baselines is tabled (even with best efforts this table may still be incomplete). All geographical coordinates quoted are on the Australian Geodetic Datum 1966 (AGD66) and are the best available based on the information obtainable about the location of the baseline and/or its terminal stations. The names of the terminal stations are spelt according to modern nomenclature. From the terminal coordinates the length of the baseline was calculated in metres (rounded to the nearest metre) using Vincenty’s formula and the AGD66 spheroidal parameters. The baseline distance in metres was then converted to miles (rounded to a tenth of a mile). Where only the length of a baseline was accurately reported this Imperial length is noted and converted to metres and miles.

 

In the pre 1912 era some baselines were measured with special apparatus others were not. Thus, unless the measuring apparatus used on a baseline was specifically mentioned the table lists the apparatus as Unspecified although in the text the probable measuring apparatus might be given, based on the era. In the case of the South Australian baselines it was known that the 66 feet/100 link Gunther’s chain was standard equipment. This knowledge meant that if the measuring apparatus used on a South Australian baseline was not mentioned it could rightly be assumed that a 66 feet/100 link chain was used. In the post 1912 era Invar bands were the norm, although information on the length and number of bands used was not always available. In the case of RA Survey, 5 chain (330 feet) Invar bands were used in the 1920s and 1930s, for their baseline measurements. Later during the war however, when second order standard work sufficed, it appears that more durable, 300 feet Steel bands were used. These two facts are thus reflected in the table. (Note that the word band is preferred instead of tape for describing the measuring apparatus as today the word tape describes a more flexible, general purpose, measuring apparatus, material.) The Reference numbers shown thus (NN) in the text refers to the numbers in the Reference column of the table.

 

Individuals who are mentioned as being involved with historical and mainly pre 1912 baselines are listed alphabetically at Annexure C. The list provides a link to where more detail on the individual, if available, may be found.  

 

In all the now major capital cities of Australia, and indeed many of the then isolated larger centres of population, the first triangulation surveys were only for town planning purposes so a single baseline was sufficient. It was only as the Colonies started to expand inland were the wider implications of a geodetic triangulation with adequate, highly accurate baselines considered. Please refer to Figure 7 below. It is these geodetic triangulation baselines that is the focus of the remainder of this article. Nevertheless, baselines used to control significant mapping surveys are discussed as appropriate.

 

It should also not be overlooked that the initial surveying and mapping of some of the larger islands of Australia also required the establishment of baselines. Of note were the baselines of Flinders Island, Tasmania; Montebello Island, Western Australia; Melville Island, Northern Territory and Long Island and Fraser Island, Queensland. Before being connected to the mainland two baselines were established to control the triangulation of Tasmania; at Longford, 25 kilometres south of Launceston and at Cambridge, 15 kilometres east of Hobart. It was also found that in 1890-91 a survey of Moreton Bay, where the whole coast line was traversed with theodolite and band, and the triangulation computed from a baseline 26 227 feet [some 5 miles or 8 kilometres] in length on Moreton Island. In undertaking their regional mapping responsibilities RA Survey also established baselines. Of note was the survey and mapping of New Britain where 19 third order baselines were measured with astrofixes for latitude, longitude and azimuth. (While not strictly correct RA Survey is used throughout to refer the Royal Australian Survey Corps or their predecessors.)

 

Figure 7 : (Centre) October 1967 photograph, courtesy of Andy Rodgers, of Klaus Leppert, Supervising Surveyor, Geodetic Branch, inspecting the Oxley Theodolite Memorial, commonly known as the Big or Giant Theodolite, erected at Booligal, New South Wales, as a memorial to Explorer and Surveyor General John Oxley, unveiled by Sir Eric Winslow Woodward KCMG, KCVO, CB, CBE, DSO (NSW Governor 1957-1965) on 8 August 1967, the simple plaque reads: Lieut. John Oxley, Surveyor General of NSW reached this point on 5th July 1817;

(Left) John Joseph William Molesworth Oxley (1784-1828, Mitchell’s predecessor as Surveyor General, 1812-1828);

(Right) More recent photograph of the Oxley Theodolite Memorial.

 

Triangulation Baselines pre 1912

 

New South Wales to 1867

As stated above it was then Major Thomas Livingstone Mitchell as Surveyor General that became the driving force behind the triangulation surveys in New South Wales. He and his colleagues left their legacy in not only today’s New South Wales but also today’s Queensland and Victoria. Unfortunately, some of those later involved with the results of these surveys were not impressed with Mitchell’s implementation. One was George Robarts Smalley (1822-1870), then Government Astronomer for New South Wales. In an 1869 letter, Base Line for the Triangulation of New South Wales, published in The Sydney Morning Herald newspaper, Smalley wrote…In measuring a baseline, it is of the greatest importance that in future generations someone should be able to verify it; yet this is rarely possible. I may instance…Sir Thomas Mitchell’s small baseline on the Botany Sands; also, his measured check line somewhere near Lake George. Please refer to Smalley’s published letter at Annexure A.

 

Later, Augustus Charles Gregory (1819-1905), the first Surveyor General in Queensland, recorded in 1885 that about 1850 Mitchell began a triangulation survey of Moreton Bay and the Darling Downs (it was actually Mitchell’s assistant surveyor Robert Dixon who did the actual work as is discussed below) : but the imperfections in the measurement of the baseline on the Normanby plains by the use of hardwood bars of ten-foot lengths, the small size of the theodolites, and somewhat unfavourable selection of the trigonometrical stations,…left the work in such an imperfect state as not to be of much value (Cumpston, 1954). In 1828 and 1829, Dixon had carried out triangulation in the Camden area and near the Murrumbidgee and Molonglo Rivers.

 

Nevertheless…The advent of Major Thomas Livingstone Mitchell…was to transform the department and the profession of surveying in Australia. Mitchell took in the department’s disarray at a glance. There was, he noted, ‘not a single theodolite in the colony that was fit for use’ and he at once set about repairing this accurate survey instrument with its clear line of sight for measuring horizontal and vertical angles. He also gained permission for making a trigonometrical survey of the colony (Moyal, 2017).

 

It would appear that Mitchell, while wanting to achieve a high quality survey, felt he did not have the time to meet all the requirements of such a survey. Time consuming and also expensive tasks like the monumenting of observation stations and baselines was thus avoided. On the most prominent of the visible hill/mountain tops he had all the vegetation cleared save for one conspicuous tree which was used as the target in his theodolite. This decision in no way impacted his survey’s quality but in time physical traces of those points disappeared diminishing his surveys future value; this was the point Smalley made in 1869 mentioned above.

 

Mitchell’s approach has been described as a reconnaissance type triangulation survey aimed at establishing survey control over an extensive region to produce a map correctly depicting the main terrain features. His expertise in such an approach to survey and mapping came initially from his 16 years of military service where he fought in the Peninsular War (the Peninsular War (1807/08-1814) described that phase of the Napoleonic Wars fought on the Iberian Peninsula, where the French were opposed by British, Spanish, and Portuguese forces, for control of the Iberian Peninsula, the peninsula in southwestern Europe, occupied by Spain and Portugal. Arthur Wellesley, 1st Duke of Wellington, KG, GCB, GCH, PC, FRS (1769-1852) was leader of the British force and eventually won against Napoleon at the Battle of Waterloo in 1815). Rightly or wrongly then, Mitchell’s survey work left no ground marks so only descriptive evidence exists as to its locations.

 

In his publication Thomas Mitchell : Surveyor General and Explorer, Cumpston  (1954) quoted part of a letter from Mitchell to his mother, dated 1 February 1828,…I measured a base of a mile on the smooth sandy beach at Botany Bay yesterday for the purpose of making a grand survey of the whole country...I came, as it were, accidentally on a brass plate fixed in the rock marking the first spot where Captain Cook had landed on these shores. These few lines indicate that a one mile triangulation baseline was established near today’s Kurnell where the site of Cook’s landing is recorded.

 

Under Secretary for Lands, AR Jones in 1952 in the Goulburn Evening Post newspaper said in his Lake George History:…It was as early as September 1828, that Mitchell reported that three trigonometrical baselines had been laid down in the Colony; two in the vicinity of Botany Bay and one at the north end of Lake George, a mile in length. In respect of the Botany Bay baselines, Foster (1985), in his book Sir Thomas Livingston [sic] Mitchell and his World 1792-1855, stated:…In April 1828 Mitchell measured two bases, each of 832 yards on the sandy shore of Botany Bay. Brock (2006) stated something similar:…Mitchell measured two baselines in April 1828 as the foundation for his triangulation survey, each of 832 yards (760.781 metres) in length, along the sands of the shore at Botany Bay.

 

Even though Mitchell’s and the others’ dates did not align it seemed highly unlikely that Mitchell set down a baseline in January 1828 and then two baselines later in April 1828; all for the same purpose and all at Botany Bay. Also, why two baselines of equal length? There seemed to be no advantage of going to the extra effort of making their lengths equal when the amount of following survey work would be the same no matter what the length of the baselines. The length of 832 yards was also puzzling; why not 880 yards which was half a mile (1 mile is 1 760 yards).  A plausible explanation was sought and is detailed at Annexure D, A Plausible Reconciliation of Mitchell’s Botany Bay Baselines. From the Botany Bay baseline(s) (1), Mitchell used a basenet to create a more substantial baseline formed by the line between the Sydney Lighthouse and a small hill on the south side of the bay. The terminals of this baseline offered views to the peaks of Mount Jellore in the south west, various prominent peaks in the Blue Mountains to the north west, and Mount Warrawolong to the north.

 

Sometime in the period between February-April 1828, a baseline was measured, by Mitchell and Robert Dixon, at the north end of Lake George (2). Please refer to Figure 8 below. The baseline at Lake George was some 5 kilometres south of today’s town of Collector between today’s highway and the escarpment and was 1 mile in length. The measuring apparatus used was two tent poles of English Deal (Fir or Pine wood) about 2 inches in diameter; one 10 feet 2 inches and the other 9 feet 11 inches long.

 

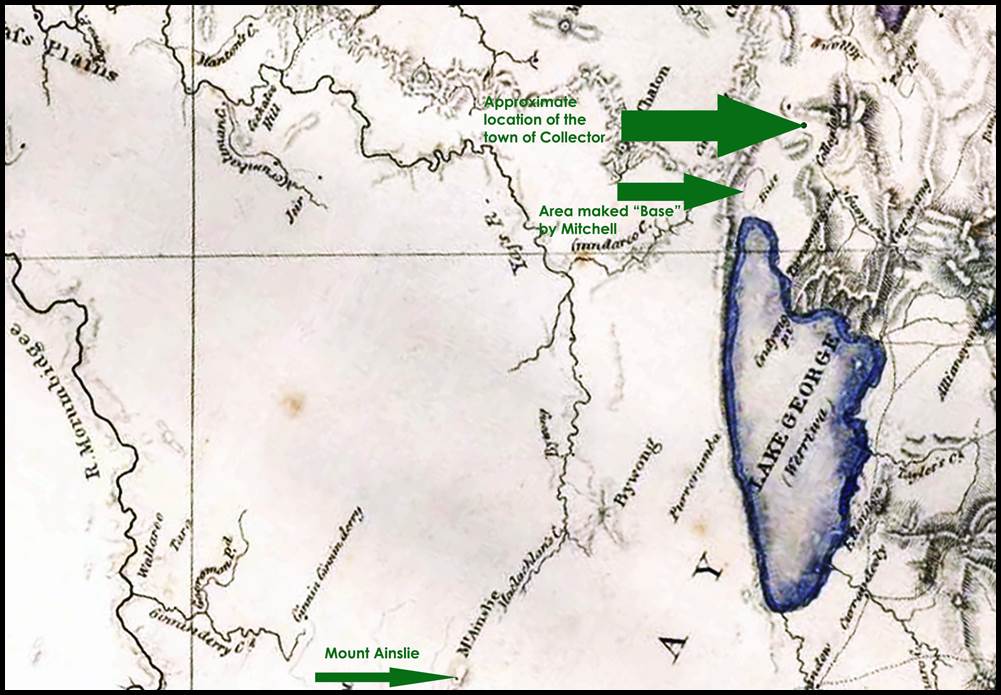
Figure 8 : Section of Mitchell’s 1834 map showing the area where he located his 1828 1 mile baseline

(courtesy Hunter Living Histories, University of Newcastle).

 

In late May 1828, while Mitchell was selecting triangulation stations, he stood on Mount Jellore outside of Mittagong. From Jellore he noted that in the clear Australian atmosphere visibility of between 90 and 110 miles was achievable as he could see Mount Warrawolong, Mount Hay in the Blue Mountains and the Sydney Lighthouse. The following year, when observing at Mount Warrawolong on 14 July 1829 he saw Jellore.

 

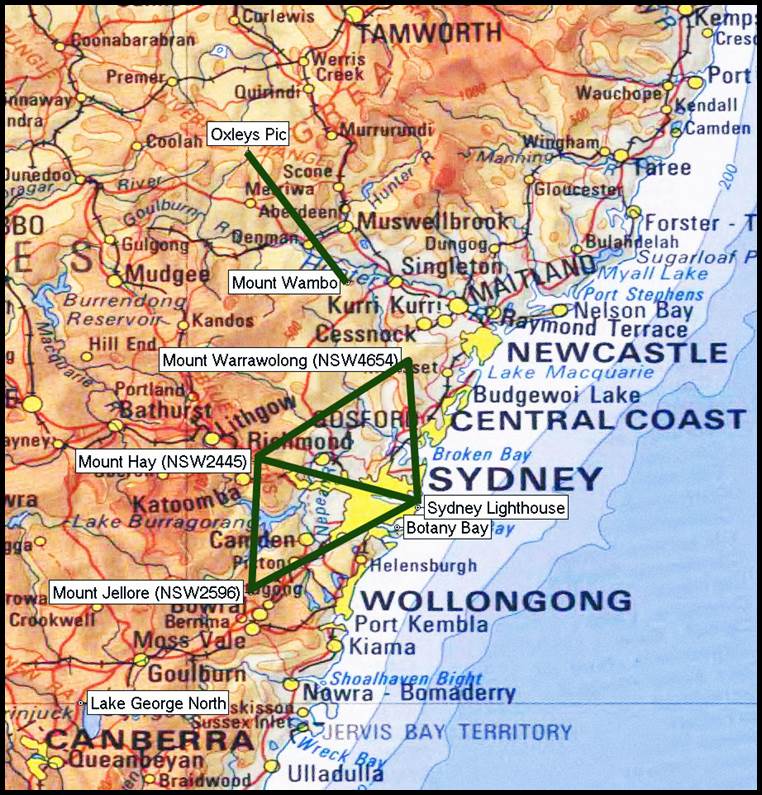
Figure 9 : Section of 1: 1 000 000 scale map showing (i) the locations of Sydney Lighthouse, Mount Jellore, to its south west outside of Mittagong; Mount Hay, to its north west, north of Katoomba; and Mount Warrawolong, to its north and south west of Newcastle, forming the primary 1828-29 triangles; (ii) the site of the Botany Bay and Lake George North baselines; (iii) the 60 mile check line Oxleys Pic to Mount Wambo.

 

The first series of Mitchell’s triangles extended from the baseline at Lake George to Sydney Lighthouse, and was the result of observations made in June, July, and August, of 1828. Notably this triangulation extended to Mount Hay and Mount Tomah, which are the highest points of the Blue Mountains (note that the Blue Mountains’ peaks of Mount Hay, Mount Banks (previously King Georges Mount), and Mount Tomah, all mentioned in the literature are relatively close to one another so appear to have become confused in some reports).

 

Triangulation operations were continued across the northern portion of the colony in June, 1829. Ultimately Mount Jellore, Mount Hay and Mount Warrawolong became the principal points on the triangulation, since from them may be seen the summits of all the higher ranges of the present Colony. Please refer to Figure 9 above. The triangulation was connected to the observatory at Parramatta by a traverse with a Gunter’s chain. Stations in the triangulation could now be located by their geographical coordinates of latitude and longitude relative to that of the observatory.

 

At the northern extent of Mitchell’s triangulation, on the Liverpool Plains (3) in the region of today’s Quirindi, in 1831 Robert Dixon established a three mile base of verification. The measuring apparatus is not specified. Dixon’s work included a connection to the triangulation from the south. From this baseline and basenet observations, the distance between stations on Oxley's Pic (Pic being French for Peak; station today is named Wereid), south west of Quirindi, and Mount Wambo, outside of Singleton, was calculated. This same distance was also determined through the triangulation from the Lake George baseline. A comparison of the two distances showed the difference to be a few yards. The triangulation was subsequently carried northward beyond the Liverpool Plains to the region of today’s New South Wales border with Queensland.

 

Mitchell however, did not only rely on baselines to check the triangulation. Stations in the triangulation had calculated geographical coordinates of latitude and longitude relative to that of the Parramatta observatory. On stations in the triangulation near the parallels of 30° and 35° south, and also close to having the same calculated longitude, Mitchell observed astronomical latitude. To remove any origin inconsistencies in the different determinations of latitude, Mitchell then took the difference between two stations calculated latitudes and the same two stations astronomically derived latitudes. Over a meridian arc of some 350 miles (550 kilometres) these two differences coinciding, without any sensible difference…have been considered as affording proofs of a sufficient degree of accuracy for the present purpose.

 

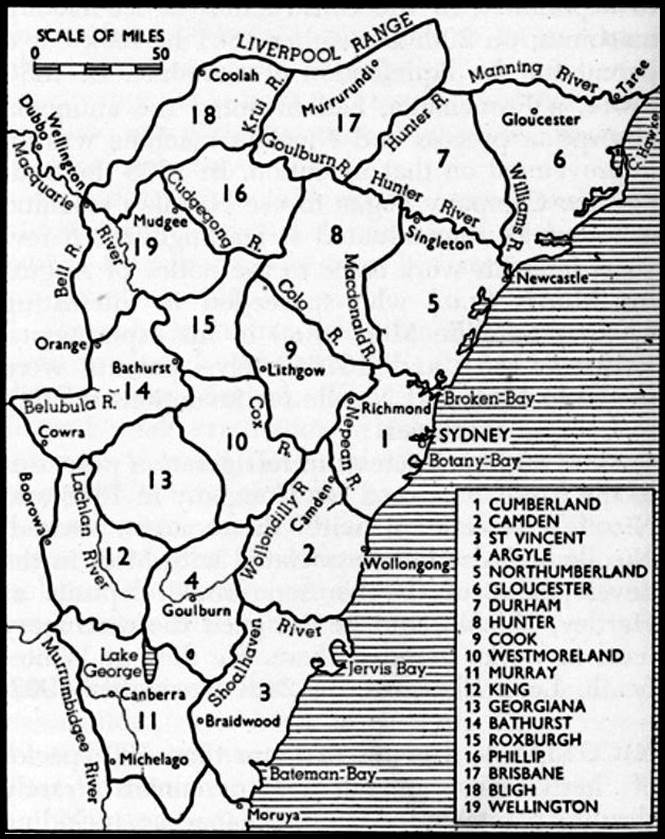
Figure 10 : Diagram showing The Nineteen Counties mapped from the control established by Mitchell’s triangulation.

 

By 1834, Mitchell had prepared a map, commonly called the Map of the Nineteen Counties, based on this triangulation covering the nineteen counties then existing around Sydney. Please refer to Figure 10 above.

 

Among Mitchell’s surveyors were Robert Dixon and Robert Hoddle. In addition to Dixon’s work already described above, Dixon also established a baseline in 1839 south of Ipswich (4). At this time what was to become Queensland was still New South Wales, and the Moreton Bay region was seen as suitable for settlement. Later in 1849 James Charles Burnett (1815-1854) measured an approximately north-south baseline south of Jondaryan, please refer to Figure 31 further on. The later Jondaryan baseline was established in this same area except it ran approximately east-west. The Ipswich and Jondaryan baselines are discussed in more detail in the later section on Queensland. Robert Hoddle later became associated with surveys of early Melbourne and is further discussed in the Victorian section below. The locations of the baselines established during Mitchell’s administration may be viewed via this link.

 

The need to establish the colonial boundary between South Australia and New South Wales saw Charles James Tyers under the direction of Surveyor General Mitchell sail to Melbourne from Sydney in 1839 (at that time what was to become Victoria was known as the Port Phillip District of New South Wales and Melbourne was yet to be formally named). From Melbourne, Tyers observed a triangulation west to enable the South Australia-New South Wales border meridian at longitude 141° east, to be marked on the ground. A few years earlier in 1836, Robert Russell, the senior of a three man party, was sent from Sydney to Melbourne with specific survey instructions. Part of this party’s initial work was a small triangulation survey. The work of Tyers and Russell is discussed in more detail in the later section on Victoria.

 

The manuscript Trigonometrical Survey of Port Jackson : commenced as a military survey by order of General Darling and continued as civil duties permitted or required, by Lieutenant Colonel Sir TL Mitchell, Surveyor General of New South Wales, was published in 1853, and contained the first accurate maps of the area. Around that time Mitchell had written to Frederick Peel, Under Secretary for the Colonies, that in 1829, by instruction of Governor Darling he had commenced a military survey of Sydney Harbour 'a work which, amidst many civil duties I could only perform at intervals of leisure’.

 

This 1853 manuscript also contained two panoramic sketches based on angular observations taken at two points “A” and “B” which are shown in Figure 11 below. The angular observations at “A”, located south of Point Piper in today’s Bellevue Hill, were taken in 1829 based on the bearing to Sydney Light, set as 0 degrees; the angular observations at “B”, on Dobroyd Hill, in today’s Balgowlah Heights, were taken in 1853 based on the bearing to “A” set as 0 degrees. These views show that Sydney Light and North Head were visible from “A” as was Dawes Battery and the tower of Fort Macquarie in the region of the Botanic Gardens. There is no indication in this publication of any baselines despite it being recorded that in 1828 Thomas Florance (1783-1867) measured two baselines; one baseline located at North Head; the other in the vicinity of the Botanical Gardens. It is concluded that these two baselines were used only to control this local Port Jackson mapping survey.

 

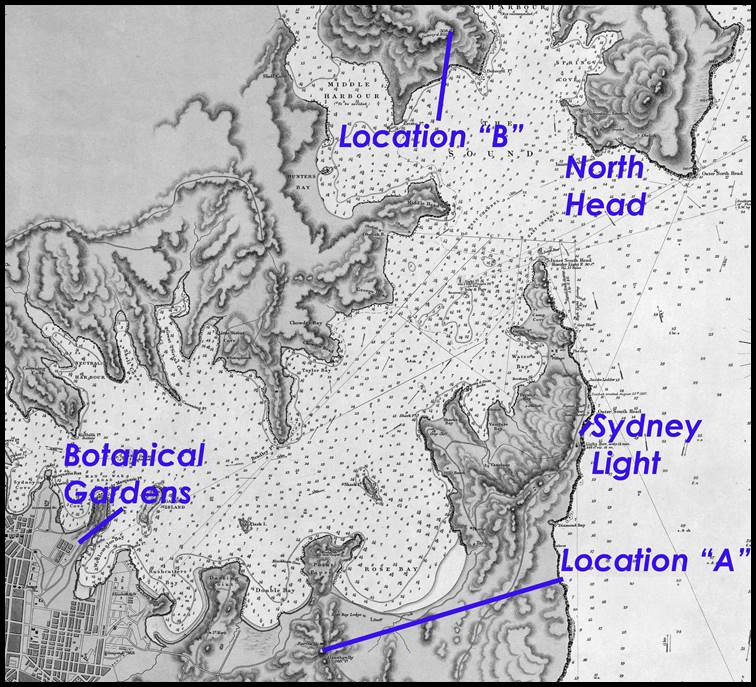
Figure 11 : Section of 1857 map of Port Jackson by British Admiralty, showing the relativity of locations reportedly used by Mitchell/Florance for his/their baselines and angular observations

(courtesy National Library Australia, nla.obj-233809197).

 

Requiring an accurate, detailed map of Sydney, the City Commissioners in 1854 authorised a triangulation survey of the city. This triangulation was controlled by a baseline at Waterloo Swamp (today encompassing the suburbs of Waterloo and Zetland), 5 miles from Sydney, and the second located at Paddington. The Waterloo Swamp baseline of 3 250 feet was measured eight or nine times with a 100 foot chain and afterwards with 20 foot rods, tested before and after each day's work. The Paddington baseline of 13 192 feet, was measured with rods provided with adjusting screws at the ends. Development has meant that any sign of these two baselines disappeared long ago.

 

Despite all Mitchell’s and his colleague’s work, and perhaps because it was undertaken with what equipment was available, which was not necessarily fit for purpose, and as his survey points and baselines were not permanently marked, New South Wales started its triangulation again in 1867.  

 

 

 

Triangulation Baselines pre 1912

 

New South Wales from 1867 to 1912

In 1865, George Robarts Smalley, Government Astronomer, had written to Colonial Secretary, (later Sir) Charles Cowper (1807–1875), regarding the Sydney Observatory of which he had charge. Please refer to Smalley’s letter at Annexure A. Smalley had previously communicated with the British Astronomer Royal, George Biddell Airy (1801-1892), who is best known for his establishment of Greenwich as the location of the prime meridian. Airy, who also established parameters for the figure of the earth in the northern hemisphere suggested to Smalley that:…the province of New South Wales, and the continent of Australia generally, may be the scene of important geodetic and hydrographic operations, either for the purpose of territorial survey of a high order, or for the scientific measures of arcs of meridian and arcs of parallel. Works of this class should originate from the Sydney Observatory as starting point.

 

Smalley therefore proposed that:…as there has never been any triangulation of this colony upon which sufficient reliance can be placed; and it is equally certain that such a work, properly carried out, is of the highest public importance. Smalley was thus given charge of commencing the triangulation of New South Wales, starting from a new baseline. In accordance with the instructions he received dated 16 January, 1867, Smalley then met with Surveyor General, Philip Francis Adams (1828–1901). Please refer to Annexure E. Later in July 1867, Adams and Smalley met District Surveyor Edward Twynam (1832-1923) at Lake George, and after a careful examination, unanimously agreed that no better site [for a triangulation baseline] could be conveniently selected.

 

By June 1869, Smalley reported that he had selected a line of about 5 miles 64 chains 72 links (30 672 feet or about 5.81 miles), the ends of which were on hills supposed to be not liable to inundation. A stone column had been completed at one end, and at the other end, construction of a column was in progress. Smalley passed away in September 1970. Adams then took charge of the work but found that the country had been recently devastated by the greatest flood then ever known. The waters of the lake had risen to nearly a metre over the baseline’s northern terminal, submerging about one and a half miles of the baseline. He thus altered the direction of the baseline so that the southern terminal was now further east. However, by May 1871, Adams had reported slow progress and thus by the end of 1872 it had been determined that another baseline should be begun.

 

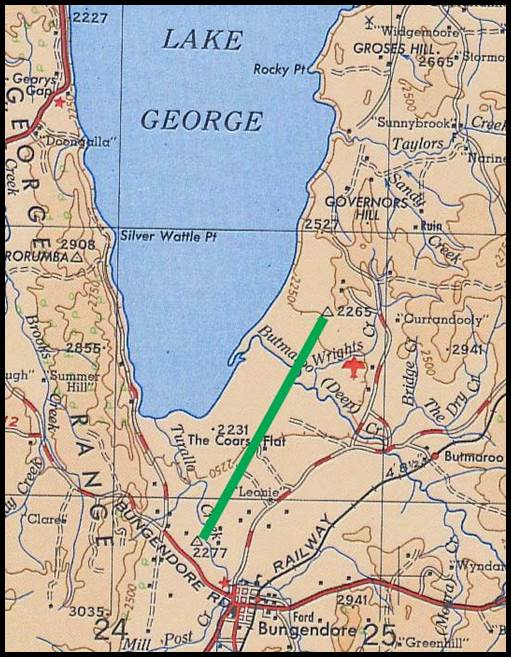
Figure 12 : Section of R502 1: 250 000 scale SI55-16 Canberra map sheet showing the location of the 1873 Lake George baseline in green.

The location of this baseline as depicted in the County of Murray, Parish of Currandooly map sheet may be viewed via this link.

 

The work of the third baseline was commenced on the 2 January, 1873, this line being about half a mile east of the second line, beginning at the lowest portion of the swamp, north of Deep Creek, which was then only eighteen inches above lake level. Please refer to Figure 12 above. Arthur Charles Betts (1843-c1890) and Leonard Abington Vessey (1847–1880) undertook measuring operations during 1873, completing their work by 31 January 1874. The Lake George (16) baseline’s length was reported to be 29 286 feet (about 5½ miles or 9 kilometres). Betts and Vessey used a set of three wooden measuring bars with a nominal length of 10 feet. Smalley had recovered the well-seasoned pine bars belonging to the Government of New South Wales, from the Lands Office in Melbourne where they had errantly been deposited.

 

Far from performing as first Denison in 1857, and later Smalley had forecast, the wooden bars reportedly acted in a most incomprehensible manner, and for some time defied all efforts to account for certain spasmodic contractions and expansions, which caused the loss of several days' work. It turned out however that the days upon which the insular action had been observed had been preceded by a low minimum temperature during the night, and if 60 degrees was reached or a lower temperature, the bars did not recover their normal length until many hour’s exposure to a temperature of 90 degrees or upwards. After this discovery the bars were carefully put to bed every night, blankets being thrown over them, and two small kerosene lamps left burning under them every night. The wooden measuring bars were also compared every day with the New South Wales 10 feet wrought iron standard OI4, mentioned above. Such was the care taken that the possible error was estimated at one inch and three-eighths for the 5½ miles (35 millimetres or less than 4 millimetres per kilometre). The difference between the lengths of the base as found from the measurement and remeasurement was 0.542 inches (14 millimetres or 1.5 millimetres per kilometre).

 

While Adams was instrumental in overseeing the completion of the Lake George baseline, he had earlier established another baseline. Adams baseline was established in 1859 near the Ellerslie Triangulation station some 20 kilometres north of Albury (10) with a length of 48 chains or a little over half a mile. The measuring apparatus was not unspecified. Please refer to Figure 13 below.

 

It was reported in 1880 that from Lake George triangles had been laid down for a considerable distance, extending as far as Albury. Presumably this triangulation closed on the Ellerslie baseline. If so, it was the last time this baseline was incorporated as later triangulation bypassed it.

 

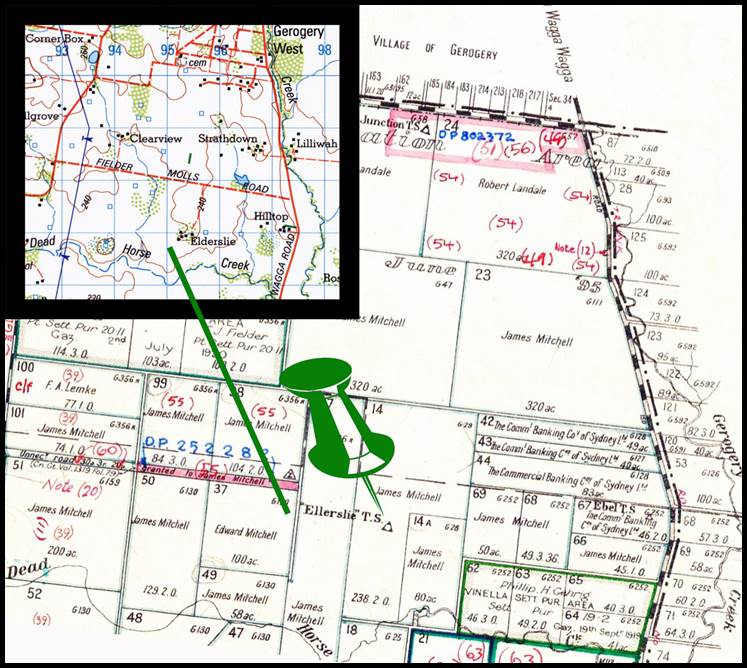
Figure 13 : The location of Ellerslie Triangulation station (green pin) as depicted in the County of Goulburn, Parish of Huon map; with insert of 8226 Walbundrie 1: 100 000 scale map showing Ellerslie Triangulation station would today be in close proximity to ELDERSLIE Homestead.

 

The New South Wales triangulation was also being extended west by John Sofala Chard (1853-1911). The Bullenbung baseline (17) was established by Chard with a steel band in 1875. The southern terminal was at Tollendool Hill; the northern terminal however was not identified by name. From the terminal coordinates the baseline was calculated to have been 11 454 metres (7.1 miles) long. Named after the Parish of Bullenbung, the baseline was located between Wagga Wagga and Lockhart some 40 kilometres west of Wagga Wagga. Please refer to Figure 14 below.

 

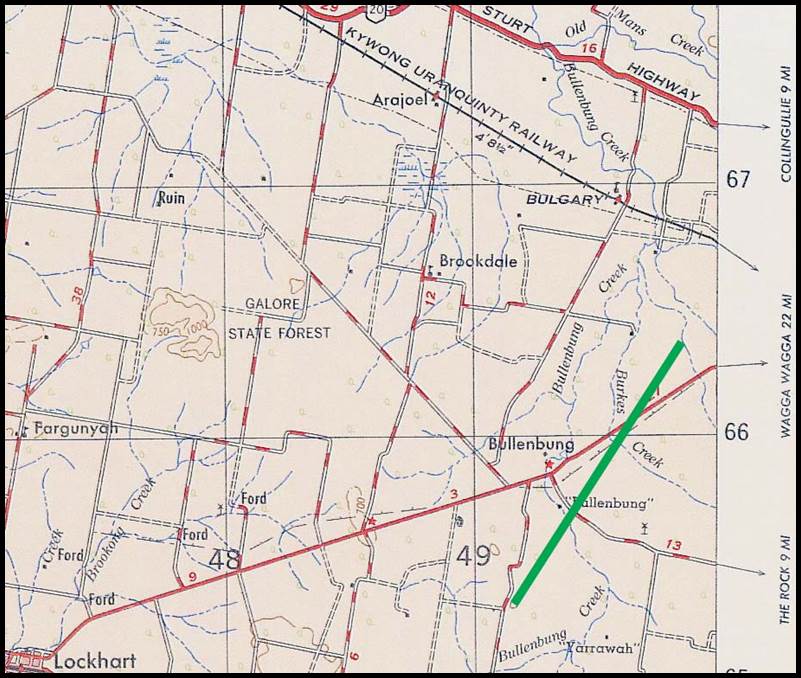
Figure 14 : Section of R502 1: 250 000 scale, SI55-14 Jerilderie map sheet showing the location of the Bullenbung baseline in green.

The location of this baseline as depicted in the section of the combined County of Mitchell, Parish of Bullenbung and County of Mitchell, Parish of Ashcroft map sheets, may be viewed via this link.

 

District Surveyor Edward Twynam (1832-1923, Surveyor General, or equivalent, New South Wales 1887-1901) reported to Surveyor General Philip Francis Adams on 30 September 1879, that he had completed his work measuring the Newcastle baseline (18).

 

In his handwritten report (Twynam, 1879), Twynam wrote:…In accordance with your instructions I have measured a baseline by means of steel riband within Australian Agricultural Company’s Estate of two thousand acres, to meet the requirements for the immediate trigonometrical survey of the environs of Newcastle, in anticipation of the general trigonometrical survey reaching that place…I found the baseline laid out by Mr Brownrigg under your direction and cleared of timber and other obstructions; the conditions of the ground are generally favourable, and the site of the base appears to be judiciously selected for securing well condition triangles…For convenient reference the base was divided by proper marks into four sections and the computation of measurement and remeasurement…from which it appears that the greatest difference in any section is 0.046 feet, whilst from the fact of the errors nearly balancing, the difference on the total measurement and remeasurement is very minute being 0.001 of a foot in a distance of upwards of 7 200 feet [some 1.4 miles]…The steel riband used comprises three lengths of 100 feet, 66 feet and 200 feet respectively…the steel ribands 100 feet and 66 feet have been tested at the Observatory…The length of the 200 feet riband was…adjusted to the length laid down on section 57-58 of the baseline; this length had originally been measured with the 100 feet riband.

 

The Australian Agricultural Company’s Estate of two thousand acres, was shown on the County Northumberland, Parish of Newcastle 1959 plan. The extent of the Australian Agricultural Company’s holdings was transferred to the 1892 Map of the country around Newcastle, New South Wales by Major Thomas Samuel Parrott, please refer to Figure 15 below. Today this area is covered by suburban Newcastle. The exact location of Twynam’s baseline within this area is unclear but at some point, it did cross the 1879 road to the racecourse which is possibly the road shown in the 1892 map. Presumably, like the Ellerslie baseline, the triangulation north from Sydney closed on the Newcastle baseline, and if so, it was the last time this baseline was incorporated as later triangulation bypassed it.

 

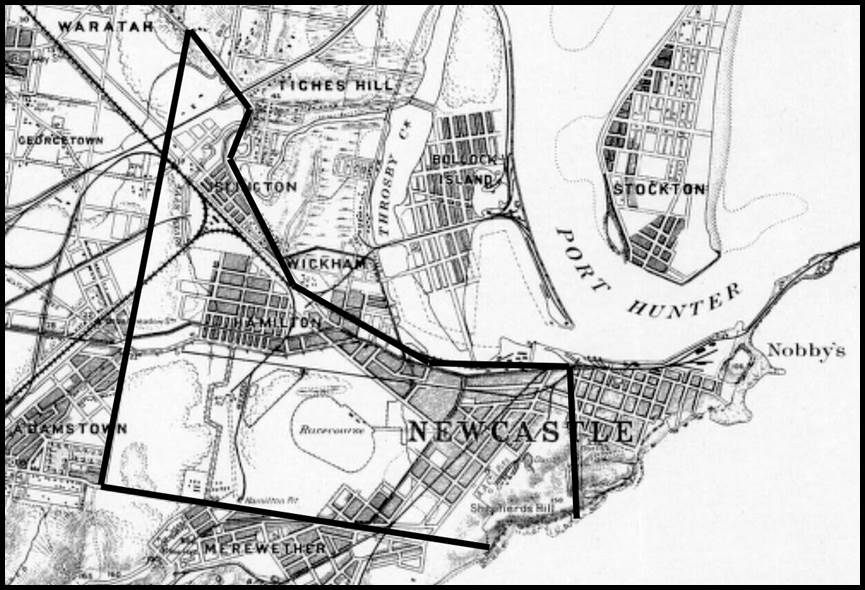
Figure 15 : The Australian Agricultural Company’s Estate of two thousand acres, indicated by the black boundary, on a section of the 1892 Map of the country around Newcastle New South Wales by Major Thomas Samuel Parrott

(courtesy National Library Australia, nla.obj-229953448).

 

The New South Wales triangulation was now being extended to Cooma in the south, Wagga Wagga in the south west; to the triangulation station Rocks, just west of Bathurst in the north west; and to Bowen Mountain to the north west of Richmond near the town of the same name. The terrain forced William Jacomb Conder’s (?-1890) triangulation network from Lake George to travel by Boorowa and Cowra to the vicinity of Bathurst where it could then turn east towards Richmond. The direct chain from Lake George to Richmond apparently gave some difficulty, with several stations abandoned, and was not completed until 1881. Conder established the 7 mile Richmond base of verification (19) in 1879-80, at Ham Common. Please refer to Figure 16 below.

 

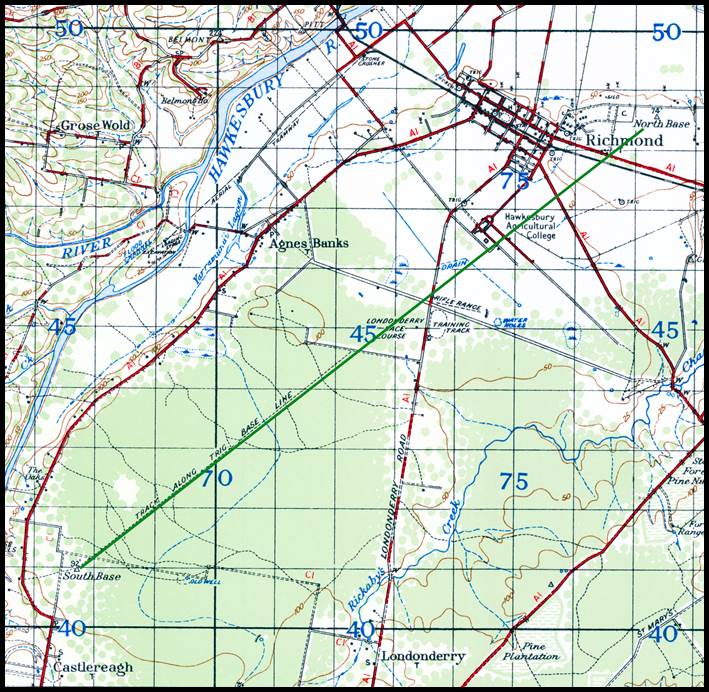
Figure 16 : Section of 1942 1: 63 360 No.416 Zone 8 Windsor map sheet showing the location of the Richmond baseline in green.

The location of this baseline as depicted in the section of the combined County of Cumberland, Parish of Ham Common and County of Cumberland, Parish of Castlereagh map sheets may be viewed via this link.

 

An 1880 report on the Richmond baseline, stated that:…The distance was measured twice over, first from north to south with the wooden bars, then back again from south to north with simple steel bars which Mr Adams has had constructed for the purpose…The standard bar is kept in a vaulted cellar, constructed for the purpose, in which the temperature is as equable as can well be. Every night on finishing the day's work, and every morning before commencing, each bar - of which there were three, each ten feet in length - was carefully compared with the standard; an account of the temperature of the bars, ascertained by means of thermometers let into them, was also carefully kept at intervals during the day. The steel bars are also three in number, and each ten foot in length; each bar is padded with felt and enclosed in a wooden box, and the box itself is similarly padded and enclosed in an outer wooden box with square and true faces. About half an inch of each bar projects from the ends of the boxes, and on each of these ends there is embedded a small disc of silver, and the distance between the centres of the discs should be exactly ten feet, when the iron is at a certain specified degree of temperature. If the metal is above that degree of temperature, the bar will have expanded, and it will measure a trifle more than ten feet. On the other hand, should the temperature be below the specified point, the metal will contract, and the length of the bar will be under ten feet. It is necessary therefore that the temperature of the bar should be constantly watched, for, this being known, the length of the bar can be at once predicted. For this purpose there are thermometers attached to each bar, the bulbs of which are in close contact with the metal, and the temperature they indicate is constantly recorded…At the north end of the Richmond base, in consequence of doubtful foundation, the concrete foundation was placed some eight feet below the surface. At the south end the terminal dot is almost level with the surface…the amount of discrepancy between the measurement by means of wooden bars and the remeasurement by steel bars has not been completely investigated; but sufficient is known to show that the error cannot exceed two or three inches in seven miles, and will in all probability be reduced to within one inch.

 

An interesting aside is that in November 1879, Charles Todd, CMG (1826-1910), then Postmaster General and Government Astronomer, South Australia, attended a conference in Sydney. Whilst in Sydney Todd had the opportunity of visiting Richmond…, and examining the operations for the measuring of a baseline of verification in connection with the trigonometrical survey of the colony [of New South Wales].

 

For his measurement of the Richmond baseline, Conder used the same wooden bars that had been used for the Lake George baseline measurement. The difference between the two determinations of length, by wooden and steel bars respectively, was 0.662 of an inch in the total length of 7 miles (17 millimetres or 1.5 millimetres per kilometre). When the triangulation connected the Lake George baseline with the Richmond baseline, it was found that there was a discrepancy of only one and two thirds inches against the length of the Lake George baseline (42 millimetres or 5 millimetres per kilometre).

 

The Richmond baseline was remeasured with Invar band(s) in 1927 showing a difference of 0.2709 feet (about 85 millimetres or better than 10 millimetres per kilometre) between the 1927 and 1880 measurements.

 

The New South Wales triangulation now headed towards Bourke where a baseline was proposed to the south of the town along the railway. The marking of the base termini was completed in September 1915 and although the Bourke baseline had been selected, marked and connected to the network by October 1916 no measurement had been made and it was decided to partially suspend field operations due to war.

 

Chard’s Bullenbung baseline near Wagga Wagga was reported to have been abandoned. Nevertheless, the Bullenbung baseline was shown as part of the New South Wales triangulation in 1912, along with the Lake George, Richmond and Bourke baselines. Twynam’s Newcastle and Adam’s Ellerslie (Albury) baselines, however, are not shown on this plan of triangulation.

 

 

Triangulation Baselines pre 1912

 

South Australia

South Australia became a separate colony in 1834 with Colonel William Light (1786-1839), the first Surveyor General of South Australia (1836-1838), appointed in 1836. By mid 1837, Light had selected the site for the city of Adelaide and completed a triangulation survey of eight stations across some 75 square miles. The first baseline for the triangulation of South Australia was established in 1840 by Captain Edward Charles Frome (1802–1890). Over the next three years Frome observed a network of triangles extending over the hilly country to the east, south, and mid north of Adelaide. His triangulation stretched from the Fleurieu Peninsula in the south to around Orroroo in the north.

 

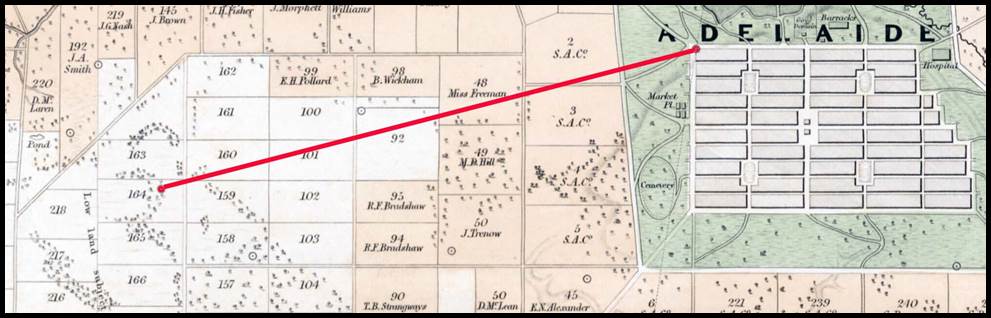
Figure 17 : Section of map (nla.obj-231421482), The District of Adelaide, South Australia; as divided into country sections, from the trigonometrical surveys of Colonel Light, late Surveyor General, showing the triangulation stations at the north west corner of the city and Masters Hill in Section No. 164, with the red line indicating Frome’s 1840 baseline.

 

South Australian surveyor Charles Hope Harris (1846-1915), under the auspices of then Surveyor General George Woodroffe Goyder (1826-1898) produced the South Australian Field Service Handbook for Government Surveyors, (Harris, 1880 & 1887). In this publication, Harris stated…A baseline of about three and a quarter miles was measured, near Adelaide, during the year 1840…it was measured six times, the greatest difference being +0.83 feet, and it extended from the north-west corner of the city to Masters' Hill, on Section No. 164, the mean length being stated at 17,462^.2 feet….A heavy steel chain, 100 feet in length, and a lighter chain 66 feet long were used to acquire the six measurements. A brass yard standard was used for reference.

 

The map, The District of Adelaide, South Australia; as divided into country sections, from the trigonometrical surveys of Colonel Light, late Surveyor General, showed not only the county sections but also the locations of the triangulation stations in and around Adelaide. Please refer to Figure 17 above for the relevant section of that map. A triangulation station was identified at the north west corner of the city and one in Section No. 164, shown as red dots in Figure 17. These locations transferred to a modern map as accurately as possible produced an equivalent distance, confirming that this was the most probable location of Frome’s Adelaide city 1840 baseline (6).

 

Figure 18 : Plaque indicating the location of Colonel Light’s Trig Station A, from where he commenced his survey for the city of Adelaide; the plaque is located on the corner of North and West Terrace; XNATMAP image.

 

During this investigation it was found that the triangulation station at the north west corner of the city was at the intersection of North and West Terrace and thus was undoubtedly Colonel Light’s Trig Station A, as shown in Figure 18 above. The original Masters Hill triangulation station in Section No. 164, is today located in the grounds of Adelaide Airport and appears to have been where the hangar for REX Regional Express now stands.

 

Harris continued…In course of extending the triangulation from time to time several other lines have been laid down, both for checks and as independent bases of operations for mapping localities, several hundred miles apart. No special value attaches to any them of but it may be of interest to indicate their positions, which are as follows :

 

Reported as No.2, Base of Verification, the circa 1850 Burra baseline (7) was listed to be between Bald Hill and Mount Bryan (also Mount Bryant) north of Burra near the town of Mount Bryan. The surveyor, apparatus used and actual length of the baseline was unrecorded. It is most likely however that the baseline was measured using 66 feet/100 link chain (this was the standard measuring apparatus of South Australian Government surveyors as described in Harris (1880)).  The distance between the peaks of Bald Hill and Mount Bryan was calculated to be nearly 17 miles (27 kilometres).

 

Reported as No.3 base, James Brooks chained a baseline from Hurd Hill (14), south westerly for 8 miles 336 links (42 461.76 feet or some 13 kilometres) in 1861 (the use of the word chain indicated that he probably used a 66 feet/100 link chain as given by Harris (1880)). Hurd Hill is some 20 kilometres almost due east of the town of Olary on the Barrier Highway in South Australia. Olary is about 120 kilometres south west of Broken Hill, NSW. Brooks’ triangulation extended from Black Rock to the eastern boundary of the then province.

 

Reported as No.4 base, Samuel Parry measured a baseline of 23 189.70 feet (4.4 miles or 7 kilometres), near Hookina (9) between two small hills called Castor and Pollux, from which the distances in the surrounding country were calculated. The area of the 1858 triangulation carried out by Parry was 8 000 square miles. Again, it was likely that this baseline was measured using the standard measuring apparatus of South Australian Government surveyors, a 66 feet/100 link chain.

 

Reported as No.5 base, John Moyle Painter (c1817-1863) commenced his survey by measuring a baseline at Mount Serle (8) in 1857, again most likely using the standard measuring apparatus of South Australian Government surveyors, a 66 feet/100 link chain. Mount Serle is some 50 kilometres east of Leigh Creek. From his baseline Painter worked northward to Mount Distance and Mount Hopeless towards the head of Lake Frome. George Woodroffe Goyder, then Assistant Surveyor General, reported on 9 July 1857, that due to the adverse character of the country in the region of Mount Serle the measured baseline was limited to two miles. This line extended southwards between Mounts Serle and McKinlay, on a bearing of 7° 29' 25" west of the true meridian. The baseline was measured by Painter and Lee (his assistant) with Goyder’s oversight, three times with…the three measurements varying but three quarters of an inch in the entire length, and the mean measurement adopted as the correct distance. The baseline was subsequently extended by a basenet, to Arcoona Bluff to the north, and Mount Rowe to the south, giving a total length of baseline of 7.55 miles (12 kilometres).

 

Reported as No.6 base, George Woodroffe Goyder (1826-1898) measured a baseline with an ordinary chain (again likely a 66 feet/100 link chain), at Termination Hill (11) some 50 kilometres north west of Leigh Creek in 1859. It was reported that this baseline ran 20 miles (105 861.90 feet or some 32 kilometres) true north of Termination Hill to the highest point of the Alromba Range, which intersected the line. This high point in the range was named Twentymile Hill.

 

Not included in the above list but of the same era was another baseline established by Goyder in 1859. The 58 423.20 feet (11 miles or 18 kilometres) baseline was again measured with an ordinary chain (66 feet/100 link chain), and was near Mount Margaret (12) some 150 kilometres north east of Coober Pedy.

 

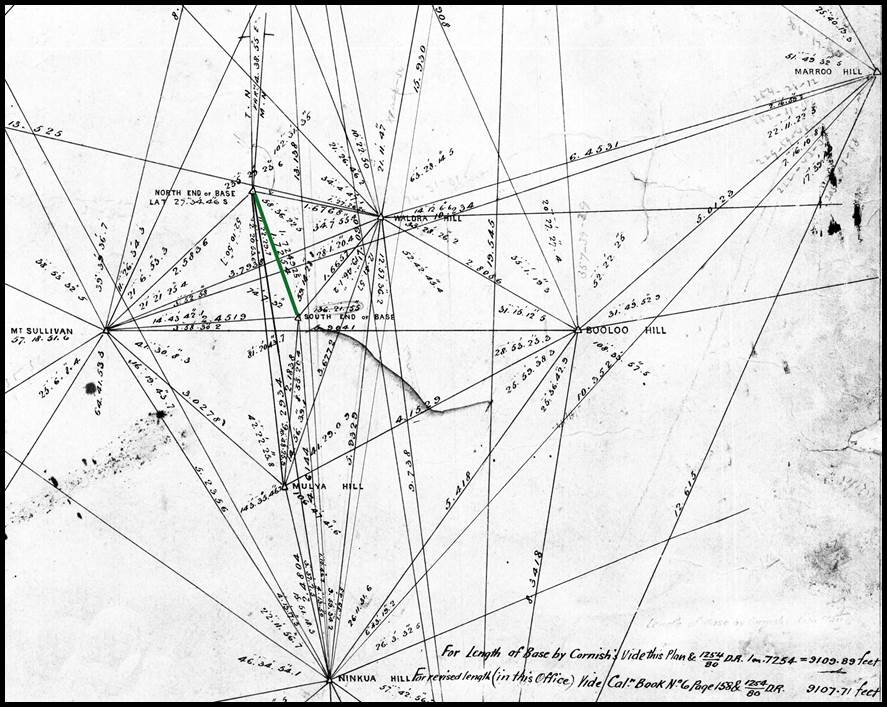
Figure 19 : Section of Cornish’s plan of triangulation in the region of his baseline at Thalepittinna Claypan (green line); in the bottom right corner it is noted that the baseline’s length was 9 107.71 feet.

 

The last pre 1912 triangulation baseline in South Australia appears to be that of Geodetic Surveyor William Henry Cornish (1850-1888) in 1880. Cornish measured his baseline situated in latitude 27° 35', longitude 138° 22' (today Thalepittinna Claypan) (20) eight times with Deal bars, 10 links in length, and twice with a steel bar also 10 links in length. All bars were standardised to the brass yard standard mentioned above. Two sets of measurements were made in summer and two in winter, corrections for temperature being carefully applied. The wooden bars instability finally led to the length of the baseline, as given by the steel rod alone, of 9 107.71 feet (1.7 miles or about 3 kilometres) being adopted (please refer to the annotation on the plan showing Cornish’s basenet at Figure 19 above. This length was considered to be correct to about 2 inches in a mile (around 30 millimetres per kilometre).

 

Thalepittinna Claypan is located to the west of Lake Howitt on the Birdsville Track about 250 kilometres north of Marree. Cornish’s triangulation extended from north of Hergott Springs, today Marree, to the northern boundary of South Australia, and eastward to the eastern boundary of the then province, encompassing Cooper Creek country from Innamincka to Lake Eyre. This base was used for the calculation of triangles extending about 150 miles east to the border with Queensland and 590 miles west as far as the boundary with Western Australia.

 

Using these existing baselines, as shown in Figure 20, South Australia continued its triangulation surveys to the north west and west of Adelaide. In May 1892 South Australia reportedly ceased such surveys.

 

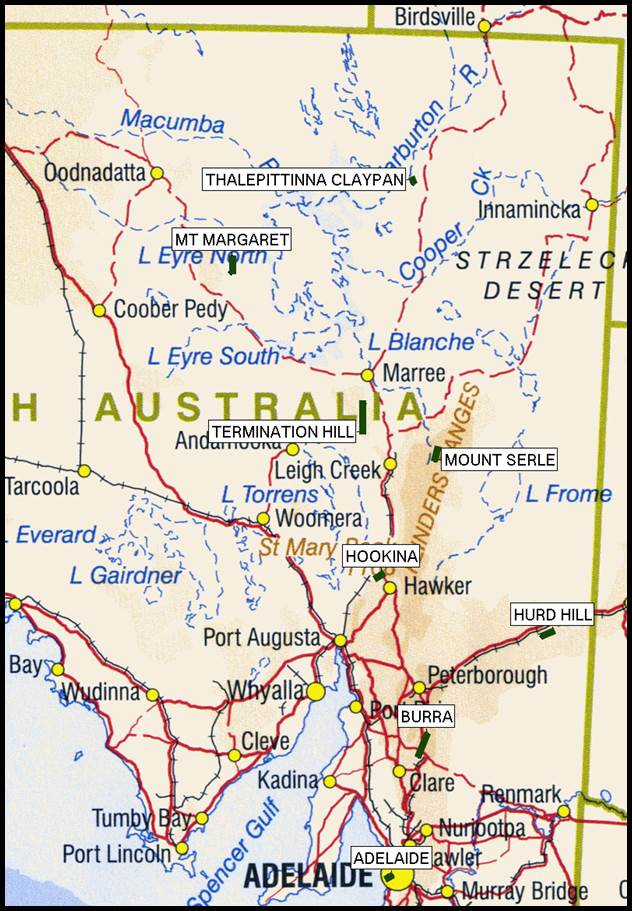
Figure 20 : Map showing the locations and length of the South Australian baselines to scale in green.

 

 

Triangulation Baselines pre 1912

 

Victoria

Victoria separated from New South Wales in 1851. Prior to separation, however, the need to establish the colonial boundary between South Australia and New South Wales saw Charles James Tyers (1806-1870) under the direction of Surveyor General of New South Wales, Thomas Mitchell sail to Melbourne from Sydney in 1839. From Melbourne, Tyers observed a triangulation consisting of fourteen stations and two astrono­mically determined bases being, Mount Eckersley, north of Portland, to Mount Sturgeon, near Hamilton, of 49.628 miles, and Cape Sir William Grant, on the coast at Portland, to Mount Eckersley, of 21.652 miles. Please refer to Figure 21 below. Suffice it to say that the result was that…this work forms no part of what is regarded as the trigonometrical survey proper of Victoria.

 

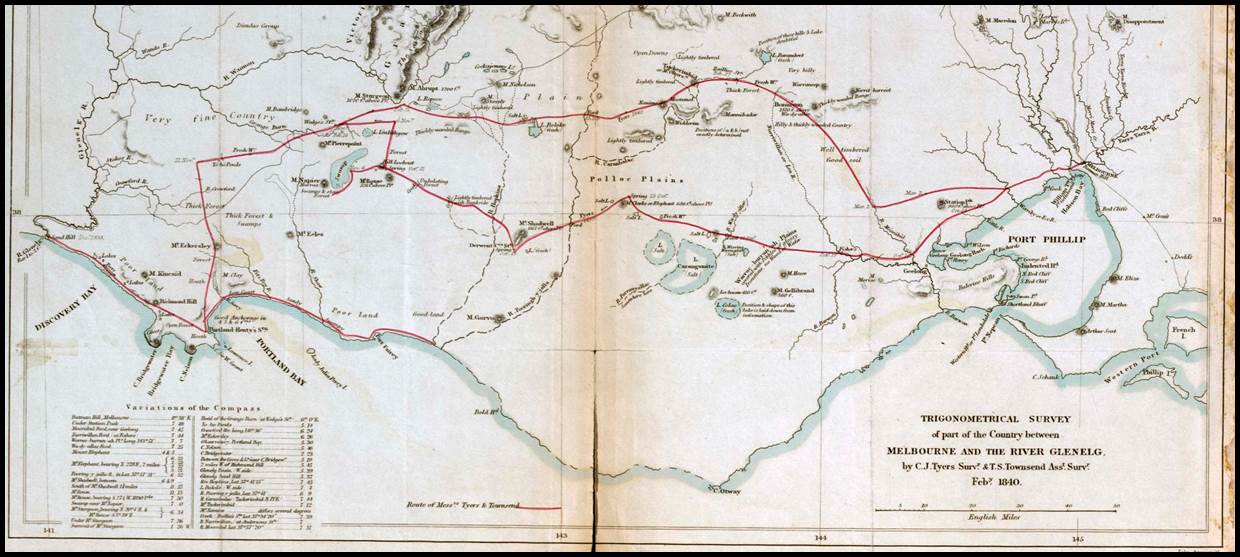
Figure 21 : March 1841 map of Trigonometrical survey of part of the country between Melbourne and The River Glenelg by CJ Tyers Surveyor & TS Townsend Assistant Surveyor

(courtesy National Library Australia nla.obj-232547618).

 

A few years earlier in 1836, Robert Russell (1808-1900), the senior of a three man party, was sent from Sydney to the Port Phillip Settlement, later to be named Melbourne, with specific survey instructions. Six months later in early 1837, New South Wales Governor Sir Richard Bourke (1777-1855), who had sent Russell and his men, along with Surveyor Robert Hoddle (1794-1881) arrived to inspect the Port Phillip Settlement. They found that Robert Russell had made a small triangulation survey, by means of which he had been able to prepare a plan showing illegal occupations. Bourke was dissatisfied with Russell’s progress and appointed Hoddle Surveyor-in-Charge of the Port Phillip District of New South Wales. Disgusted with Hoddle’s appointment, soon thereafter, Russell resigned his position in the Colonial Service. Hoddle is then credited with the design and layout of Melbourne city. Russell was later to recollect that to maintain the quality on his survey that a standard was brought down from Sydney (he thought it was a brass rod about eight feet long), and there were pegs left in the survey yard to check and maintain the chain to its correct length.

 

Now a colony in its own right, in October 1852, by direction of Victorian Governor Charles Joseph La Trobe (1801-1875), Clement Hodgkinson (1818-1893) commenced what is recorded as a detailed survey of Melbourne on trigonometrical principles between points on Batman's Hill, Point Ormond, at the mouth of the Yarra, on the high ground in Royal Park, and in Studley Park. No record of Hodgkinson’s baseline or subsequent triangulation has ever been found but it was believed to be of a high standard. The baseline on the Melbourne swamp (now occupied by the facilities associated with the Swanston and Appleton docks) was measured by Hodgkinson using tested pine rods properly compared with a standard yard measure belonging to the Customs Department.

 

What was initially to be a limited triangulation but ended up covering some 400 square miles, was commenced early in 1854 by George Christian Darbyshire (1820-1898). The constrained extent of the project meant that the triangulation baseline was not measured with appropriate care other than that the hundred link (66 feet) surveying chains used were adjusted with reference to the standard laid down at the Melbourne Government Offices. This standard however, may not have been derived from a strictly accurate source. Nevertheless, it was regarded as sufficiently precise for a triangulation of the initially small area. Over the extensive area finally surveyed the error was magnified and the final survey results were thus rendered mostly worthless.

 

Part of the Wimmera triangulation was also shown to be of suspect quality. It was found that the work of Surveyor Thomas Burr (1813–1866) was reported to have so many discrepancies that it appeared that Burr had read only two angles in each triangle, and found the third by taking their sum from 180 degrees…it was evident that in his triangulation Thomas Burr had no regard for the figure of the earth (if the triangles are sufficiently large then their three internal angles may sum to more than 180 degrees).

 

The actual Geodetic Survey of Victoria, by triangulation, was commenced in 1860, but in its earlier stages consisted more of the definition of meridian and parallel (chordal) lines embracing squares of one tenth of a degree than of triangulation. As will be seen this approach was still controlled by a baseline but the triangulation was undertaken along specific corridors.

 

Mid September 1858, saw the determination by triangulation of the difference of longitude between the Williamstown Observatory and a point selected in the Royal Park, to the north west of the Melbourne CBD, as the starting point of the first chief meridian. This chief meridian was at longitude 145 degrees east and was selected as it was then within two miles of the Williamstown Observatory. The Supplement to the Victoria Government Gazette of Friday, March 1, 1861 (Government of Victoria, 1861), published the position of (Williamstown Timeball) tower as 37° 52' 08" S, 144° 58' 30" E (9h 39m 54s) meaning the meridian at 145° east would be 1.5 minutes of arc further east or less than 2 miles in distance. Please refer to Figure 22 below. The chief meridian at 145° east was described as running from the waters of the Bay (near the Port Melbourne Railway Station, now a light rail stop) to the River Murray.

 

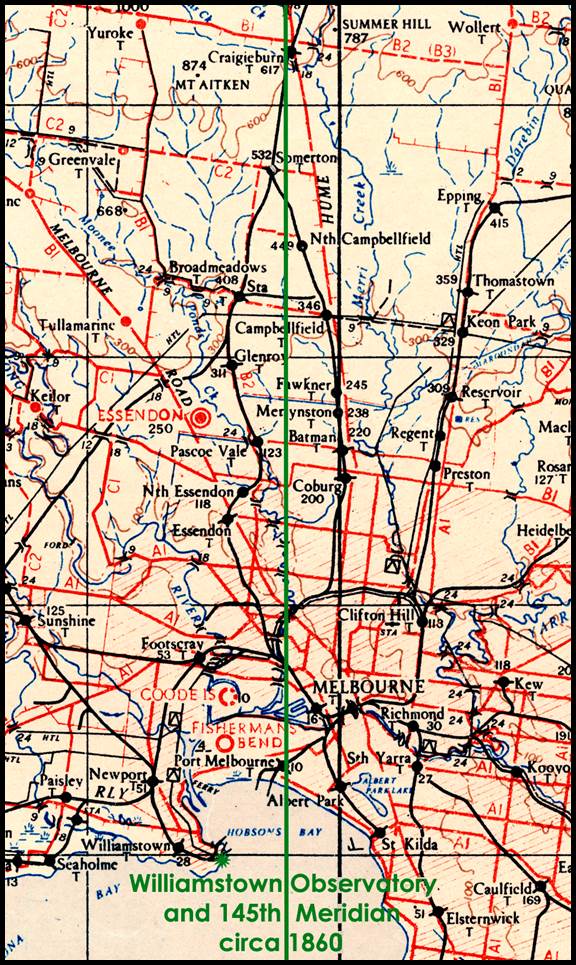
Figure 22 : Section of 1943 1: 253 440 scale SJ55-05 Melbourne map sheet showing the relative positions of the Williamstown observatory and the then 145 degree Meridian.

 

(It needs to be remembered that today the longitudes in Victoria are some 7 kilometres different from those used in the 1850s. Initially observatories determined longitude from their own astronomical observations completely independent of other observatories. The first determination of the difference in longitude between the Observatories of Sydney and Williamstown by the telegraphic exchange of clock signals, took place in 1861. Relative to Sydney, Williamstown was then at 144º 57’ 59” E (9h 39m 51.94s) longitude. The longitude of the Williamstown Observatory was, however, determined by observations of moon culminations in the years 1860, 1861, and 1862, resulting in the adopted value being 144º 54’ 42” E (9h 39m 38.8s) longitude, as it was found that Sydney Observatory had its own longitudinal error.)

 

Accurate triangulation enabled the difference in longitude between the Williamstown and Melbourne Observatories to be computed as +4 minutes of arc (16s). When this difference was applied to the longitude of Williamstown it gave the longitude of the Melbourne Observatory as 144º 58’ 42” E (9h 39m 54.8s) which was adopted until 1883. In the 1930s when the triangulation between the Sydney and Melbourne Observatories was complete and a common datum adopted, the old Williamstown Observatory coordinates were more accurate than those of Melbourne. It was apparent that, despite best efforts at the time, the Williamstown-Melbourne triangulation had introduced an error of around 15 seconds of arc (1s of time) resulting in the longitude value for the Melbourne Observatory being in error by that amount. A 1968 map last quoted the coordinates of the Melbourne Observatory as 37° 49' 52.47" S, 144° 58' 33.36" E, prior to all Australian geographical coordinates being standardised to AGD66).

 

The baseline for this initial triangulation from Williamstown to Royal Park was of two miles measured on the rails of the Williamstown and Melbourne Railway with a standard [100 link/66 feet] chain. The meridian was then traced, cleared, and measured with many observations of intermediate points that it was considered that in the forty miles the error of deviation from the true meridian did not exceed one inch. It was not until March, 1859, when the measurement of the first standard parallel (37° 48’ S latitude at that time) was commenced, starting from the first chief meridian near Flemington. Later, when the chief meridian had been extended as far as 37° S latitude (at that time near Puckapunyal) and subsequently to the Murray, that determinations had been made astronomically, and checked by careful triangulation, of the geographical position of Mounts Macedon and Warrenheip, also the intersection of the 37th parallel with the 144th meridian (near Maryborough) as well as the 145th. A most careful chain of triangulation was also carried along the parallels to fix the intersections of the secondary meridians.

 

It soon became evident that connecting distant localities with the chief meridian by running and measuring meridians through great expanses of country not required for survey was not cost-effective. Primary triangulation was the only way to rapidly reach the distant districts and connect the work generally. Robert Lewis John Ellery (1827-1908) Government Astronomer, who had been appointed to the position of Superintendent of the Geodetic Survey, in 1858, had been obliged to follow the meridian and parallel (chordal) line design for Victoria. When, in 1860, the work of defining meridian and parallel (chordal) lines was abandoned in favour of the traditional triangulation Ellery seized the opportunity to standardise the geodetic triangulation of Victoria.

 

Ellery measured a baseline on the Werribee Plains (13) some 30 kilometres south west of Melbourne between January and May 1860, using three iron bars each with a length of 10 feet (please refer to Figure 6 above). The southern end of the baseline was a point on the Melbourne to Geelong railway reserve, about 2 miles east of the Werribee railway station. The baseline extended 26 091.826 feet, or 4.941.16 miles to a point in direct line with Green Hill (today Eynesbury) on the western side of the Werribee River. Over 2 000 observations were made in the process of determining the length of the baseline. The measured base was subsequently extended by a basenet, a further 5.651 miles to Green Hill, its total length then being 55 931.65 feet or 10.593 miles. Please refer to Figures 23 and 24 below. The north and south ends of the measured baseline were permanently marked with sunken masonry piers, having in their upper surfaces a piece of brass carrying a platinum dot indicating the termini of the measure. These marks were then covered with heavy cap stones. Please refer to Figure 25 below. The mark at the end of the extension to the north, on Green Hill, consists of a sunken bluestone block with a projecting iron spike.

 

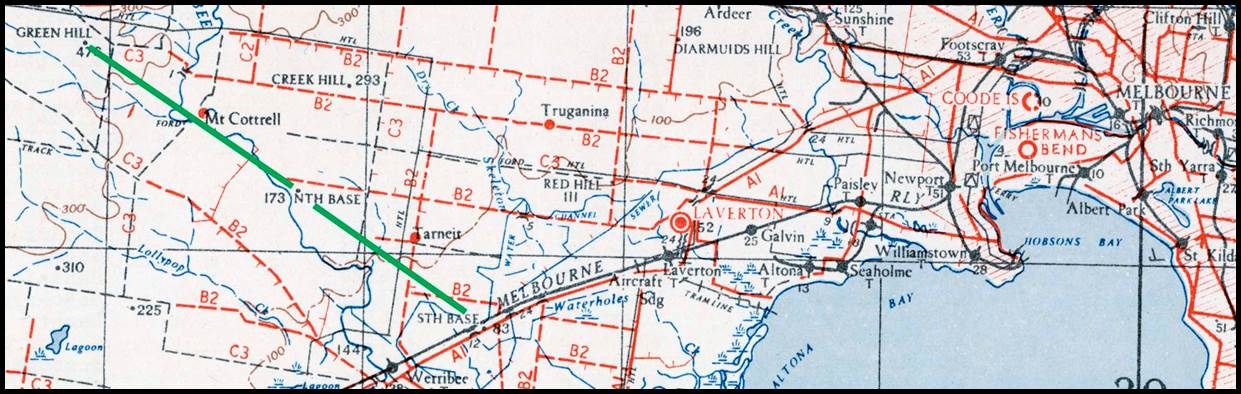
Figure 23 : Section of 1943 1: 253 440 scale SJ55-05 Melbourne map sheet showing the location of the Werribee baseline (green line); south base-north base-Green Hill.

 

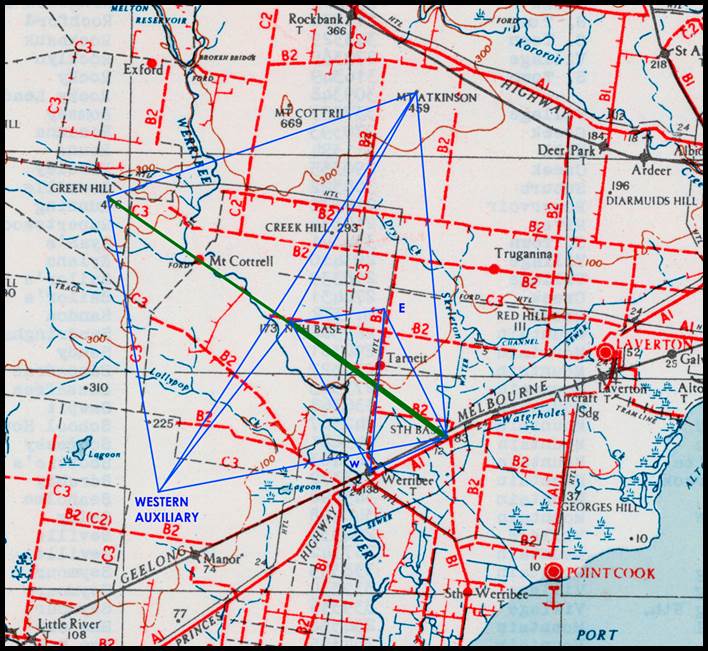
Figure 24 : Section of 1943 1: 253 440 scale SJ55-05 Melbourne map sheet showing the basenet configuration for the Werribee baseline (green line); south base-north base-Green Hill; points E, W, and Western Auxiliary are only located by scaling.

 

Figure 25 : Site of the South Base terminal at Werribee.

 

The three iron bars (identified as I, II and III) used by Ellery were constructed in Victoria. The bars were assumed to be 10 feet long but before being used for measurement were standardised against the 10 foot standard lent by the New South Wales Government, namely OI4, as described above. Victoria subsequently obtained its own standard from England being OI6, also described above. The three iron bars were fitted with steel ends, one flat and the other rounded to form a section of a sphere of 5 feet radius. They were used by being placed in series, with distances of about ¼ of an inch between the spherical end of one and the flat end of the next. The precise distance between these two terminals was then obtained by carefully inserting a graduated wedge between them until contact with each side was made. The graduations on the wedge then allowed the size of the gap to be read. The wedge was of hard bell metal, 7 inches long by 2 inches wide and the inclination of the faces was 30 minutes of arc. The iron bars were kept level during the measurement. A remeasurement of the southern 11 174.29 feet (2.11 miles) with the bars following the general inclination of the ground instead of being level as during the first measurement, was also undertaken. A difference of only 0.308 inches (about 8 millimetres), or about 0.15 inches per mile (better than 2 millimetres per kilometre) was recorded. This result indicated that the measurement of the Werribee baseline was the most accurate to date.

 

It would appear from Ellery’s own 1891 report that the measuring bars used at Werribee underwent a further calibration when Victoria received its own 10 feet (120 inch) standard OI6 in March 1862; their actual lengths in terms of the Melbourne edition of the British 10 feet standard were as follows :-

 

No. I : 119.99957 inches ;

No. II : 119.99318 inches ; and

No. III : 119.99997 inches, at a temperature of 62°F.

 

There is evidence that Ellery intended to remeasure the Werribee baseline with Colby type bars; a second measurement will shortly be commenced with some new rods, I have got made here - they are of Iron planed on the upper surface forming a compound bar…the iron and copper being permanently fixed together at one end, the other ends being free with marks for determining the expansion and interval between the rods. No physical verification of the rods or the remeasurement, however, have ever been found.

 

Immediately on completion of the baseline, triangulation was extended over the whole of Victoria with the exception of the north western mallee section. The north east region triangulation was by Alexander Black (1827-1897) and the south west work by Alexander Charles Allan (1831-1901). From 1862 to 1874, William Turton (1828-1906) undertook triangulation in the Gippsland area ranging from Bass Hill in the west through to Cape Howe and the New South Wales Border in the east. Before being sent to Gippsland, Turton had been involved in the latter stages of the measurement of the Werribee baseline during the first six months of 1860. Over the years Turton and Ellery both developed a profound respect for one another.

 

Figure 26 shows the locations of some of Turton’s stations including Baldhead, Baw Baw, Ben Cruachan, Boisdale, Elizabeth, Fatigue, Hoddinotts, Lakes Entrance, Merrimans, Seacombe, Shallow Inlet, Stockyard, Taylor, Toms Cap, Useful, Wellington and Woodside. At Seacombe, ti-tree was cleared in gaps about two to six hundred metres long and up to fifty metres wide; at Taylor, two thousand six hundred metres by fifty metres and at a station east of Lakes Entrance, three thousand two hundred metres by forty metres was cleared to established the necessary lines of sight to the other stations! The extent of this work prompted Turton to obtain Ellery’s approval for the equivalent of a reconnaissance party being formed, to carry out the clearing and station establishment independently of the main observation party. Considerable time could be saved by not having to return, sometimes on several separate occasions, to the same station to complete all the necessary work.

 

Figure 26 : Section of map showing the locations of Turton’s Gippsland triangulation stations.

 

On the extension of the primary triangulation westward to Mount Gambier and nearby Mount Schanck, in South Australia, Allan in July, 1864 reported that between these two mountains was an admirable site for a base of verification and that his proposed site was a much better one than that which had been selected for the Werribee Base. Allan recommended a length of 5.5 miles for the new baseline. While the intention to measure a baseline of verification was agreed, the actual work, however, was never performed.

 

During the twelve years of the Victorian survey, 209 primary stations were established and observed. The whole area of the colony of Victoria, with one exception, Ellery observed in 1873, had been triangulated with a primary triangulation almost equal in accuracy to any in the world, from a baseline, which was measured with all the refinement, skill and instrumental means then available. Ellery continued, pressing for two baselines of verification; one on the western boundary of Victoria, and one in Gippsland, to close and verify the triangulation. The end of the Victorian triangulation came without either baseline being established, which would have been a great disappointment to Ellery, for there was no independent check on the work of his department. The quality of the Victorian triangulation was only revealed in the 1930s.

 

The demarcation of the straight line, essentially from the source of the Murray River to Cape Howe, portion of the boundary between Victoria and New South Wales, in 1870 meant that the Victorian triangulation survey ranged north into southern New South Wales. Stations were established on Mount Pilot and Mount Kosciusko, and at Cape Howe. The line now known as the Black-Allan Line, after Alexander Black and Alexander Charles Allan assisted by Turton, previously mentioned, then being indicated by marks on the ground. When the New South Wales triangulation survey later reached that area the coordinates of Mount Pilot, Mount Tingaringy (today’s spelling), Mount Delegate (also Delegete) and Mount Buckle derived independently from both surveys could be compared. For the period, the overall quarter of a second of arc difference in latitude and around 8 seconds of arc difference in longitude were acceptable. The difference in longitude came from the fact that the longitude origin for the surveys came from independent observations at the Melbourne and Sydney observatories and until then the accuracy of one longitude determination against another had never occurred. This longitude difference was resolved in later years as technology developed.

 

Also associated with Ellery was a very small specific purpose triangulation in Melbourne in 1863. Some ten years earlier, at what was already a naval depot and signal station at Point Gellibrand, now Williamstown, a time ball was set up on the flagstaff there as a time signal facility for the port’s shipping; when the time ball dropped daily at usually 1PM the ship’s masters could adjust their clocks. Ellery was made Superintendent of the Observatory overseeing the time facility.

 

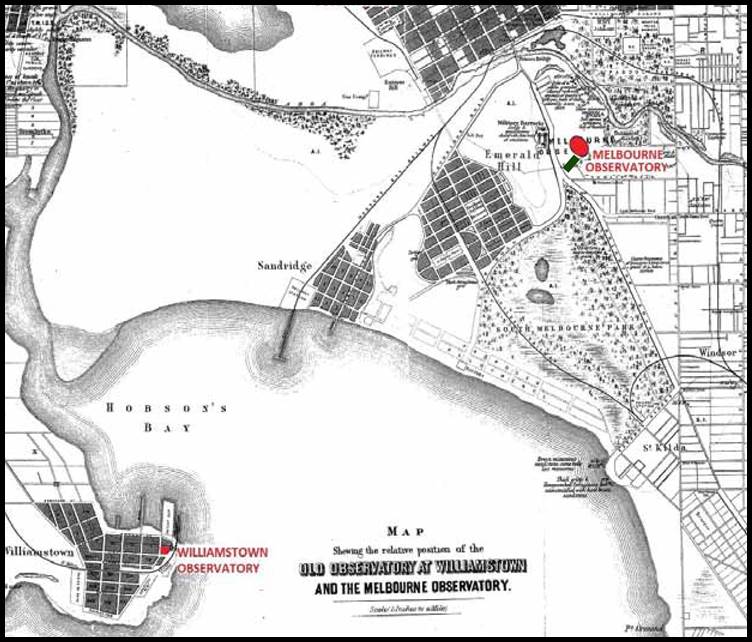
Figure 27 : Map showing the relative locations of the (old) Williamstown Observatory and (new) Melbourne Observatory and the location of the baseline near the Melbourne Observatory in green.

 

As the port developed it impacted the operation of the observatory equipment. The advent of the railway to Williamstown in 1859, such that trains were now travelling within 200 metres of the facility, dictated a new site be found. Due consideration of many factors saw the Melbourne Botanical Gardens selected as the site of the new facility. So as not to lose some ten years of observations establishing the longitude and hence time at Williamstown, a small triangulation was observed between the Williamstown and new Melbourne observatory. Please refer to Figure 27 above. The triangulation found that the difference in longitude between Williamstown and Melbourne was 4.0 minutes of arc. Thus, the longitude of the new Melbourne observatory was calculated to be 16.0 seconds of time greater than that of Williamstown.  

 

It is recorded that with the establishment of the Melbourne Observatory, Ellery used the Victorian standard OI6 to set out a baseline of 100 feet to enable the Surveyor’s 66 feet/100 link and Engineer’s 100 feet chains, to be accurately calibrated. The observations for this baseline were performed by Ellery in 1892-3. Terminal coordinates were also found for an Observatory baseline. This baseline was 750.3 feet (228.7 meters) long and ran approximately north-east to south-west to the west of the Observatory in the Botanic Gardens and outside the Observatory precinct. Please refer to Figure 28 below. It is uncertain if this baseline was part of the control for the Williamstown-Melbourne Observatory triangulation but the baseline was certainly not part of the survey control for the construction of the Shrine of Remembrance and was destroyed when the Shrine was built and landscaped.

 

Figure 28 : Map of the Melbourne Observatory environs in the late 1800s showing the relative locations of (A) the Melbourne Observatory baseline and (B) the Chain Standard baseline.

 

 

Triangulation Baselines pre 1912

 

Queensland

Before Queensland separated from New South Wales, in 1859, Robert Dixon (1800–1858) established a baseline in 1839. Dixon’s baseline, on what was known as the Normanby Plains, was in the region of today’s Harrisville, 20 kilometres south of Ipswich, near Warrill Creek. Please refer to Figures 29 and 30 below. The Ipswich baseline (4) of some 3 miles was measured with three Deal rods each ten feet long, tipped with brass. The survey from this base led to the first accurate map of the region. In May 1849, James Charles Burnett (1815-1854) measured a north-south baseline for his triangulation network. Burnett’s Jondaryan baseline (5) was 2 miles and 10 chains (170 chains) long and was situated about midway between Mount Maria and Mount Irving on the plain south of the town of Jondaryan on the Warrego Highway between Oakey and Dalby. Burnett used the same 3 Deal rods that Dixon had used in 1839. As is described below, Mount Maria and Mount Irving later became the terminals for the longer 7 mile, approximately east-west, Jondaryan baseline.  

 

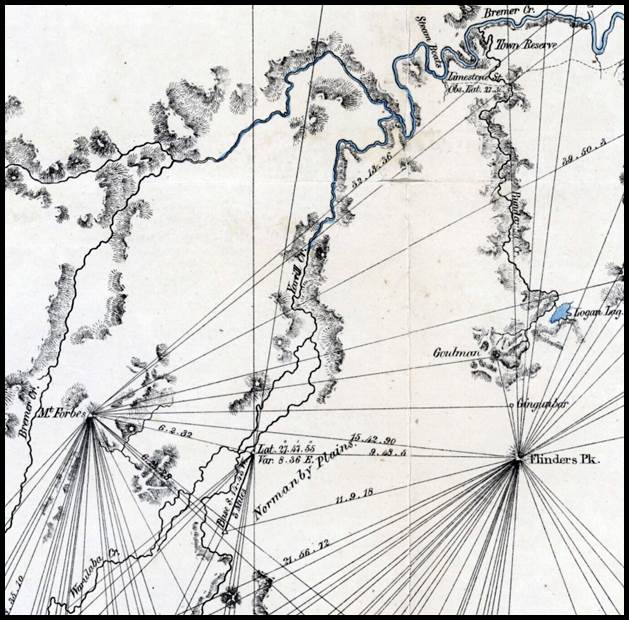
Figure 29 : Section of April 1840 map (nla.obj-2005473077), Trigonometrical Survey of the country at Moreton Bay, by Robert Dixon, showing the location of his baseline. Note that the peak shown as Mount Forbes by Dixon is today named Mount Walker with Mount Forbes a lesser peak to the north.

 

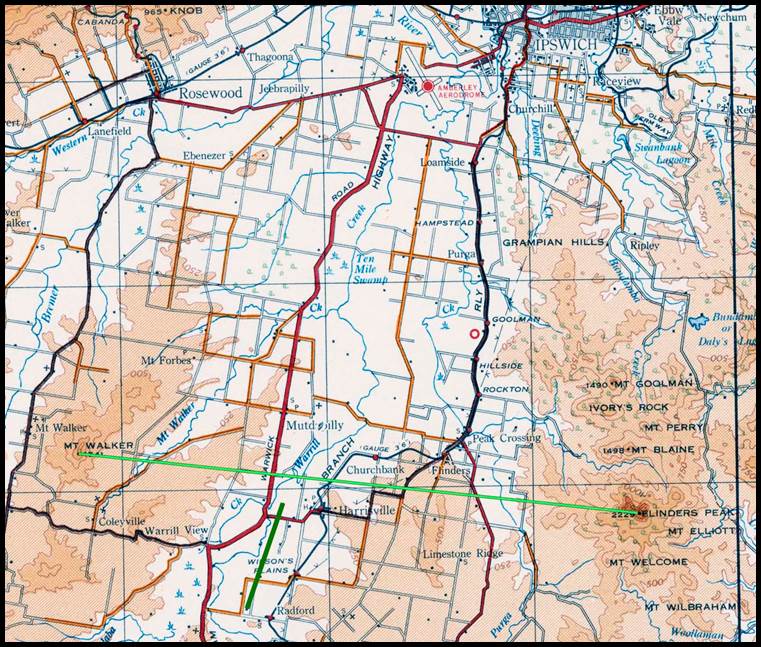
Figure 30 : Section of 1955 1: 253 440 scale SG56-14 Ipswich map sheet showing the location of the Dixon’s Ipswich baseline (dark green) to the south of a line (light green) between Flinders Peak and Mount Walker.

 

Given Surveyor General Gregory’s thoughts, detailed above, on the quality of Mitchell/Dixon’s initial baseline and triangulation, it would appear that Gregory wanted a new start. Government Surveyors Robert Hoggan (1852-1929) and Archibald McDowall (1841-1918) thus measured a baseline between Mount Irving and Mount Maria of 7 miles in 1883. Please refer to Figure 31 below. The now Jondaryan baseline (21) was measured using two 100 foot steel bands. Each band was standardised against a steel bar floating in mercury, which itself had been carefully standardised by measurement against the standard bar (OI4) of New South Wales. Three separate readings were taken with each band, so that six independent readings were obtained and could be checked against each other. Overall, the difference between the means of the three measurements from each band amounted to 0.117 inches (3 millimetres). The mean length of the Jondaryan baseline was accepted as 37 029.7549575 feet (7 miles or 11 kilometres). The completion of this baseline then allowed triangulation of a large tract of Queensland; including the Darling Downs, Moreton, Wide Bay, and Burnett districts, stretching south to Wallangarra (beyond Stanthorpe), north to Mount Perry (north of Mundubbera), and eastward to the coast.

 

In mid 1939 then Lieutenant Lawrence FitzGerald (1903-1988), RA Survey used Invar bands to remeasure the Jondaryan baseline as part of a program to consolidate the triangulation in the eastern states. There is more discussion on this aspect later in the paper.

 

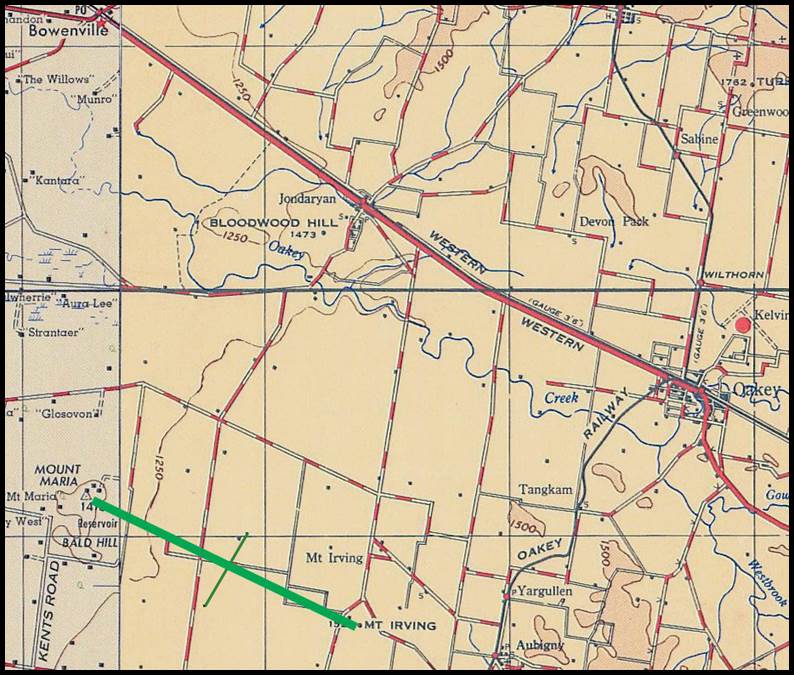
Figure 31 : Section of R502 1: 250 000 scale SG56-14 Ipswich map sheet showing the location of the Jondaryan baseline (approximately east-west, thick green line); the other line is the location of Burnett’s 1849 baseline (approximately north-south, thin green line).

 

The Surveyor General of Queensland then instructed staff surveyor Henry Wood to carry out a triangulation survey of Brisbane city in the late 1880s. A minor baseline of 1 923.748 feet was established, with 100 feet steel bands, along the river bank on the eastern side of the Brisbane Botanical Gardens. Please refer to Figure 32 below. This baseline was measured twice with one of the bands used on the Jondaryan baseline, and once with the other band used at Jondaryan; a fourth measurement was made with a new 100 feet band. A basenet extended from this baseline to finally include the side of a primary triangle formed by the line between Mount Petrie and Eildon Hill. Please refer to Figure 33 below. The length of the Mount Petrie and Eildon Hill baseline (29) was about 9 miles 25 chains. When the length of the minor baseline in the gardens was then computed from the Jondaryan baseline through the intervening primary and city triangulations, in 1889, the length was found to be within 0.01 inches (about 3 millimetres). Triangulation in Queensland was discontinued in 1891.

 

 

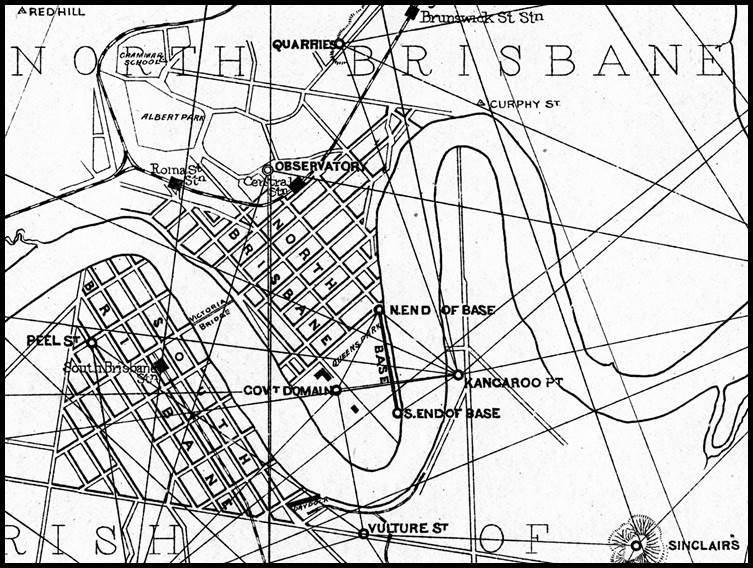
Figure 32 : Section of 1893 map (nla.obj-692765192) Plan illustrating Trigonometrical Survey of Brisbane by R. Hoggan etc, showing the location of the Brisbane CBD minor baseline.

 

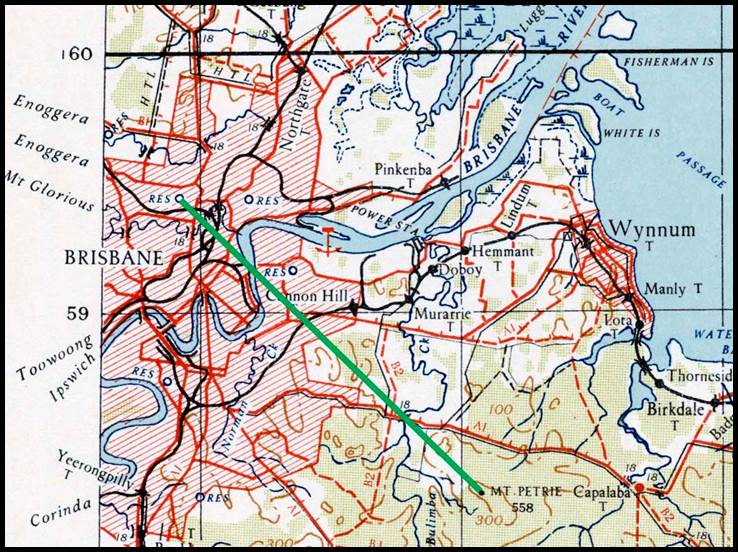
Figure 33 : Section of 1942 1: 253 440 scale SG56-15 Brisbane map sheet showing the location of the Mount Petrie - Eildon Hill baseline.

 

The survey of Brisbane also comprised a standard traverse of South Brisbane made during the first half of 1893, by Cecil Twisden Bedford (1850–1917) and Alan Alfred Spowers (1857-1937), staff surveyors. This standard traverse was run along the main streets, and the stations permanently marked by iron castings set in concrete. The survey was connected with the triangulation survey and was executed with a high degree of accuracy.

 

 

Triangulation Baselines pre 1912

 

Norther Territory of South Australia

Under the administration of South Australia for mapping the positions of gold and tin claims, in 1870, George McKay measured a baseline (15) in the area of McMinns Bluff (after South Australian Government Surveyor Gilbert Rotherdale McMinn) near Pine Creek some 200 kilometres south of Darwin. His survey area reportedly covered an area of 1 000 square miles.

 

By direction of the South Australian Government, a triangulation survey of the MacDonnell Ranges, Northern Territory, was commenced at Alice Springs in 1880. Piles were erected on suitable hills for triangulation stations situated 20 miles west of the telegraph line, and 100 miles east, but detailed observations never reached the head office.

 

Around 1884, David Lindsay (1856–1922) chained the Roper River (22) triangulation baseline somewhere between All Saints Well on the then Overland Telegraph Line in the west and Todds Bluff on the Roper River in the east. His survey area was some 500 square miles.

 

Figure 34 : Map showing the approximate locations of the McKay, Lindsay and Wells baselines in the Northern Territory of South Australia.

 

During the years 1906-1908, Lawrence Allen (Larry) Wells (1860-1938) measured the Victoria River triangulation baseline (33) somewhere between the then Overland Telegraph Line in the east and the eastern boundary of Western Australia in the west. Wells’ survey area was some 20 000 square miles.

 

There is no information about the length of the above baselines or their means of measurement. It is most likely however that they were all measured with a standard 66 feet/100 link chain, the standard measuring apparatus of South Australian surveyors.

 

Based on the information provided above, the approximate locations of the McKay, Lindsay and Wells baselines in the Northern Territory of South Australia are shown at Figure 34 above.

 

 

Triangulation Baselines pre 1912

 

Western Australia

The city of Perth began as the Swan River Colony in 1829, founded largely because the British feared the French would establish a colony in Western Australia. In 1873 the colony of Western Australia was founded.

 

Figure 35 : Map of Western Australia by the Department of Lands and Surveys, showing for 1906-07 the locations of the De Grey baseline and triangulation and Jennaberring baseline east of Perth

(courtesy State Library Western Australia, slwa_b2244687_1.jpg).

 

John Septimus Roe (1797-1878) was the first Surveyor General of Western Australia and in 1829 immediately set about making preliminary surveys of the harbour, river and surrounding land. The sites of Perth and Fremantle were chosen on his recommendation, and he was responsible for laying out these towns. Alongside general settlement, the finding of gold was a driving factor for surveys in Western Australia.

 

The Perth Observatory was connected to the triangulation in July, 1901. The Observatory’s adopted latitude and longitude was then used as the datum for computing the positions of all the triangulation stations in the State. That work involved a complete reduction of all the triangulation surveys and the elimination of differences between baselines and azimuth determinations.

 

Between 1882 and 1887 the essentially coastal triangulation between Fremantle and Geraldton had been observed. The remainder of the triangulation, to the south and north of these locations was then completed by around 1900. The 1911 Department of Lands and Surveys, Map of Western Australia : Showing the Triangulation System, shows triangulation baselines at or near the following localities or on the respective lake beds; Albany, Busselton, Cape Leeuwin, Cervantes, Esperance, Hardman Range (Ord River region), Lake Brown, Lake Deborah, Lake Moore, Marble Bar and Toodyay. The locations of these baselines are shown on the map that may be viewed via this link. At that time, however, it was reported that six baselines had been measured with steel wires 66 feet long; near Perth (23), near Geraldton (24), on the Gascoyne River (25) opposite its confluence with Dalgety Brook, near Globe Hill (26) on the Ashburton River, on the Fitzroy River (27) and near Wyndham (28). The locations of these baselines are shown on the map that may be viewed via this link. The Wyndham baseline was found to have been established by Harry Frederick Johnston (1853-1915, and Surveyor General 1896-1915), between 16 April and 14 May, 1885, on the plain between the East Bastion and Quoin Hills, a distance calculated to be some 9 miles or 14 kilometres. Please refer to Figure 36 below.

 

Figure 36 : Section of R502 1: 250 000 scale SD52-14 Cambridge Gulf map sheet showing the location of Harry Frederick Johnston’s baseline (green line).

 

Doubts arose as to the accuracy of the standard length used by Western Australia around 1902. Two three quarter inch steel bands were subsequently obtained and compared with the British standard and stamped by the British Board of Trade as being of the standard length of 66 feet at a given tension and temperature. One of the bands was then enclosed in a wooden trough in the basement of the main building in Perth, and adapted for accurately testing chains before further use. The second band was carefully stored for use in the case of any accident to the other. The new standard showed a very close agreement with the one previously used.

 

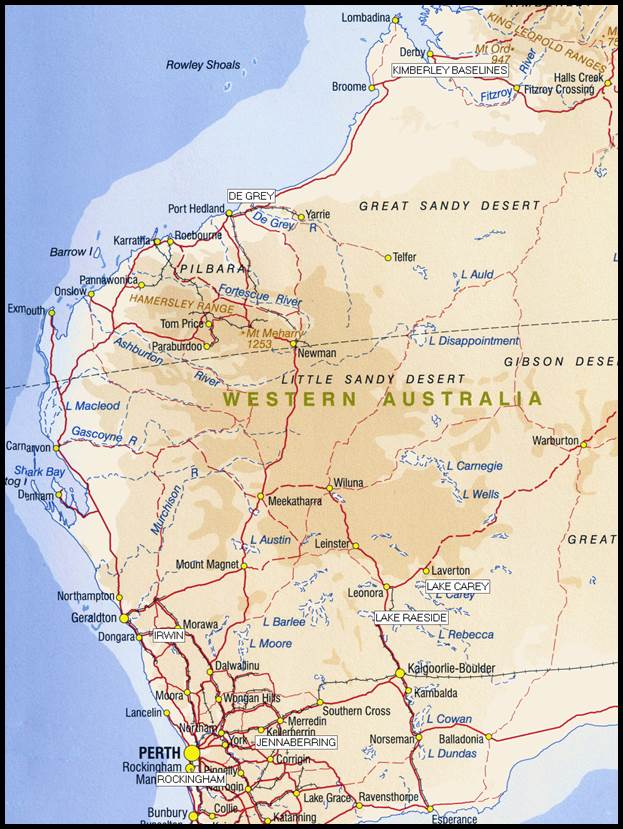
Figure 37 : Map showing the locations of the Western Australian baselines established between 1899 to 1912.

 

Baseline establishment from 1899 to 1912 involved the 1899 triangulation baselines at Lake Carey (30) and Lake Raeside (31). Both baselines were measured with an Invar 500 link band. The survey work covered the nearby Mount Margaret goldfields. Lakes Carey and Raeside and the goldfields are south of the now Leonora-Laverton Road.

 

Three triangulation baselines (32) were measured with an Invar, probably 500 link, band in 1904, 1905 and 1907 in the Kimberley region. The baselines were located east of Derby; one on the Meda River and two, in a quadrilateral arrangement, on the Fitzroy River. These baselines and the earlier Wyndham baseline were all connected by triangulation.

 

The De Grey baseline (34) was measured with an Invar 500 link band in 1906. This baseline was just south of today’s Shay Gap and north of the De Grey river.

 

Nearer to Perth, both the Jennaberring (35) (the location of the Jennaberring baseline is shown in Figure 35 above) and Rockingham (36) baselines were measured using an Invar, probably 500 link, band. In the annual report for the year ending 30 June, 1911, the Surveyor General stated that…An important trigonometrical connection was completed during the year between the coastal triangulation and that carried out by Mr HS King between Mount Bakewell and Mount Stirling in 1890…By means of this connection a comparison was obtained between the Rockingham base measured in June, 1908 and the Jennaberring base measured in August, 1906. The computed values of arc HK 211 to County Peak:- From Rockingham base equals 118,237.76 links; from Jennaberring base equals 118,234.82 links [about 40 miles or 25 kilometres]; difference equals to about 2-10th of a link per mile [0.13 inch/mile or 2 millimetres per kilometre].

 

An Invar 500 link band was used in about 1911 to establish the 48 500 link (6 miles or 10 kilometres) Irwin baseline (37). Apparently named after the nearby Irwin River, the terminal coordinates locate the baseline some 30 kilometres east of Dongara. Please refer to Figure 37 above and Figure 38 below.

 

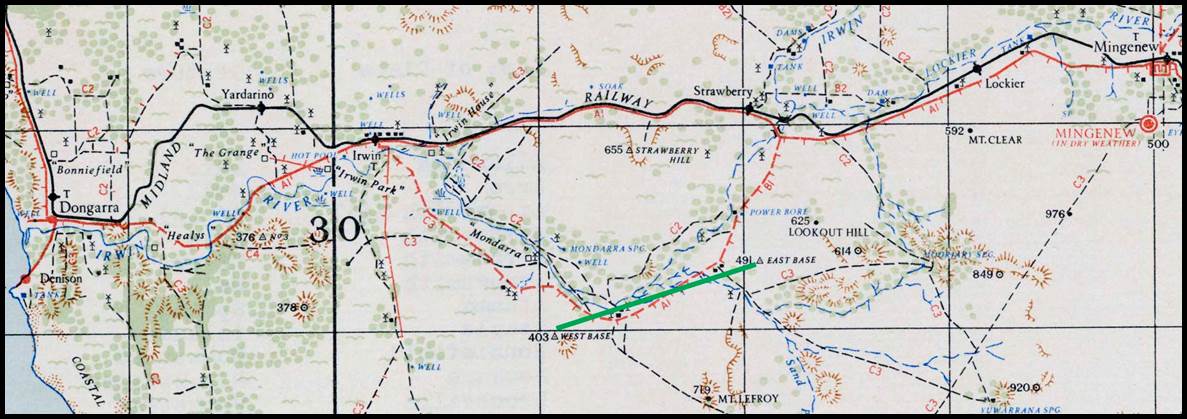
Figure 38 : Section of 1943 1: 253 440 scale SH50-05 Dongara map sheet showing the location of the Irwin baseline.

 

A map showing the locations of the triangulation baselines for the period 1840-1912 and the triangulation work reported by the respective Surveyor’s General at the 1912 conference, may be viewed via this link.

 

 

 

Australian Triangulation Baselines 1912-1929

Following Federation in 1901, the survey and mapping activities within the Commonwealth Government were limited to small scale mapping for aeronautical and general reference purposes whilst the States focussed on the production of mainly cadastral maps for land administration. Thus, topographic mapping in Australia at this time was the exclusive domain of the Army. The Survey Section of the Royal Australian Engineers (RAE) was established in 1910, using the existing State triangulation systems as the control framework for their topographic maps. By 1914 their own geodetic subsection was formed to complete triangulation ahead of the topographers. The Survey Section of the RAE became the Australian Survey Corps in 1915 and subsequently the Royal Australian Survey Corps (RA Survey) in 1948.

 

The first task of RA Survey was a remeasurement of the Werribee baseline in late 1913. It is of interest to note that it was reported that the reasoning for such a remeasurement at that time was unclear. It may have been Ellery’s own statement about wanting to undertake a remeasurement, nevertheless, there appears to be no record of an RA Survey remeasurement ever being completed! The precision of Ellery’s work on the baseline was in the order of 6 parts per million demonstrating a high order of vigilance, given that today’s measurement is 3 parts per million. The associated RA Survey triangulation of some 1 840 square miles (5 000 square kilometres) around Sunbury, north west of Melbourne, was completed in April 1915. Their triangulation then headed west, along a sixty mile (100 kilometre) wide corridor, towards the border with South Australia.

 

In New South Wales, by 1916 their triangulation now extended to Bourke about 300 miles north west of Lake George and although the Bourke baseline had been selected and connected to the triangulation network, it was yet to be measured.

 

 

 

Australian Triangulation Baselines 1920s-1930s

Post war, mapping activity slowly resumed as the servicemen returned. In Queensland the existing triangulation extended from the Darling Downs to the coast near Brisbane. RA Survey took advantage of this existing work to quickly extend a triangulation over some 1 000 square miles on which to base new mapping. To ensure the accuracy of this new triangulation it was determined that a new baseline be established. The 1921 Ipswich baseline (38) was thus established, by men of the survey section of the 1st Military District, on the Normanby Plains near Harrisville, south of Ipswich. As can be seen in Figure 39 below, the 1921 baseline was just east of Dixon’s 1839 baseline described above.

 

Each terminal was marked with a galvanised iron tube 12 inches x 2 inches sunk 3 feet below the surface of the ground. Above the tube was a concrete block 15 inches square, with a brass plug carrying a fine central mark set in flush with the surface of the concrete, the top of the concrete being 1 foot below the natural surface. Above each terminal mark was erected an RA Survey quadrupod.

 

The 10 573 metre (6.7 mile) 1921 Ipswich baseline was measured with Invar bands 5 chains long, standardised against the 66 feet floor standard of the New South Wales Lands Department. Frequent comparisons during the progress of the work were made between the working band and the field standard band. This was satisfactorily achieved by suspending both the working band and field standard band side by side on three supports. Final accuracy of the two way baseline measurement was of the order of 1: 500 000.

 

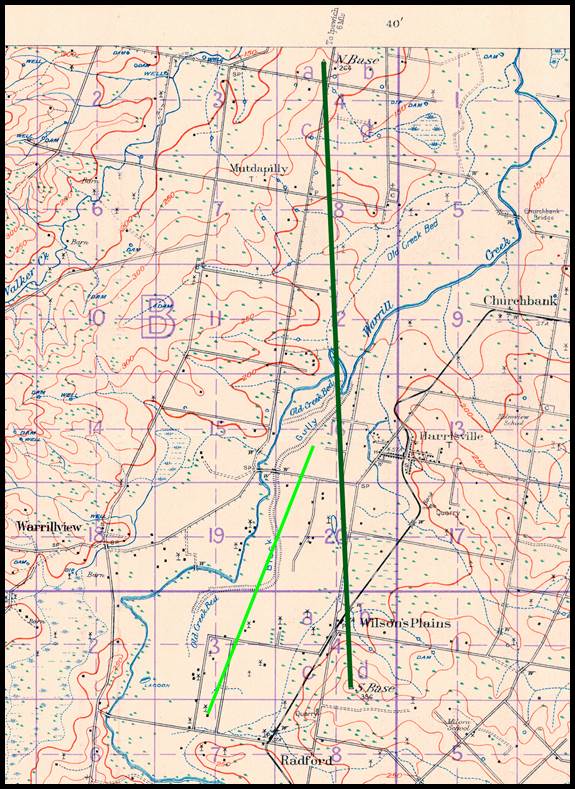
Figure 39 : Section of 1927 1: 63 360 scale SG56 U.IV.SE&SW Flinders map sheet showing the location of the RA Survey’s 1921 baseline (dark green) and just to its west is shown the location of Dixon’s 1839 baseline (light green).

 

In Victoria the mapping focus was now on the Gippsland region to the east of Melbourne. RA Survey first extended a second order triangulation system from the Werribee baseline into South Gippsland in 1930. Earlier in the 1920s, however, mapping was being undertaken by RA Survey around Western Port. Mapping control appears to have come from the 16 236.067 feet (5 kilometres or 3.1 mile) Cora Lynn (39) baseline. The Cora Lynn baseline was established, probably with Invar Band(s), along the Koo-Wee-Rup main drain in 1926 (this drain was integral to a massive swamp drainage project which turned a swamp area into rich farming land; alongside the drain’s straight, long section of some 10 miles, which has Cora Lynn at its approximate centre, would have been ideal for a baseline. Please refer to Figure 40 below. As is detailed later, when a check was required on the Victorian Geodetic Triangulation network the Cora Lynn baseline was integrated into the surrounding triangulation.

 

In the period, post World War One to the end of 1931, sixty 1: 63 360 scale map sheets had been surveyed with triangulation control, mapped and published.

 

By 1932, the first order, Sydney-Melbourne triangulation network had been extended south from around Albury into the Latrobe Valley. It would appear that the Morwell baseline (41) of 2.7 kilometres or 1.7 miles, was established before or during this period to control this southern triangulation extension. Please refer to Figure 41 below. In 1942 a triangulation network, to second order standards, expanded the existing southern Victorian coastal triangulation as far east as Wilsons Promontory.

 

Figure 40 : Section of 1943 1: 253 440 scale SJ55-10 Warragul map sheet showing the location of Cora Lynn and the Koo-wee-rup main drain alongside which RA Survey established their 1926 baseline.

 

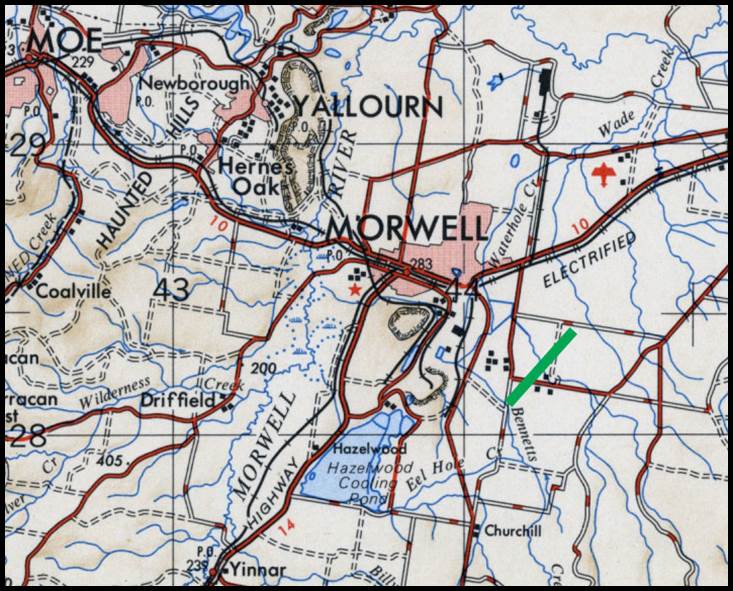
Figure 41 : Section of R502 1: 250 000 scale SJ55-10 Warragul map sheet showing the location of the Morwell baseline.

 

This work however highlighted the problem found by Victoria in 1870 during its work to fix the Black-Allan Line to mark the straight line border section between New South Wales and Victoria; the geographic coordinates of points calculated from the New South Wales triangulation based on the origin of the Sydney Observatory were different (enough to be of concern in a first order survey) from the geographic coordinates of points calculated from the Victorian triangulation based on the origin of the Melbourne Observatory. At this time RA Survey was in the process of producing the across border, Albury 1: 63 360 (1 mile to 1 inch published in 1933) scale map sheet and this work could not proceed until a resolution to the mismatched coordinate problem had been found.

 

An examination of the Victorian triangulation records found that in places this survey was not to a first order geodetic standard. A recomputation and rigorous adjustment of a series of well conditioned triangles through the Victorian triangulation network to the Werribee baseline was thus undertaken. Please refer to Figure 42 below. A braced, cross border quadrilateral was used to compare the New South Wales and Victorian derived coordinates carried through the Victorian network. Further, the triangulation computations were extended to include a comparison with the RA Survey’s Cora Lynn baseline.

 

The result indicated that rather than the quality of the Victorian triangulation being at fault, the coordinate differences occurred; firstly, due to the Melbourne and Sydney Observatories being on independently obtained astronomical origins; and secondly because the respective colonies used different figures of the earth for their computations as listed below.

 

 

Figure 42 : Section of 1: 5 000 000 scale map showing the Victorian triangulation stations used in the recomputation and rigorous adjustment of the network; the stations of the braced, cross border quadrilateral are shown in green; note that for clarity not all observed lines are shown in the vicinity of the Werribee baseline (yellow - refer Figure 23 above) and the line Flinders Peak-Williamstown is bent; the location of the Cora Lynn baseline in relation to this network is also shown.  

 

This analysis led to a number of decisions. Firstly, the geographic coordinates of the Sydney Observatory were adopted as the origin for geographical coordinates for eastern Australia (this origin remained until the 1966 adoption of the Johnson Geodetic Origin); secondly was the adoption of Clarke's (1858) Figure of the Earth as the common mathematical base for geodetic coordinates; and lastly, the improvement of existing triangulation surveys by reobservation or recalculation, and the measurement of another baseline in the vicinity of Mount Gambier in South Australia to provide a triangulation verification baseline further west.

 

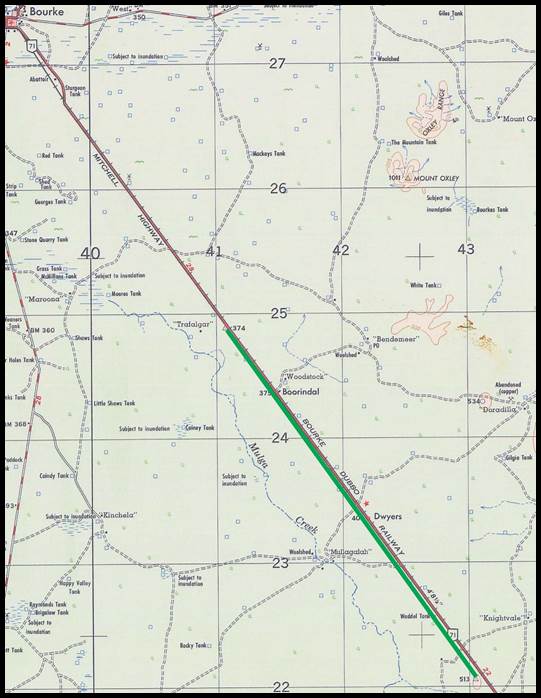
Figure 43 : Section of R502 1: 250 000 scale SH55-10 Bourke map sheet showing the location of the Bourke baseline (green line).

 

The Lands Department of New South Wales undertook the measurement of the Bourke triangulation baseline (40) in 1927. Please refer to Figure 43 above. Although six 24 metre Invar bands had been received in 1911 after standardisation at the National Physical Laboratory, England, two bands were returned for restandardisation. Four bands were thus used for the baseline measurement of just over 19.6 miles. From the recorded temperatures it appears that the measuring operations were undertaken at night when atmospheric conditions were most stable. In all, it took over 2600 sets of 24 metre measurements to complete the observations. Measuring operations commenced at the north end with the field party members being Surveyor General Hamilton Bartlett Mathews, Staff Surveyor Frederick Charles Della Ca, and two other professional officers with field assistant Arthur W Bonner and a further three field hands. Computations were completed by HE Messer (Computer, Trigonometrical Branch). On 26 March 1931, Staff Surveyor Della Ca reported that a roll plan (927-3015) had been prepared and forwarded to Surveyor General Mathews showing the details relating to the measurement and marking of the Bourke baseline.

 

Comparisons from Lake George to Bourke Base taken partly through single triangles gave an unadjusted difference of 4.92 feet or 1 part in 21 000, between the measured and the computed length of the Bourke Base. In view of the discrepancy, but essentially for the purpose of establishing a first order triangulation network throughout an area extending north east to the main triangulation network near Tamworth, a new baseline was to be created at Condobolin. World events caused the major delay in those plans until 1945.  

 

In 1927 the Richmond baseline was remeasured with Invar band(s). The misclose between the 1879 measurement at Richmond, made with wooden bars and also steel rods as the measuring apparatus, and the later 1927 measurement with Invar was 0.2709 feet (83 millimetres) or about 1 part in 13 600. The Richmond Base measurements were intended partly for training personnel in the use of new equipment brought into the country for the Bourke Baseline and partly for the comparison with Conder's [1881] value.

 

Figure 44 : Section of R502 1: 250 000 scale SJ54-06 Penola map sheet showing the location of the Millicent (also Cave Range or Mount Gambier) baseline.

 

A location for the Mount Gambier baseline was found in October 1933, by RA Survey. The site at Cave Range, being just outside Millicent, South Australia, this baseline became more commonly known as the Millicent baseline (42). Please refer to Figure 44 above. In March 1934, Invar bands, 5 chains long, standardised against the 66 feet floor standard of the New South Wales Lands Department, were used to measure the 4.6 mile (7.4 kilometre) Millicent baseline. In May 1934 a further baseline of 4.7 miles (7.6 kilometres) was measured by RA Survey, near Tarlee (43), about 80 kilometres north of Adelaide. Please refer to Figure 45 below. Again, Invar bands, 5 chains long, standardised against the 66 feet floor standard of the New South Wales Lands Department were used for this work. The triangulation network of some 300 miles (500 kilometres) connecting the Millicent and Tarlee baselines was then observed to first order standards by RA Survey. A uniform triangulation network now existed from Albury, via the Werribee and Millicent baselines to Tarlee.

 

                             

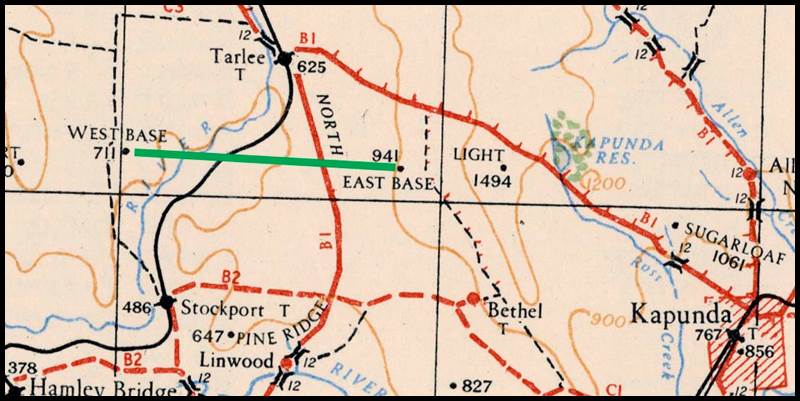
Figure 45 : (Left) Section of 1942 1: 253 440 scale SI54-09 Adelaide map sheet showing the location of the Tarlee baseline;

(Right) Original Tarlee East Base centre pole and vanes at Riverton Museum (courtesy Bill Stuchbery).  

 

To now expand, and provide a check on the New South Wales triangulation from north of the Richmond baseline for a further 500 kilometres north into Queensland and connect it to the Jondaryan baseline a new baseline site was found by RA Survey, at Somerton (45) near Tamworth in 1936 (being on the Manilla map sheet the Somerton baseline may sometimes be referred to as the Manilla baseline). Please refer to Figure 46 below. The terminals of the 28 239.17308 feet (5.3 mile or 8.6 kilometre) Somerton baseline, consisting of an RA Survey plaque set in an observing pillar with quadrupod beacon, were then established in 1937.

 

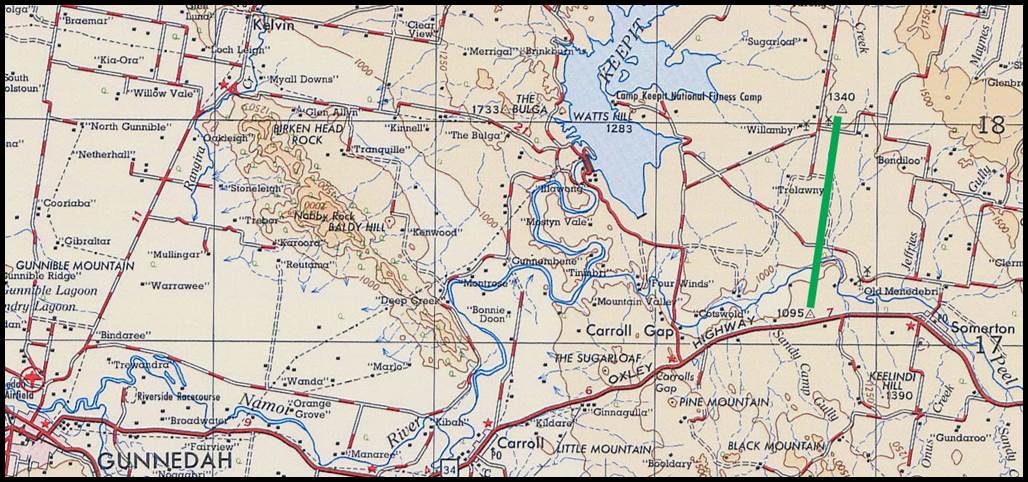
Figure 46 : Section of R502 1: 250 000 scale SH56-09 Manilla map sheet showing the location of the Somerton baseline in green.

The location of this baseline as depicted in the section of the combined County of Mitchell, Parish of Bullenbung and County of Mitchell, Parish of Ashcroft map sheets, may be viewed via this link.

 

A further baseline was also sited in late in 1938 at Benambra (46) in Victoria to the north of Omeo. Please refer to Figure 47 below.

 

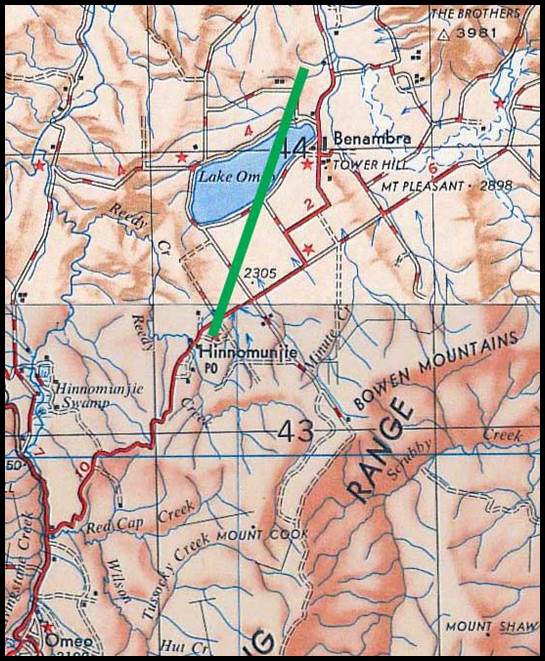
Figure 47 : Section of R502 1: 250 000 scale SJ55-03 Tallangatta map sheet showing the location of the Benambra baseline in green.

 

Measuring the Benambra baseline (after Fitzgerald, 1948).

 

For the first six months of 1939, RA Survey observed a triangulation network to first order standards, north eastwards from the Benambra baseline towards Mount Pilot and Mount Kosciuszko in New South Wales. As the winter months approached the triangulation survey was redirected to connect to the triangulation out of the Werribee baseline. In July-August 1939, the RA Survey then undertook the latest measurement of the Jondaryan baseline, followed by measurement of the Somerton baseline in September 1939. Both these baselines were measured using 4 Invar bands, 50 metres long and RA Survey’s resistance thermometry technique.

 

The original terminal mark on Mount Irving terminal of the Jondaryan baseline was found damaged, but was carefully re-established to within a couple of millimetres. The 1939 measurement was found to be some 4 inches shorter than the 1883 measurement supporting Queensland’s belief that the value attributed to the Queensland standard bar in 1883 was too high. Nevertheless, the earlier work was of a very high standard being better than 10 millimetres in 1 kilometre.

 

Triangulation, to first order standards, connecting these bases now extended from Queensland, via New South Wales and Victoria, to South Australia. This network was completed in March 1940 with the measurement of the of 5.9 mile (9.5 kilometre) Benambra baseline, across the then dry lakebed of Lake Omeo.

 

Figure 48 : Section of R502 1: 250 000 scale SF53-09 Napperby map sheet showing the location of the Ryan Well baseline.

 

Terminal coordinates were found for a baseline at Ryan Well (44), Northern Territory. The 6 mile (10 kilometre) baseline was sited some three kilometres to the east of Aileron on the Stuart Highway, about 135 kilometres north of Alice Springs. Please refer to Figure 48 above. The Ryan Well baseline was some 6 kilometres north of the Ryans Well Historical Reserve containing the 1889 hand dug well, by Ned Ryan, used to supply water to travellers and stock along the Overland Telegraph Line. The reserve also contains the Glen Maggie Homestead ruins. The Nicker family built the Glen Maggie sheep and cattle station near the well in 1914 and charged a small fee per head to draw water for travelling stock. By 1921 the homestead also served as a telegraph office and store. In 1932 it was a renowned last stop for supplies for miners heading north west to The Granites gold rush. The building was finally abandoned in 1935 and the Telegraph Office was moved north to Aileron Station.

 

Figure 49 : Nat Map observer at Central Mount Stuart, 1957 (courtesy Ed Burke).

 

With only the terminal coordinates the date and reason for the Ryan Well baseline is uncertain. Triangulation work in the Ryan Well area was not reported in 1912 and post World War Two the national triangulation bypassed it. However, records show that when the national triangulation network came through this region in 1957 the then occupied heights were already marked with earlier beacons. These older, circa mid 1930s beacons, reportedly erected by the Lands and Survey Department, Northern Territory, were thus upgraded as part of the 1957 triangulation. The circa mid 1930s Lands and Survey Department, Northern Territory, triangulation only established beacons as far north of Alice Springs as the vicinity of Barrow Creek (a distance of some 300 kilometres). This triangulation did however, include the 900 metre high peak of Central Mount Stuart. Please refer to Figure 49 above. Hurren (1959) recorded that a triangulation survey of about 12 000 square miles was completed in the Alice Springs area in about 1937 by Surveyors Augustus James Blakeway (1886-after 1937), John Henry Driver (1902-1960) and Frank Pettinger Shepherd (1901-1939, Surveyor General of the Northern Territory, 1932-1938) of the Northern Territory Administration. The angular work was to about second order standard but the baseline measurement was of a much lower order. Most of the stations were marked with permanent ground marks which were covered by rock cairns. With no other evidence, it would therefore seem that the Ryan Well baseline was established as part of the 1937 triangulation. Such a date would also tie into the historical account above as it may have been established with the aim of pastoral and mining lease control. Due to the lack of reliable water, however, these requirements were only ever fleeting.

 

It should be noted that between 1945 and 1947 some 400 miles of precise geodetic survey was completed along the Stuart Highway north from Alice Springs. The survey was undertaken by the Lands and Survey Section of the Northern Territory Administrative Branch of the Department of the Interior. In 1957 when the national triangulation survey was in this area Ford (1979) stated…several connections were made to the Stuart Highway Traverse (a high quality ground traverse from Alice Springs to the vicinity of Muckaty Bore). Ford’s reporting of connections to the road traverse and not to the Ryan Well baseline appears to indicate that the Ryan Well baseline was not a crucial element to the national triangulation survey.

 

A map showing the location of the Ryan Well baseline relative to the Stuart Highway survey, shown as the green line, and the national geodetic triangulation stations (blue triangles) may be viewed via this link. The two locations, K100 and R602, where survey connections were made from the national geodetic triangulation to the Stuart Highway survey, are also indicated.

 

 

 

Australian Triangulation Baselines 1940s

RA Survey established the Carrieton baseline (47) of 4.3 miles (7 kilometres) in 1941. Please refer to Figures 50 and 51 below. Carrieton is some 100 kilometres almost due east of Port Augusta, South Australia, and over 200 kilometres north of the baseline at Tarlee. As can be seen in the photograph at Figure 51(left) of the station it consisted of an RA Survey plaque set in an observing pillar with quadrupod beacon.

 

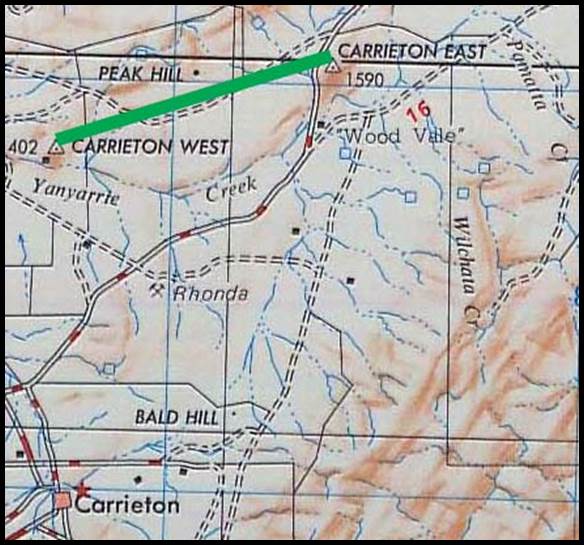
Figure 50 : Section of R502 1: 250 000 scale SI54-01 Orroroo map sheet showing the location of the Carrieton baseline.

 

           

Figure 51 : (Left) Carrieton baseline, western terminal observing pillar and (Right) view to eastern terminal, 1968 (courtesy Adrian Wright).

 

Australia’s defence now became top priority. Triangulation and associated baselines for the control of topographic maps would be undertaken to second order standards. For small areas, removed from the triangulation networks, the mapping control would be provided by astronomic observations and requisite local survey. During this period the following baselines were established :

 

Queensland around Townsville and Cairns

In the first half of 1942, mapping was required around Townsville as no topographic mapping then existed. The Townsville baseline (48), to second order accuracy, of over 3 miles (5 kilometres), please refer to Figure 52 below, was established and extended by triangulation to cover the Townsville region. The next priority was the Cairns region. Again, a baseline, to second order accuracy, reportedly of 7 000 feet, to the north of Gordonvale (49)(please refer to Figure 53 below), was established. Gordonvale was some 20 kilometres south of Cairns, and this baseline provided local map control for the coastal mapping. Mapping in the Atherton Tablelands followed where a further baseline was measured at Kairi near Atherton, some 50 kilometres west of Cairns. The Kairi baseline (50) had a length of about 1.5 miles (2.5 kilometres). Please refer to Figure 54 below. A basenet at Kairi using the silo at Tolga and a basenet at Gordonvale using the heights of Base Extension and Walshs Pyramid provided a connection between the two schemes being Tolga Silo–Walshs Pyramid. This connection (not all observed lines shown) may be viewed on this map. These mapping triangulation schemes were later integrated into the Townsville-Cairns-Cooktown triangulation.

 

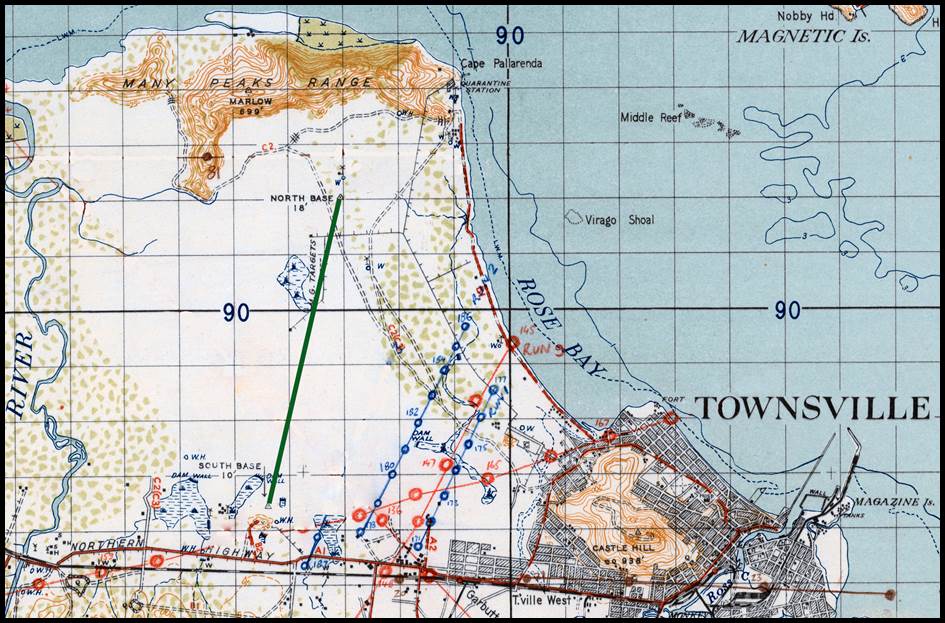
Figure 52 : Section of 1942 1: 63 360 scale Townsville (Special) map sheet showing the location of the Townsville baseline (thick green) about where the airport is today (note the map has other pencil annotations in blue and red.

 

Figure 53 : Section of 1942 1: 63 360 scale No.57 Zone 7 Gordonvale map sheet showing the location of the Gordonvale baseline (green) along today’s Highleigh Road with its western terminal near Crossland Road.

 

Figure 54 : Section of 1942 1: 63 360 scale No.57 Zone 7 Gordonvale map sheet showing the location of the Kairi baseline (green) with the southern terminal at Kairi Silo.

 

Northern Territory at Adelaide River

The 3 mile (4.9 kilometre) Adelaide River baseline (51) was used by RA Survey to fix the control required for the Adelaide River 1:  253 440 scale map released in 1942. Please refer to Figure 55 below.

 

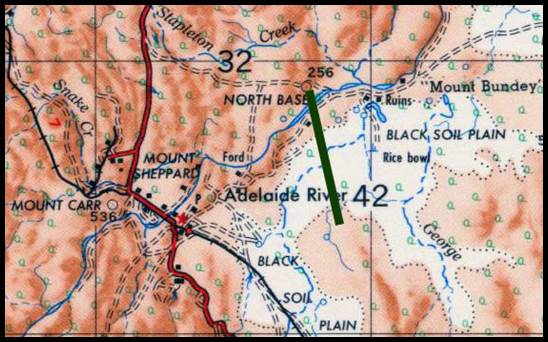
Figure 55 : Section of R502 1: 250 000 scale SD52-08 Pine Creek map sheet showing the location of the Adelaide River baseline in green.

 

Queensland at Bowen

The 1.8 mile (2.8 kilometre) Bowen baseline (52) was used by RA Survey for local mapping. Please refer to Figure 56 below.

 

Figure 56 : Section of R502 1: 250 000 scale SF55-03 map sheet showing the location of the Bowen baseline in green.

 

Queensland at Iron Range

The Iron Range survey control consisted of two baselines (53) in the form of an ‘X’ as can be seen in Figure 57 below. The longer approximately east-west baseline was 1.6 miles (2.6 kilometres) long while the approximately north-south baseline was 1.5 miles (2.5 kilometres) in length. They were used by RA Survey to fix the control required for local survey and mapping of the Iron Range area. The terminal stations were each marked with a shell casing set in a concrete block. It was recorded that on 30 May 1942 a ground survey of Iron Range was undertaken for suitable airfield sites. Construction of an airfield for use by heavy bombers was begun by United States Army Engineers in June 1942 and completed by the Queensland Main Roads Commission for the Allied Works Council. United States bombers were operating from Iron Range by September 1942. The three airstrips at Iron Range were constructed between mid 1942 and 1944.

 

Figure 57 : Section of R502 1: 250 000 scale SD54-04 Cape Weymouth map sheet showing the location of the Iron Range baselines in green.

 

Queensland at Cape York

The 1942, 1.2 mile (2 kilometre) Cape York baseline (54) was used by RA Survey to fix the control required for local survey and mapping of the Cape region. The terminal stations were each marked with an RA Survey plaque set in a concrete block with quadrupod beacon. The Orford Bay 1: 253 440 scale map sheet published in March 1944 states that control was by astrofix and traverse. The Thursday Island 1: 253 440 scale map sheet published in May 1943 covering Cape York contains no specific map control information. Please refer to Figure 58 below.

 

Figure 58 : Section of R502 1: 250 000 scale SC54-12 Torres Strait map sheet showing the location of the Cape York baseline in green.

 

Queensland at Cooktown

The 3.4 mile (5.4 kilometre) Cooktown baseline (56) ran from near the local airport to the west along the railway line. Established in 1944, it was used to control the northern extension of the Townsville-Cairns triangulation. Please refer to Figure 59 below.

 

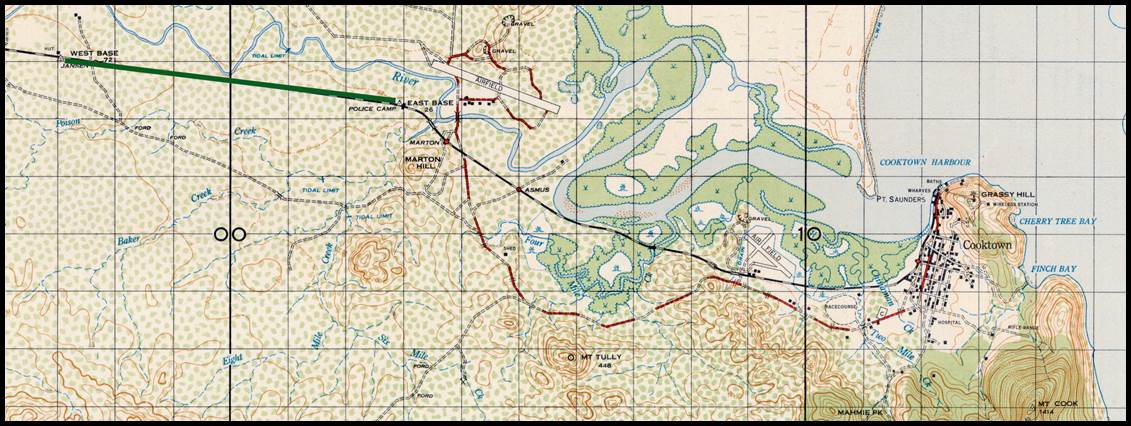
Figure 59 : Section of 1946 1: 63 360 No.26 Zone 7 Cooktown map sheet showing the location of the Cooktown baseline in green.

 

Figure 60 : Map showing the locations of the baselines established along the northern Queensland coast, 1942-1944.

Triangulation in Western Australia after 1941, essentially supported the required mapping activity. Specifically, the existing Western Australian Lands Department triangulation was extended, to second order standards, from Perth north and south generally along the coastal fringe. To the south, triangulation networks were completed from Perth to Bunbury and Perth to Albany; to the north a triangulation network was completed from Perth to Geraldton. Baselines are recorded as having being established as described below :

Western Australia at Gascoyne Junction

The 7.3 mile (12 kilometre) Gascoyne Junction baseline (55) was some 7 kilometres south west of Gascoyne Junction, and some 150 kilometres east of Carnarvon. Established in 1942 it formed part of the control for wartime mapping of the coastal fringe in the Carnarvon region. Please refer to Figure 61 below.

 

 Figure 61 : Section of R502 1: 250 000 scale SG50-05 Wooramel map showing the location of the Gascoyne Junction baseline in green.

 

Western Australia at Roebourne

The 3.6 mile (5.8 kilometre) Roebourne baseline (57) was just east of Roebourne. The two terminal stations were only marked with an RA Survey plaque set in a concrete block. Established around 1944 it formed part of the control for wartime mapping of the coastal fringe around Port Hedland. Please refer to Figure 62 below.

 

Figure 62 : Section of R502 1: 250 000 scale SF50-03 Roebourne map sheet showing the location of the Roebourne baseline in green.

 

A triangulation network, to second order standards, was begun in 1939 starting at the Jondaryan baseline, to run north towards Rockhampton to provide the necessary mapping control for that region. During 1942, the triangulation section between Maryborough and Rockhampton was completed and with later work along the McPherson Range, the border range between Queensland and New South Wales. Post war, the triangulation network was taken west from Rockhampton to Emerald where it turned north to Clermont, for the standard mapping of the Emerald and Anakie areas. The Rockhampton-Clermont triangulation was reported complete by 1955. Later it was reported that by 1960 a triangulation, to first order standards, had been completed between Clermont and Mount Coolon to the north. A triangulation network extending north from Rockhampton to connect with the existing network around Ayr was discontinued before completion.

 

The observation of a Western Australian triangulation network, to second order standards, from Perth to Albany approximately following the route of the Albany Highway was being progressed. By 1945 it was reported that this triangulation had reached the vicinity of the town of Williams on the highway but had by now been extended to the north of Perth along the coast as far as Geraldton. By 1955 this triangulation network had been completed to Albany.

 

The number of 1: 63 360 scale topographic map sheets, mostly based on baselines and triangulation, had now increased significantly as can be seen in the following table.

           

Year	Total number of 1: 63 360 scale topographic map sheets produced
1931	60
1939	80
1945	342

 

A remeasurement of the Richmond Base was carried out in 1944 by the same personnel of the Lands Department of New South Wales who had earlier undertaken the 1927 measurement of the Bourke triangulation baseline.

 

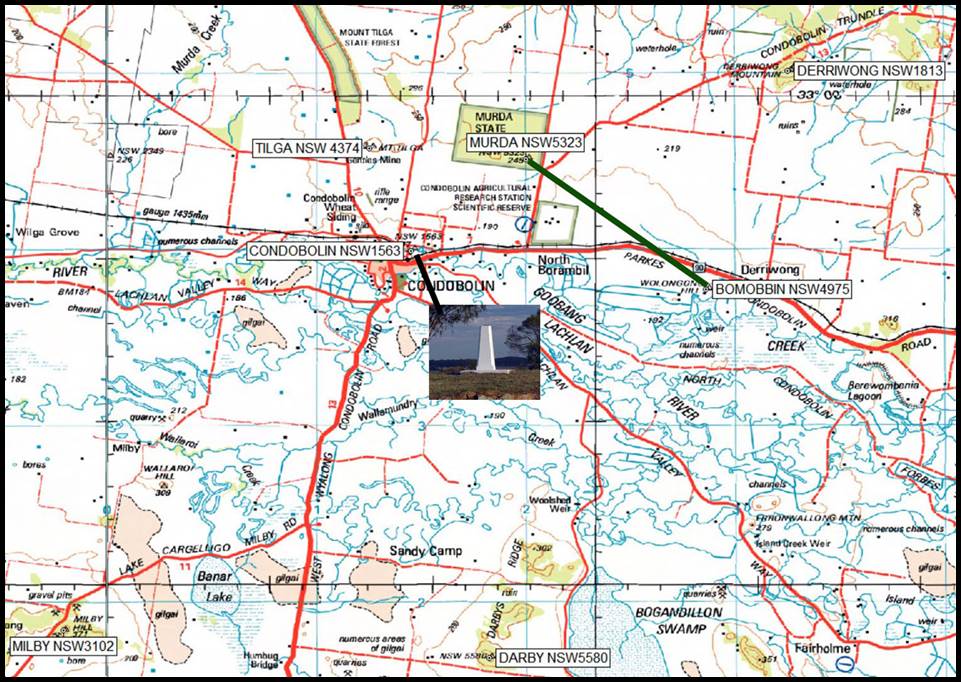
Figure 63 : Section of NTMS 1: 250 000 scale SI55-07 Forbes map sheet showing the location of the Condobolin baseline in green and the surrounding primary basenet stations; a photograph of the Condobolin Astronomic Station pillar in the town itself is shown as an insert; the distance Derriwong to Milby is about 30 miles.

The location of this baseline as depicted in the section of the County of Cunningham, Parish of Wollongong map sheet, may be viewed via this link.

 

Figure 64 : Section of New South Wales Topographic 1: 50 000 scale 8331-N Condobolin map sheet showing station NSW4975 Bomobbin sited on Wolongong Hill.

 

A fifth New South Wales baseline was measured, and a basenet observed by Lands Department surveyors in 1945. The 7.1 mile (11.3 kilometre) Condobolin baseline (58), just north of the town, followed the earlier baselines at Lake George, Richmond, Bourke and Somerton (Tamworth). Please refer to Figure 63 above showing the Condobolin baseline had Mount Murda (NSW5323) and Bomobbin (NSW4975) as its terminals. Figure 64 above, shows that today Bomobbin (NSW4975) is sited on Wolongong Hill. A published interview from 1945, with the survey party leader Charles Edward Elphinstone (1898-1965, and later Surveyor General 1960-1963) is at Annexure F.

 

Invar bands, 24 metres in length were used to measure the baseline. While the exact number of bands used was not found, six 24 metre Invar bands had been received by New South Wales, in 1911. The bands used at Condobolin had, however, been previously standardised by the Science Laboratory at Teddington, London and great care is taken to preserve this standard of length by the Lands Department of New South Wales. Two measurements of the baseline agreed to within an eighth of an inch (about 3 millimetres). From the baseline terminals a series of 22 triangles were then observed in order to extend the base length to three of the primary triangle sides about thirty miles long.

 

As part of the triangulation around Condobolin the triangulation station of Condobolin, located within the town, was incorporated. As far back as the late 1880s this point had been geographically fixed by astronomic determinations for latitude and longitude. For the geodetic survey of Australia this same point had been the location for a Laplace Observation. Thus in 1945 similar observations were likely made using the equipment of the day.

 

A new computation based on the Lake George baseline gave a misclose on the Condobolin baseline of 1 part in 32 000 and from the Condobolin baseline to the Bourke baseline a misclose of 1 part in 29 600 was achieved.

 

RA Survey provided mapping assistance to the then Bureau of Mineral Resources in the late 1940s. To provide the mapping control a triangulation was undertaken along the Fitzroy River approximately between Fitzroy Crossing and Halls Creek but extending some distance to the west and east of both those towns. Some 15 kilometres south east of Fitzroy Crossing the Noonkanbah baseline (59) was established in 1947 to control the triangulation. Please refer to Figure 65 (top) below. The Noonkanbah baseline north-south distance was 4.2 miles or 6.7 kilometres. From this control work the SE51-12 Noonkanbah, 1: 253 440 scale map sheet was produced. The modern NTMS at Figure 65 (bottom) shows the Noonkanbah baselines are now in the form of a triangle with a north, south and east terminal (note that the south terminal is in a different location to its 1947 position and the north-south distance is 4.7 miles or 7.5 kilometres, south-east distance is 4.2 miles or 6.8 kilometres). It is uncertain if all three lines were measured to baseline standards. All three terminal stations were marked with a precast concrete block set with a centre point with a quadrupod beacon.

 

Figure 65 : (Top) Section of 1950 1: 253 440 E51-12 Zone Noonkanbah map sheet showing the location of the Noonkanbah baselines in green.

 (Bottom) Section of NTMS 1: 250 000 scale E51-12 Noonkanbah map sheet showing the location of the Noonkanbah baselines in green.

 

 

 

 

Australian Triangulation Baselines 1950s

Post World War Two RA Survey had become involved with the survey work necessary to support the activities of the Woomera Rocket Range. By mid 1950 sufficient work had been completed to connect the triangulation work carried out on the range with the triangulation network extending from Carrieton west to Mount Eba near Kingoonya. A decision was made to establish a baseline at Koolymilka (60), some 40 kilometres north west of the township of Woomera. Please refer to Figure 66 below. The Koolymilka baseline, situated some 6 miles north west of Lake Koolymilka, was 7.1 miles long (11.5 kilometres) between terminal stations Knoll to the north and Boundary to the south. The baseline was measured during July and August 1950, using 4 Invar bands, 50 metres long and RA Survey’s resistance thermometry technique. At Knoll the station mark was a brass shell case set in concrete with a quadrupod beacon, while at Boundary the station mark consisted of an RA Survey plaque set in concrete with quadrupod beacon. This baseline was the last RA Survey triangulation baseline established by chaining.

 

The later 1955, 3.2 mile (5.2 kilometre) Mildura baseline (62), although established by chaining likely with Invar band(s), was only used by RA Survey to fix the control required for the Mildura 1: 50 000 scale map released in 1955. Please refer to Figure 67 below. In 1957 RA Survey established a 3.4 mile (5.5 kilometre) baseline (63) near Wyndham, Western Australia but the records appear to indicate that it was measured by Tellurometer. Please refer to Figure 68 below.

 

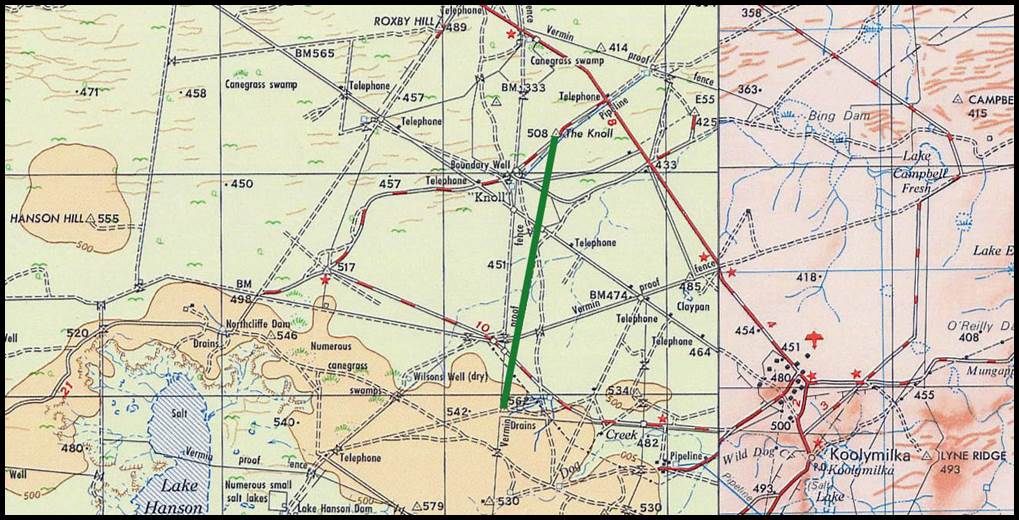
Figure 66 : Section of combined R502 1: 250 000 scale SH53-11 Kingoonya and SH53-12 Andamooka map sheets showing Koolymilka baseline in green between stations Knoll to the north and Boundary to the south.

 

Figure 67 : Section of R502 1: 250 000 scale SI54-11 Mildura map sheet showing the location of the Mildura baseline in green.

 

Figure 68 : Section of R502 1: 250 000 scale SD52-14 Cambridge Gulf map sheet showing the location of the 1957 Wyndham baseline in green.

 

By the end of 1945 the then Prime Minister John Curtin (1885-1945) had not only obtained the agreement of the State Premiers to a coordinated national mapping program and the formation of a National Mapping Council (NMC), but the NMC had held its first meeting. However, it was not until 1954 that the new National Mapping agency had the resources to commence triangulation in its own right. Priority needed to be given to meeting the Bureau of Mineral Resources mapping requirements by completing a triangulation scheme in the area around Broken Hill and the Barrier Range.

 

At that time the Broken Hill area was isolated from any existing triangulation chains; the two nearest schemes being the RA Survey primary triangulation in the Peterborough - Orroroo - Carrieton area of South Australia and the New South Wales Lands Department triangulation near Cobar. The Broken Hill scheme would thus need to incorporate a classical baseline and basenet triangulation to expand the measured base. However, back in 1948 the then Deputy Director of National Mapping, Bruce Lambert, saw a demonstration of the Geodimeter the first distance measuring equipment which could provide distance measurements of a suitable accuracy for geodetic survey. National Mapping had placed an order for a Geodimeter in 1953 and the equipment was expected by mid 1954. If the Geodimeter proved itself basenet schemes would be a thing of the past as a side or sides of triangles in the triangulation could now be measured directly.

 

Figure 69 : Section of R502 1: 250 000 scale SH54-15 Broken Hill map sheet showing the location of the proposed Broken Hill baseline.

 

Figure 70 : South terminal of the Broken Hill baseline showing the steel star rod in concrete, protected by its steel enclosure with lid.

 

Just in case the Geodimeter did not meet expectations a basenet scheme was established in 1954, with the two terminal stations being steel star rods in concrete blocks. Please refer to Figure 69 above. These two sites were later protected with steel enclosures with lids. Please refer to Figure 70 above.

 

Howard Angas (Bill) Johnson (1907-1990), was now Senior Surveyor in charge of National Mapping’s Geodetic Surveys. Johnson had just left the Army where he had been a Lieutenant Colonel and Chief Instructor at the Army School of Military Survey. Previously in 1939, Johnson had been closely involved with RA Survey’s measurements of the Jondaryan (Queensland) and Somerton (New South Wales) triangulation baselines. This knowledge of the site and measuring manpower and equipment requirements would thus have been applied to the selection of the baseline site at Broken Hill, and partly to the decision to not immediately measure the baseline.

 

The available resources went into the observations of the triangulation to connect with the RA Survey’s triangulation near Carrieton. This plan enabled preliminary coordinates on the Sydney datum to be calculated immediately for the stations in the Broken Hill area, and allow the required mapping to proceed. As is discussed later in this paper the Geodimeter’s performance was to specification. The outcome was that the planned Broken Hill baseline (61) of 4 892 metres was never physically measured. The Geodimeter was used to measure a side of one of the triangles observed and this alternative baseline was used for the final adjustment and calculations.  

 

A map showing the locations of the triangulation baselines for the period 1920s-1950s, essentially established for local mapping control, may be viewed via this link.

 

A map showing the locations of the triangulation baselines for the period 1920s-1950s and the triangulation work as documented in reports of the National Mapping Council and described in various sources, may be viewed via this link.

 

 

 

Australian Triangulation baselines in the Geodimeter era

From August 1954 until March 1956 the Geodimeter was employed to measure various baselines in Victoria, New South Wales, South Australia and Queensland. For the most part the Geodimeter had no trouble in measuring lines up to 15 kilometres and if everything went right up to 25 kilometres but this was only achieved once. Accuracy was of the order of 1 part in 200 000 or an error in the distance measured equivalent to 5 millimetres for every kilometre. Such accuracy was comparable to that obtained by any high precision baseline Invar chaining. Overseas tests had produced results that were accurate to 1 part in 300 000. Lambert in his 1956 paper The Geodimeter and its Uses quoted the error of the mean of two night’s [Geodimeter] measurements is not greater than ±0.3±(distance / 1 000 000) feet, with a note indicating that the manufacturers were modifying the equipment to eliminate most of the fixed instrumental error.

 

Figure 71 : Circa mid-1950s photograph of a Geodimeter, NASM-2, in use in Western Australia by the Western Australia Lands Department (courtesy Landgate).

 

In June 1956, a new Geodimeter was tested by National Mapping before being loaned to the Western Australia Lands Department. Lands Department Surveyor William Thomas (Tom) Meharry travelled from Perth to Melbourne and was trained to use the Geodimeter. After returning to Western Australia with the instrument it was used by Meharry in December 1956 in the south west region of Western Australia from Bunbury/Busselton to Albany. A first order connection between Roy Hill and Mount Anderson was also observed which combined a Tellurometer traverse with first order triangulation based on Geodimeter measured baselines. It was perhaps during this work that the photograph at Figure 71, was taken. Corporate memory has it that the Geodimeter was not the success that the Lands Department had hoped. There is a record however, of the Geodimeter and Tellurometer set up side by side so as to measure the same line. Given the availability of the Tellurometer this event has to be late 1957-early 1958 and fits with the Western Australia Lands Department phasing out its use of the Geodimeter in 1958.

 

National Mapping also used its Geodimeter for the last time in March 1958, following a series of measurements for the Tasmanian Department of Lands and Survey.

The National Mapping Council in 1959, recommended that :

 

Geodimeters were best for measuring lines of length of 1 to 20 miles with an average accuracy of 2 parts in 1 000 000 (60 millimetres in 30 kilometres);

 

Tellurometers were best for measuring lines of length of 10 to 50 miles with an average accuracy of 5 to 10 parts in 1 000 000 (80 millimetres in 80 kilometres).

 

The following table was extracted from Keith Waller's 1955 article Field Use of the Geodimeter, to show the comparisons between the chained baselines and the Geodimeter measurements. As all these baselines were originally measured by RA Survey, they must get the credit for their excellent work. Hurren (1959) recorded that RA Survey also used their Geodimeter to measure the Jondaryan baseline.

 

 

 

Australian Triangulation Baselines Summary Table

 

BASELINES 1830s
REFERENCE	STATE	YEAR	APPARATUS	BASELINE NAME	LATITUDE	LONGITUDE	DIST (metres)	DIST (miles)	NOTES
1	NSW	1828	Unspecified	BOTANY BAY BASELINES	-34.00	151.21	761	0.5	Two baselines of 832 yards each at Botany Bay
2	NSW	1828	Two Deal Rods each of about 10 feet	LAKE GEORGE NORTH BASELINE	-35.00	149.40	1609	1.0	Reported to be 1 mile long
3	NSW	1831	Unspecified	LIVERPOOL PLAINS BASELINE	-31.60	150.50	4828	3.0	Reported to be 3 miles long
4	QLD	1839	10 feet Deal Rods X 3	DIXON IPSWICH	-27.81	152.65
				DIXON IPSWICH	-27.85	152.63	4797	3.0	Reported to be 3 miles long
5	QLD	1849	10 feet Deal Rods X 3	BURNETT JONDARYAN	-27.48	151.54
				BURNETT JONDARYAN	-27.51	151.53	3421	2.1	Reported to be 2 miles 10 chains (170 chains) long
BASELINES pre-1912
REFERENCE	STATE	YEAR	APPARATUS	BASELINE NAME	LATITUDE	LONGITUDE	DIST (metres)	DIST (miles)	NOTES
6	SA	1840	100 feet & 66 feet chains	ADELAIDE BASE CITY END	-34.92	138.59
				ADELAIDE BASE MASTERS HILL	-34.94	138.53	5324	3.3	Mean length stated as 17 462.2 feet (3¼ miles)
7	SA	c1850	Unspecified	BURRA BALD HILL BASE	-33.65	138.88
				BURRA MOUNT BRYAN BASE	-33.42	138.97	26845	16.7
8	SA	1857	66 feet/100 link chain & basenet	MOUNT SERLE ARCOONA BLUFF	-30.42	138.98			Reportedly 2 miles, expanded
				MOUNT SERLE MOUNT ROWE	-30.52	138.95	12150	7.6	to 7.55 miles by basenet
9	SA	1858	66 feet/100 link chain	HOOKINA CASTOR BASE	-31.79	138.27
				HOOKINA POLLUX BASE	-31.75	138.33	7068	4.4	Reportedly measured at 23 189.7 feet
10	NSW	1859	Unspecified	ALBURY BASELINE	-35.90	146.95	3168	0.6	Reportedly 48 chain at Ellerslie; today Elderslie (NSW1952)
11	SA	1859	66 feet/100 link chain	TERMINATION HILL BASE	-30.25	138.04			Reported as using an Ordinary Chain
				TWENTYMILE HILL BASE	-29.96	138.04	32266	20.0	measured 105 861.9 feet
12	SA	1859	66 feet/100 link chain	MT MARGARET BASE	-28.60	136.37			Reported as using an Ordinary Chain
				MT MARGARET BASE	-28.44	136.38	17807	11.1	measured 58 423.2 feet
13	VIC	1860	10 feet Iron Bar X 3	WERRIBEE BASE	-37.85	144.62
				WERRIBEE BASE	-37.89	144.70	7953	4.9	Reported length 26 091.826 feet
				WERRIBEE EXTN GREEN HILL	-37.80	144.54	17048	10.6	Reported total length of 55 931.65 feet
14	SA	1861	66 feet/100 link chain	HURD HILL BASE	-32.29	140.52
				HURD HILL BASE	-32.34	140.39	12942	8.0	Reportedly chained 8 miles 336 links (42 461.76 feet)
15	NT	1870	Unspecified	McMINNS BASELINE	-13.75	131.73	Unspecified	Unspecified
16	NSW	1873	10 feet Wooden Bar X 3	LAKE GEORGE BASE	-35.24	149.42
				LAKE GEORGE BASE	-35.17	149.47	8935	5.6	Reportedly 29 286 feet
17	NSW	1875	Steel Band	BULLENBUNG BASE	-35.21	146.92			South terminal is at Tollendool Hill
				BULLENBUNG BASE	-35.12	146.98	11454	7.1
18	NSW	1879	Steel Bands of 66, 100, 200 feet	NEWCASTLE BASELINE	-32.93	151.75	2200	1.4	Twynam reported upwards of 7 200 feet
19	NSW	1879	10 feet Wooden & Steel Bars X 3 each	RICHMOND BASE	-33.60	150.78
				RICHMOND BASE	-33.66	150.68	11274	7.0	Reportedly of some 7 miles
20	SA	1880	Deal Bars & Steel Rods	THALEPITTINNA CLAYPAN BASE	-27.57	138.55			Bars and rods both of 10 links
				THALEPITTINNA CLAYPAN BASE	-27.60	138.56	2776	1.7	Reportedly measured at 9 107.71 feet
21	QLD	1883	100 feet Steel Bands X 2	JONDARYAN MT MARIA BASE	-27.47	151.49			Reportedly accepted in 1883 as 37 029.7549575 feet
		1939	50 metre Invar Bands X4 & steel standards	JONDARYAN MT IRVING BASE	-27.51	151.59	11286	7.0	Resistance thermometry employed - 37 029.41157 feet
22	NT	1884	Unspecified	ROPER RIVER BASELINE	-15.00	133.80	Unspecified	Unspecified
23	WA	c1885	66 feet steel wire	PERTH BASELINE	-31.95	115.86	Unspecified	Unspecified
24	WA	c1885	66 feet steel wire	GERALDTON BASELINE	-29.00	114.90	Unspecified	Unspecified
25	WA	c1885	66 feet steel wire	GASCOYNE RIVER BASELINE	-25.10	115.76	Unspecified	Unspecified
26	WA	c1885	66 feet steel wire	GLOBE HILL BASELINE	-22.59	115.30	Unspecified	Unspecified
27	WA	c1885	66 feet steel wire	FITZROY RIVER BASELINE	-18.30	125.73	Unspecified	Unspecified
28	WA	1885	66 feet steel wire	WYNDHAM QUOIN HILL BASE	-15.32	128.21
				WYNDHAM EAST BASTION BASE	-15.44	128.16	14322	9.0
29	QLD	c1888	100 feet band & basenet	BRISBANE EILDON HILL BASE	-27.43	153.02			Reportedly 1 923.739 feet expanded
				BRISBANE MT PETRIE BASE	-27.53	153.13	15045	9.3	to about 9 miles 25 chains by basenet
30	WA	1899	Invar 500 link Band	LAKE CAREY BASELINE	-28.95	122.28	Unspecified	Unspecified
31	WA	1899	Invar 500 link Band	LAKE RAESIDE BASELINE	-29.40	121.94	Unspecified	Unspecified
32	WA	1904	Invar 500 link Band	KIMBERLEY BASELINE	-17.88	124.00	Unspecified	Unspecified	Three baselines in 1904, 1905 and 1907
33	NT	1906	Unspecified	VICTORIA RIVER BASELINE	-15.61	131.00	Unspecified	Unspecified
34	WA	1906	Invar 500 link Band	DE GREY BASELINE	-20.27	119.10	Unspecified	Unspecified
35	WA	1906	Invar 500 link Band	JENNABERRING BASELINE	-31.90	117.47	Unspecified	Unspecified
36	WA	1908	Invar 500 link Band	ROCKINGHAM BASELINE	-32.30	115.75	Unspecified	Unspecified
37	WA	c1911	Invar 500 link Band	IRWIN BASE	-29.27	115.26
		c1911		IRWIN BASE	-29.30	115.16	9752	6.1	Reportedly 48 500 links
BASELINES 1920s-1950s
REFERENCE	STATE	YEAR	APPARATUS	BASELINE NAME	LATITUDE	LONGITUDE	DIST (m)	DIST (miles)
38	QLD	1921	5 Chain Invar Band	IPSWICH BASE	-27.76	152.65
				IPSWICH BASE	-27.85	152.66	10621	6.6	Reportedly 52 797.391 links
39	VIC	1926	5 Chain Invar Band	CORA LYNN	-38.15	145.61	4949	3.1	Reportedly 16 236.067 feet
40	NSW	1927	24 metre Invar band x 4	BOURKE BASE	-30.30	146.10
				BOURKE BASE	-30.53	146.29	31554	19.6	Reportedly just over 19.6 miles
41	VIC	c1930	5 Chain Invar Band	MORWELL BASE	-38.25	146.45
				MORWELL BASE	-38.27	146.44	2726	1.7
42	SA	1934	5 Chain Invar Band	MILLICENT BASE	-37.33	140.67
				MILLICENT BASE	-37.40	140.68	7364	4.6
43	SA	1934	5 Chain Invar Band	TARLEE BASE	-34.30	138.80
				TARLEE BASE	-34.30	138.72	7623	4.7
44	NT	1937	Unspecified	RYAN WELL BASE	-22.64	133.40
				RYAN WELL BASE	-22.56	133.44	9710	6.0
45	NSW	1939	50 metre Invar Bands X4 & steel standards	SOMERTON BASE	-30.86	150.60
				SOMERTON BASE	-30.94	150.59	8605	5.3	Resistance thermometry employed - 28 239.17308 feet
46	VIC	1940	5 Chain Invar Band	BENAMBRA BASE	-36.93	147.70
				BENAMBRA BASE	-37.01	147.66	9510	5.9
47	SA	1941	5 Chain Invar Band	CARRIETON BASE	-32.33	138.60
				CARRIETON BASE	-32.35	138.53	6995	4.3
48	QLD	1942	300 feet Steel 5 Chain Invar Band	TOWNSVILLE NORTH	-19.21	146.76
				TOWNSVILLE SOUTH	-19.25	146.74	4900	3.0
49	QLD	1942	300 feet Steel 5 Chain Invar Band	GORDONVALE EAST	-17.08	145.81
				GORDONVALE WEST	-17.08	145.79	2130	1.3	Reportedly 7 000 feet
50	QLD	1942	300 feet Steel 5 Chain Invar Band	KAIRI (CAIRNS) BASE	-17.22	145.54
				KAIRI (CAIRNS) BASE	-17.20	145.54	2100	1.3	Reportedly of similar length to the Gordonvale baseline
51	NT	1942	300 feet Steel 5 Chain Invar Band	ADELAIDE RIVER BASE	-13.24	131.16
				ADELAIDE RIVER BASE	-13.20	131.15	4882	3.0
52	QLD	1942	300 feet Steel 5 Chain Invar Band	BOWEN BASE	-20.02	148.25
				BOWEN BASE	-20.04	148.23	2844	1.8
53	QLD	1942	300 feet Steel 5 Chain Invar Band	IRON RANGE NORTH BASE	-12.78	143.31
				IRON RANGE SOUTH BASE	-12.80	143.30	2445	1.5
				IRON RANGE EAST BASE	-12.80	143.32
				IRON RANGE WEST BASE	-12.78	143.30	2554	1.6
54	QLD	1942	300 feet Steel 5 Chain Invar Band	CAPE YORK BASE	-10.72	142.45
				CAPE YORK BASE	-10.74	142.44	1980	1.2
55	WA	1942	300 feet Steel 5 Chain Invar Band	GASCOYNE JUNCTION	-25.10	115.21
				GASCOYNE JUNCTION	-25.15	115.11	11812	7.3
56	QLD	1944	300 feet Steel 5 Chain Invar Band	COOKTOWN	-15.45	145.17
				COOKTOWN	-15.44	145.12	5433	3.4
57	WA	1944	300 feet Steel 5 Chain Invar Band	ROEBOURNE	-20.75	117.16
				ROEBOURNE	-20.80	117.16	5761	3.6
58	NSW	1945	Invar Band	CONDOBLIN BASELINE	-33.03	147.21
				CONDOBLIN BASELINE	-33.10	147.31	11371	7.1	Quoted as 7 miles
59	WA	1947	5 Chain Invar Band	NOONKANBAH NORTH BASE	-18.24	125.73
				NOONKANBAH SOUTH BASE	-18.26	125.66	7508	4.7
				NOONKANBAH EAST BASE	-18.30	125.73	6756	4.2
60	SA	1950	50 metre Invar Bands X4 & steel standards	KOOLYMILKA BASELINE	-30.95	136.41			Resistance thermometry employed
				KOOLYMILKA BASELINE	-30.85	136.43	11499	7.1	Reportedly 7 miles
61	NSW	1954	Never directly measured	BROKEN HILL BASE	-31.88	141.53
				BROKEN HILL BASE	-31.91	141.49	4892	3.0
62	NSW	1955	5 Chain Invar Band	MILDURA BASE	-34.10	142.22
				MILDURA BASE	-34.13	142.26	5210	3.2
63	WA	1957	Tellurometer	WYNDHAM BASE	-15.54	128.20
				WYNDHAM BASE	-15.55	128.25	5520	3.4

 

 

 

The Tellurometer : the end of triangulation

National Mapping now became focussed on extending the triangulation to first order standards, from the south east to the north and north west. From the vicinity of Carrieton, the triangulation network used some of the South Australian stations from their work in the late 1800s, to proceed north to Alice Springs. At the South Australian-Northern Territory border the triangulation branched due west to the vicinity of the Giles Meteorological Station. Enroute the heights of Ayers Rock (Uluru), The Olgas and Mount Woodroffe were incorporated. From Alice Springs the triangulation continued north past Aileron to around Wauchope and north west to around The Granites. Also, during this time, a network on the Eyre Peninsula of South Australia was observed, as well as a network from Broken Hill to the vicinity of Cobar. The Broken Hill-Cobar triangulation now connected the New South Wales, Bourke baseline with the South Australian, Carrieton baseline.

 

During the 1950s and early 1960s, New South Wales further developed their triangulation networks. Of note was their 1957-58, Condobolin baseline to Somerton baseline triangulation to first order standards. In addition, a second order triangulation adjacent and connected to this chain in the Tamworth-Coonabarabran region was also observed.

 

Triangulation also connected Tasmania to the mainland. After initial reconnaissance and marking of a network via Flinders island in 1949, Nat Map observed the triangulation in the summer of 1952-53. An independent connection between Tasmania and the mainland via King Island, was achieved in 1963. This connection however was able to use the Tellurometer to measure the necessary distances.

 

By the mid 1950s National Mapping had just about reached the last prominence before the vast northern and western deserts. The terrain now dictated that any triangulation would be by using many short lines and therefore many more baselines or more triangle sides would need to be measured with the Geodimeter.  In July 1957, however, the first Tellurometer was tested in Australia. Using microwaves to measure distance, the Tellurometer was lighter, more portable, less complex to use and was able to measure longer distances than the Geodimeter. With appropriate operating procedures distances accurate to first order standards could now be measured night or day. It was now possible to make a theodolite and Tellurometer traverse from point to point. If these traverses closed on themselves or other first order work the equivalent of triangulation was achieved with far less effort.

 

By the early 1960s, some 40 Tellurometer sets were in use by Nat Map, RA Survey and the State mapping agencies; the days of triangulation were past. For completeness in 1957 the RA Survey acquired the Geodimeter, but for the same reasons found by Nat Map it was quickly replaced by the Tellurometer. All the survey and mapping agencies now used the theodolite and Tellurometer traverse technique for new work, to strengthen existing triangulation or measure lines of existing triangulation thus creating a traverse of similar or higher order.

 

 

 

Australian Baselines for Space Triangulation and Geodesy

From 1967 to 1970, National Mapping refined existing triangulation and traverse surveys to generate two continental baselines. Please refer to Figure 72 below. The east-west Perth, Western Australia-Culgoora, New South Wales baseline comprised 162 surveyed segments with a final computed length of 3 692 kilometres and the north-south Culgoora, New South Wales-Thursday Island, Queensland baseline comprised 102 survey segments with a final computed length of 2 910 kilometres. Similar baselines were established in North America, Europe and Africa.

 

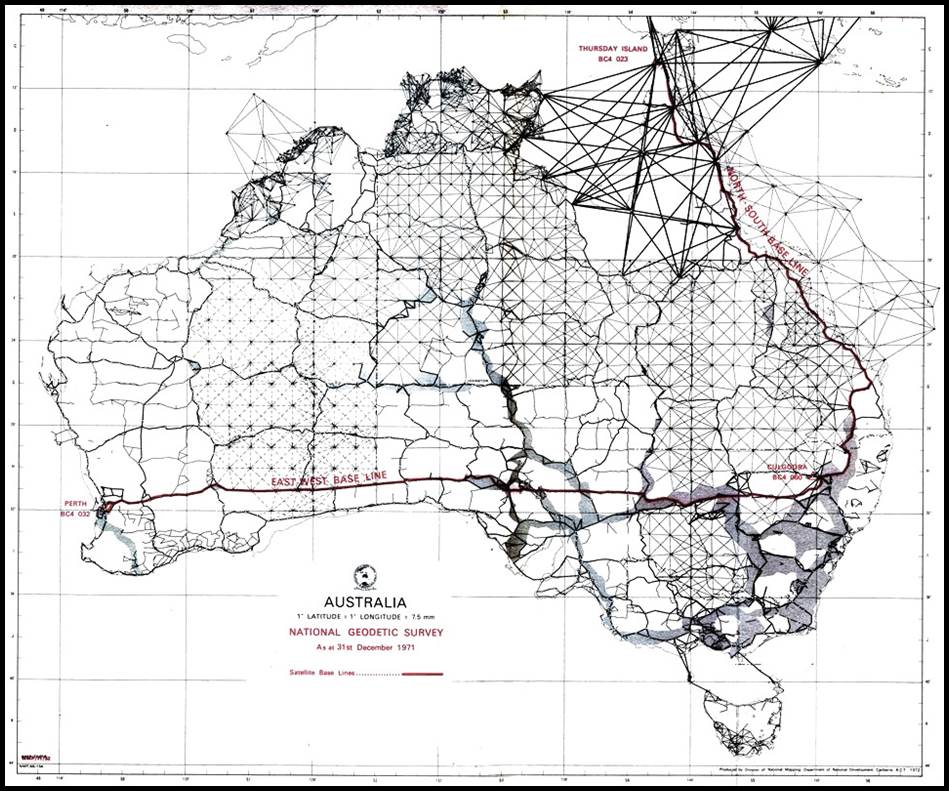
Figure 72 : Map showing survey routes for the PAGEOS north-south and east-west baselines.

 

These baselines were part of a global cooperation Weltnetz der Satellitentriangulation (Worldwide Satellite Triangulation Network). At the ends of these baselines in conjunction with over 40 stations worldwide the orbiting PAGEOS (Passive Geodetic Earth Orbiting Satellite) was simultaneously photographed against the star background from respective stations. From these photographs a network of directions could be established to determine, except for scale, the relative locations of the ground stations. From this stellar triangulation, the relative locations of ground stations 3 000 to 5 000 kilometres apart were obtained. Just like with terrestrial triangulation, to provide and maintain scale throughout this stellar network, the highly precise continental baseline distances were required.

 

Finished in 1974, the PAGEOS network connected stations previously on seven different geodetic ellipsoids (International, Clarke 1866 and 1880, South American, Bessel, Everest, and Australian National) with an accuracy of better than 20 metres. A best fitting global ellipsoid was defined from these data with an equatorial radius of 6,378,130 metres. In 1984 when the GPS ellipsoid was determined at 6,378,137 metres the 1974 work was shown to produce a value to better than 1 part per million.

 

 

 

Australian Triangulation Baseline Legacy

Although electronic distance measuring equipment eliminated the need for triangulation, the baselines themselves continued to provide a valuable facility. As already seen Carrieton, Benambra, Somerton and Jondaryan baselines served to validate the accuracy of the NASM model Geodimeters. From then on, these baselines were used again and again, right up and into the 1970s, to test that the calibration of the electronic distance measuring equipment in use, was delivering their specified accuracy. Ford (1979) recorded that from mid November to mid December 1967 and also in February 1968 extensive testing of all Tellurometer Models, MRA-1, MRA-2, MRA-4, 101 and the Wild Distomat were carried out at Benambra. Further, over a two week period in August 1968, the Somerton baseline was used for MRA-4 Tellurometer testing.

 

Records showed that National Mapping measured the Benambra baseline in 1969, the Carrieton baseline in 1971 and the Somerton baseline in 1971 (late October Murphy (2020) recalled with the Geodimeter measurement within a few millimetres of the accepted length) and 1972, with AGA Model 8 (Laser) Geodimeters, As the originally received Geodimeters failed acceptance testing the two replacement instruments were received in May and September 1969, respectively. Thus the 1969 measurement at Benambra was probably to evaluate the newly received Model 8 Geodimeter(s), the other three measurements were undertaken whilst work on the High Precision traverse was being undertaken nearby, during the early 1970s. (The High Precision geodetic traverse extended from the Johnston Origin in the southern Northern Territory generally south to Mount Gambier in South Australia, then along coastal Victoria and north through New South Wales to connect with the Culgoora Ballistic Camera (BC4 Site 060) station about 25 kilometres north west of Narrabri. As already shown in Figure 72 above Culgoora, was the terminal for both the east-west and north-south continental baselines. The High Precision survey was undertaken using AGA Model 8 (Laser) Geodimeters for distance measurement and Wild T3 theodolites for angular and astronomical observations.)

 

Respected geodetic surveyor Howard Angas (Bill) Johnson (1907-1990), saw the end of geodetic triangulation in Australia and its replacement by traversing with electronic distance measuring equipment, namely the Geodimeter and later Tellurometer. In RA Survey (1936-1954), Johnson rose to the rank Lieutenant Colonel and Chief Instructor at the Army School of Military Survey. In National Mapping (1954-c1971) he was the Supervising Surveyor Geodetic Branch, until standing down in 1968 and taking on other duties.

 

In his 1962 paper, First Order Angular Control, Johnson reviewed his experience with both survey techniques. Irrespective of the survey technique used, however, Johnson steadfastly advocated that a geodetic survey was only as good as its marking and its records and that a more remote and difficult to reach station should be marked and observed with even greater care. Johnson stated :

 

It has been our [National Mapping] policy, wherever early triangulation was established, to adopt such marks exactly, and in this matter the marking of the original trigonometrical work of the old South Australian Survey Department is outstanding in Australia and deserves mention. Most of their cairns, particularly through the Flinders and Gawler Ranges are magnificent, craftsman built monuments 8 to 10 feet high, in some cases 100 years old and in many instances without a stone dislodged. On sandhills and gibber rises, lacking in larger stones, massive, pyramidal mulga cages were erected, and many of these still stand and some have been used by our parties. In very flat country, near Mataranka to Newcastle Waters, and across the Nullarbor Plain, 20' and 30' galvanized windmill stands have been erected on concrete emplacements [by National Mapping], and after use as instrument stands, have been left as future marks.

 

In 1939 the use by the Royal Australian Survey Corps of the electrical resistance method of standardising baseline bands [later meant that] these baselines measured by this method were to be invaluable in proving the accuracy of the Geodimeter and the Tellurometer…these were comparatively short lines of about 5 to 7 miles on very carefully selected ground. From 1954 to 1957 the Division of National Mapping carried out normal geodetic triangulation methods over good trigonometrical terrain, as encountered in the Flinders, Gawler, Macdonnell and Musgrave Ranges, fading off into low lying areas where the rays skimmed to and from low residuals and sandridges. In 1954 the Geodimeter did away with the need for costly and elaborate baseline measurement and extension, and began to prove in some instances how quickly scale fell away in triangulation chains. 1957 saw the arrival of the Tellurometer and the beginning of the wholesale onslaught by Commonwealth and State mapping authorities on the geodetic scheme which now covers Australia. Until the middle of 1957, in Division of National Mapping, normal triangulation methods were used on geodetic work.

 

 

 

 

Acknowledgements

The valuable assistance and contributions of Kaye Nardella, Senior Curator, and Bill Kitson, former Curator, Museum of Lands, Mapping and Surveying, Land and Spatial Information, Department of Natural Resources, Mines and Energy, for the supply of rare Queensland related documents and information is greatly appreciated.

 

My thanks, also to the following, for their contribution :

 

Tony Castelli, Geodesist–Survey Services, Location Data Services, Landgate, Western Australia, for supplying information on the use of the Geodimeter in Western Australia by the Western Australia Lands Department;

 

Ken Green, Co-ordinator of The Pathfinders, Seniors Group of Surveyors, Institution of Surveyors NSW, especially for his work in determining the details of the Condobolin baseline. Ken’s information enabled information on other New South Wales baselines to also be extracted; and

 

Former Natmappers, Laurie McLean, Bill Stuchbery and Brian Murphy for wide ranging research information and support.

 

 

 

 

Sources

Anonymous (1857), Discoveries in the North, Adelaide Times, Friday 10 July 1857, Page 2, accessed at : https://trove.nla.gov.au/newspaper/article/207122525?searchTerm=triangulation%20base%20line&searchLimits=dateFrom=1850-01-01|||dateTo=1900-12-31|||l-advstate=South+Australia|||l-advcategory=Article

 

Anonymous (1860), Bespoke from Ms. Goyder [regarding her husband’s survey activities in South Australia], South Australian Register, Wednesday 4 April 1860, Page 3, accessed at :

https://trove.nla.gov.au/newspaper/article/49892272?searchTerm=triangulation%20base%20line&searchLimits=dateFrom=1850-01-01|||dateTo=1900-12-31|||l-advstate=South+Australia|||l-advcategory=Article#

 

Anonymous (1865), Geodetic Survey, The Sydney Morning Herald, Thursday 28 December 1865, Page 2, accessed at : https://trove.nla.gov.au/newspaper/article/31126250?searchTerm=geodetic%20survey&searchLimits=l-format=Article|||l-title=35|||l-decade=186

 

Anonymous (1869), Base Line for the Triangulation of New South Wales, The Sydney Morning Herald, Monday 11 October 1869, Page 2, accessed at : https://trove.nla.gov.au/newspaper/article/13193293?searchTerm=base%20line&searchLimits=l-title=35|||l-category=Article|||l-decade=186

 

Anonymous (1873), Geodetic Survey of Victoria, Age, Saturday 5 July 1873, Page 7, accessed at : https://trove.nla.gov.au/newspaper/article/202518786?searchTerm=trigonometrical%20base%20line&searchLimits=dateFrom=1850-01-01|||dateTo=1900-12-31|||l-advcategory=Article|||l-state=Victoria

 

Anonymous (1874), The Base Line at Lake George, Australian Town and Country Journal, Saturday 21 March 1874, Page 14, accessed at :

https://trove.nla.gov.au/newspaper/article/70473274?searchTerm=lake%20george%20base%20line&searchLimits=exactPhrase|||anyWords|||notWords|||requestHandler|||dateFrom=1840-01-01|||dateTo=1900-12-31|||l-advstate=New+South+Wales|||l-advcategory=Article|||l-word=*ignore*%7C*ignore*|||l-illustrated=*ignore*%7C*ignore*|||sortby

 

Anonymous (1880), Triangulation of the Colony, Goulburn Herald and Chronicle, Wednesday 18 August 1880, Page 4, accessed at : https://trove.nla.gov.au/newspaper/article/101449062?searchTerm=TRIANGULATION%20COLONY&searchLimits=exactPhrase|||anyWords|||notWords|||requestHandler|||dateFrom=1880-01-01|||dateTo=1880-12-31|||l-advstate=New+South+Wales|||l-advcategory=Article|||l-word=*ignore*%7C*ignore*|||l-illustrated=*ignore*%7C*ignore*|||sortby#

 

Anonymous (1885), Report on the Survey of the Kimberley District, Saturday 5 December 1885, Page 5, accessed at : https://trove.nla.gov.au/newspaper/article/3004699?searchTerm=trigonometrical%20base%20line&searchLimits=dateFrom=1850-01-01|||dateTo=1900-12-31|||l-advcategory=Article|||l-state=Western+Australia

 

Anonymous (1891), Survey of Moreton Bay, Queenslander, Saturday 8 August 1891, Page 278, accessed at : https://trove.nla.gov.au/newspaper/article/20295211?searchTerm=triangulation%20base%20line&searchLimits=exactPhrase|||anyWords|||notWords|||requestHandler|||dateFrom=1850-01-01|||dateTo=1900-12-31|||l-advstate=Queensland|||l-advcategory=Article|||sortby

 

Anonymous (1894), Trigonometrlcal Survey : Work in Queensland, Telegraph, Friday 22 June 1894, Page 7, accessed at : https://trove.nla.gov.au/newspaper/article/173163740?searchTerm=triangulation%20base%20line&searchLimits=exactPhrase|||anyWords|||notWords|||requestHandler|||dateFrom=1850-01-01|||dateTo=1900-12-31|||l-advstate=Queensland|||l-advcategory=Article|||sortby

 

Anonymous (1906), Obituary (William Turton), Australasian, Saturday 23 June 1906, page 39, accessed at : https://trove.nla.gov.au/newspaper/article/139185831?searchTerm=turton&searchLimits=exactPhrase|||anyWords|||notWords|||requestHandler|||dateFrom=1906-01-01|||dateTo=1906-12-31|||l-advstate=Victoria|||sortby|||l-title=460

 

Anonymous (1911), Lands and Surveys Department : Surveyor General's Annual Report :  Year Ending June 30, 1911, West Australian, Friday 15 December 1911, Page 8, accessed at : https://trove.nla.gov.au/newspaper/article/23859375?searchTerm=jennaberring%20base&searchLimits=dateFrom=1850-01-01|||dateTo=1950-12-31|||l-advstate=Western+Australia|||l-advcategory=Article

 

Anonymous (1945), Trigonometrical Survey : Interesting Interview :  Wonderful Instruments, Lachlander and Condobolin and Western Districts Recorder, Thursday 13 September 1945, Page 1, accessed at :

https://trove.nla.gov.au/newspaper/article/214476096?searchTerm=Trigonometrical%20Survey%20-%20Interesting%20Interview%20-%20Wonderful%20Instruments&searchLimits=l-state=New+South+Wales|||l-format=Article|||sortby=dateAsc|||l-title=1153

 

Andrews, AEJ (1994), Major Mitchell’s Map : Map of the Colony of New South Wales; explanation accompanying this special edition, accessed at: http://nla.gov.au/nla.obj-232180396/view

 

Benwell, George L (1987), The Victorian Geodetic Base­line, The Australian Surveyor, Vol.33, No.8, pp. 751-775.

 

Benwell, George L (1991), Tracking Turton in Gippsland, The Australian Surveyor, Vol.36, No.3, pp.227-239.

 

Brock, John (2006), A Tale of Two Maps - NSW in the 1830s by Mitchell and Dixon ; Perfection, Probity and Piracy!, 400 Years of Mapping Australia Conference, Paper 5, accessed at : http://xnatmap.org/adnm/conf_06_11/c06/aPaper%2005.pdf

 

Butterfield, Arthur D (1906), A History of the Determination of the Figure of the Earth from Arc Measurements, Davis Press, accessed at : https://www.google.com/search?q=26+determinations+of+figure+of+earth&client=firefox-b-d&ei=4WCEXJ-3L4-evQTAs6KoCg&start=10&sa=N&ved=0ahUKEwjfq7T6rvbgAhUPT48KHcCZCKUQ8NMDCKoB&biw=1421&bih=1028

 

Capon, Leigh Beresford (1989), The Search for Burnett’s Gowrie, in technical papers of the 31st Australian Survey Congress and 15th National Surveying Conference, Hobart, Tasmania, 1-7 April 1989.

 

Castelli, Tony (2019), Personal communications.

 

Chappel, Keith Lytton (1966), Surveying for Land Settlement in Victoria 1836-1960, Department of Lands and Surveys Victoria.

 

Clarke, Alexander Ross (1866), Comparison of Standards of Length : England, France, Belgium, Prussia, Russia, India, Australia, Eyre and Spottiswoode, London, accessed at: https://pahar.in/wpfb-file/1866-comparison-of-standards-of-length-of-england-france-belgium-prussia-russia-india-australia-by-clarke-s-pdf/

 

Commonwealth Government Handbook (1914), British Association for the Advancement of Science, (G.H. Knibbs, Ed.), Eighty-fourth Meeting, Australia, August 1914, AJ. Mullett, Government Printer. Melbourne.

 

Conference of Surveyors-General (1912), Conference of the Director of Commonwealth Lands and Surveys, the Surveyor-General and the Government Astronomer of New Zealand, and the Surveyors-General of the States of the Commonwealth of Australia : Melbourne, 20th to 25th May, 1912, Melbourne, Albert J. Mullett, Acting Government Printer, C.6832.

 

Coulthard-Clark, Christopher David (2000), Australia’s Military Map-Makers: The Royal Australian Survey Corps 1915-96, Oxford University Press, Melbourne, ISBN 0 19 551343 6.

 

Cumpston, JHL (1954), Thomas Mitchell: Surveyor General and Explorer, courtesy Project Gutenberg accessed at: http://gutenberg.net.au/ebooks07/0700531h.html

 

Denison, William Thomas (1857), Land Surveying, The Empire (a former Sydney newspaper), Wednesday 2 September 1857, Page 3, accessed at: http://xnatmap.org/ahist/docs/Denison_survey.htm

 

Ellery, Robert Lewis John (1888), The Survey of Victoria, Victoria and its Metropolis Past and Present, The Colony and its People in 1888, McCarron, Bird & Co., 1888, Vol. II, Chapter 1, pp.1-8.

 

Ellery, Robert Lewis John (1891), Brief Sketch of the Geodetic Survey of Victoria, Victorian Institute of Surveyors, pp.1-8, accessed at : https://nla.gov.au/nla.obj-394136057/view?partId=nla.obj-394136307

 

FitzGerald, Lawrence (1933), The Co-Ordination of the Trigonometrical Surveys of Queensland, New South Wales, Victoria and South Australia, The Australian Surveyor, March 1934, pp.22-31.

 

FitzGerald, Lawrence (1939), Report on the Measurement of the Jondaryan and Somerton Base Lines, published by Army Headquarters, Melbourne, C1015, Government Printer, Melbourne, 1939.

 

FitzGerald, Lawrence (1948), Mapping a Continent, Walkabout, Australian Geographical Magazine, Journal of the Australian Geographical Society, Vol.14, No.10, 1 August 1948, pp.9-15, accessed at : https://nla.gov.au/nla.obj-739085301.

 

FitzGerald, Lawrence (1980), Lebanon to Labuan: a story of mapping by the Australian Survey Corps World War II (1939-1945), JG Holmes Pty Ltd, Melbourne, June 1980.

 

Ford, Reginald Arthur (1979) The Division of National Mapping’s part in the Geodetic Survey of Australia, The Australian Surveyor, Vol.29, No.6, pp.375-427; Vol.29, No.7, pp.465-536; Vol.29, No.8, pp.581-638, accessed at : http://xnatmap.org/adnm/ops/prog/rafgeosvy/index.htm

 

Foster, William Charles (1985), Sir Thomas Livingston [sic] Mitchell and his World 1792-1855, The Institution of Surveyors NSW Inc., Sydney 1985.                   

 

Furber, Thomas Frederick (1898), The Trigonometrical Survey of New South Wales : With mention of Similar Surveys in the other Australian Colonies, Australasian Association for the Advancement of Science, 7th Meeting, Sydney, pp.176-229, Government Printer Sydney.

 

Government of Victoria (1861), Supplement to the Victoria Government Gazette of Friday, March 1, 1861, No.32, Monday, March 4, 1861, pp.472, accessed at : http://gazette.slv.vic.gov.au/images/1861/V/general/32-a.pdf

 

Green, Ken (2019), Personal communications.

 

Hurren, Albert Francis (1959), The Geodetic Survey of Australia, an article published in Cartography, Vol.3, No.1, March 1959, pp.38-48; accessed at: http://www.xnatmap.org/adnm/ops/prog/hurren_geod.pdf

 

Johnson, Howard Angas (1962), First Order Angular Control, 6th Australian Survey Congress, Adelaide, accessed at : http://www.xnatmap.org/adnm/ops/specs/foac.htm

 

Jones, A R (1952), Lake George History, Goulburn Evening Post Newspaper, Friday 26 September 1952, Page 2, accessed at: https://trove.nla.gov.au/newspaper/article/99817686

 

Lambert, Bruce Philip, (1956), The Geodimeter and its Uses, The Australian Surveyor, Vol.16, No.4, pp.213-229, accessed at : http://xnatmap.org/adnm/docs/bpl/bpl%20geodimeter56.pdf

 

Lines, John Dunstan (1992), Australia on Paper – The Story of Australian Mapping, Fortune Publications, Box Hill.

 

Lines, John Dunstan (1999), Maps in All Seasons: A Concise History of the 2/1st Corps Field Survey Company RAE and 2/1st Aust. Army Topographical Survey Company 1940-1945, 2/1st Survey Association, Beaumaris, Victoria. Personal manuscript copy here.

 

Macdonald, Donald (1989), Brigadier Lawrence FitzGerald, OBE, National Bulletin of Survey Corps Associations, No.23, November 1989, accessed at :  http://www.rasurvey.org/actindex.html

 

Mansfield, Ralph (1833), On the Trigonometrical Survey of New South Wales, The New South Wales Magazine, Vol.1, No.1, pp.46-52 (August to December, 1833), Ann Howe, Sydney, accessed at : https://nla.gov.au/nla.obj-765171557/view?partId=nla.obj-765188059#page/n65/mode/1up

 

McLean, John Baynard (1967), A Short History of the Trigonometrical Survey of New South Wales, The Australian Surveyor, June, pp.135-143.

 

McLean, Lawrence William (2019), George Robert Lindsay Rimington (1908-1992), accessed at : http://xnatmap.org/adnm/people/aabout/Rimington/GRL%20Rimington.htm

 

McLean, Lawrence William (2019), Personal communications.

 

Menzies, Trevor (2011), Topographic Mapping in Australia 1910-1945, 100 Years of National Topographic Mapping Conference, Canberra 2011, Paper 3 on CD-ROM.

 

Moyal, Ann (2017), Surveyors : Mapping the Distance, Early Surveying in Australia, Australian Dictionary of Biography, accessed at : http://adb.anu.edu.au/essay/22

 

Mitchell, Thomas Livingstone (1853), Trigonometrical Survey of Port Jackson : commenced as a military survey by order of General Darling and continued as civil duties permitted or required, T&W Boone, London, accessed at : https://nla.gov.au:443/tarkine/nla.obj-231443454

 

Murphy, Brian Anthony John (2020), Personal communications.

 

National Mapping Council of Australia (1953), Standard Specifications for Horizontal and Vertical Control, National Mapping Office, NMO/53/11.2.

 

New South Wales State Government (2019), Land Registry Services : Parish and Historical Maps, accessed at : https://www.nswlrs.com.au/

 

Harris, Charles Hope (1880 and 1887), South Australian Field Service Handbook for Government Surveyors, compiled by the South Australian Survey Department under the direction of the Surveyor General.

 

Penry, Jerry (2019), Eimbeck’s Duplex Bars, The American Surveyor, accessed at : https://amerisurv.com/2019/03/09/eimbecks-duplex-bars/

 

Raisbeck, John James (1937), A Short History of the Military Survey of Australia 1907-36, The Australian Surveyor, September 1937, pp.334-337.

 

Twynam, Edward Twynam (1879), District surveyor Twynam to the Surveyor General transmitting memorandum of measurement of baseline at Newcastle with field notes, etc, unpublished, courtesy State Library of New South Wales accessed at: http://digital.sl.nsw.gov.au/delivery/DeliveryManagerServlet?embedded=true&toolbar=false&dps_pid=IE15722182

 

Vance, Thomas Alexander (1926), Triangulation, The Queensland Surveyor, Vol.8, No.2, pp.26-37.

 

Vance, Thomas Alexander (1938), The Present Methods of the Australian Survey Corps, The Australian Surveyor, March 1938, pp.54-64.

 

Waller, Charles Keith (1956), Field Use of the Geodimeter, Cartography, Vol.1, No.3, March 1956, pp.125-130, accessed at : http://xnatmap.org/adnm/docs/2013/aganasm/geodimeter%20reprint%20waller.pdf

  

Ward, John M (1969), Cowper, Sir Charles (1807–1875)', Australian Dictionary of Biography, National Centre of Biography, Australian National University, accessed at: http://adb.anu.edu.au/biography/cowper-sir-charles-3275/text4967

 

 

 

 

 

 

 

 

 

 

Annexure A

 

 

Base Line for the Triangulation of New South Wales

The Sydney Morning Herald, Monday 11 October 1869, Page 2

https://trove.nla.gov.au/newspaper/article/13193293?searchTerm=base%20line&searchLimits=l-title=35|||l-category=Article|||l-decade=186

 

The Government Astronomer

to the Principal Under Secretary

 

Sir, I have the honour to forward, for the information of the Honourable the Colonial Secretary, a progress report of the measurement of the baseline at Lake George for the triangulation of New South Wales.

 

1. In the Estimates for 1867 the Parliament voted £1090 for the measurement of the baseline for triangulation, and a further grant of £500 made in 1868

 

2. My first official instructions from your department to act in this matter were dated 16th January, 1867 and in accordance with these instructions I placed myself in communication with the then Surveyor-General, and the result of a conference between that gentleman, his deputy (now Surveyor General), and myself, will be shown in the copy of an appended minute agreed to by us on that occasion.

 

3. The results of inquiries made by district surveyors in different parts of the colony fully bore out my predilections in favour of Lake George being the best site for a baseline, and in July, 1867, Mr Adams and I met Mr District surveyor Twynam at the Lake, and after a careful examination, unanimously agreed that no better site could be conveniently selected.

 

4. Previous to this, I had written to the Astronomer Royal for England, to obtain for the New South Wales Government the loan of two very valuable and useful instruments which had been previously employed in similar operations. With Professor Airy's usual kind readiness to forward any useful scientific work, this application was acceded to I regret to say that these instruments were submerged when the ship John Duthie was scuttled in Port Jackson, and they had, at a considerable expense to be thoroughly cleaned and set in order by Mr Tornaghi, the optician, but I do not believe that there has been any permanent damage to them.

 

5. In March, 1867, I proceeded to Melbourne, for the purpose of examining the mode of carrying on the Trigonometrical Surveying Victoria, and likewise to negotiate for the loan of some apparatus, which was readily granted. At the time I was fortunate enough in recovering some well-seasoned pine bars belonging to the Government of New South Wales, and which appear to have been sent out some thirty years ago to the Government of Tasmania, and afterwards, through some mistake, deposited at the Lands Office, in Melbourne.

 

6. I may observe that I have long felt convinced that well-seasoned pine bars, with such arrangements as I have adopted for determining accurately the distance between each pair, are quite, if not more reliable than the very complicated compensation bars, which would have been an enormous expense, and required a much larger staff to work them than I have at my disposal; and this opinion is sustained by those of highly scientific and practical men. I believe that the hygrometrical and thermal changes will be almost inappreciable; but as a full account of the modus operandi and the results will be furnished in my final report, I presume that I need not enter further into details on the present occasion.

 

7. The remainder of 1867 and early part of 1868 was employed in making the preliminary arrangements, and mounting the ten-foot standard bar of the colony, which had been placed in my charge at the Observatory. Considerable time and expense was incurred in getting things up to the lake, so that it was not until nearly the end of May, 1868, that systematic operations were commenced.

 

8. The first work to be performed was the selection of the actual line, and in doing so it was necessary to keep it:-

 

(1) As level as possible

 

(2) Sufficiently removed from the swampy margin of the Lake.

 

(3) To cross two creeks at the narrowest points consistent with the other conditions so as to diminish as much as possible the expenditure of time and money in building the necessary bridges.

 

(4) It was necessary to clear the whole line of trees, so as to afford an uninterrupted view from end to end, and allow free passage for the bars and tents, also, to make extensive clearings, so as to obtain a view to the primary stations from the ends of the line.

 

All this has been satisfactorily effected.

 

9. At the commencement of operations, my force consisted of a carpenter cook and hutkeeper, and two general workmen. It soon, however, became evident that this was quite insufficient for the purpose, so that in August last I had to obtain the assistance of Mr Frank Russell to take charge of my camp, and carry out my instructions during my occasional and necessary absences. I had also to obtain the assistance of two day labourers and a boy, especially to assist in felling the heavy timber on the line and hills.

 

10. The length of the baseline is about 5 miles 64 chains and 72 links; the ends are not liable to inundation, and the line itself is indicated by five nearly equidistant solid stone pillars, resting about 3½ feet beneath the surface on granite foundations - having let into the upper surface a solid brass plug with a fine platinum dot inserted -this again protected by a brass plate screwed over it and again by a massive stone cap over the whole. These marks afford a lasting record of the operations, and will, when the final measurement is completed, be still further protected by stone structures, and I hope a moderate space around them reserved to the Crown. Doubtless these pillars and the expenses attending them have cost a great deal, but I think their value is quite commensurate with the outlay. In measuring a baseline, it is of the greatest importance that in future generations someone should be able to verify it; yet this is rarely possible. I may instance La Caille’s baseline at the Cape of Good Hope – a fine line, but not to be identified for want of permanent records. Sir Thomas Mitchell’s small baseline on the Botany Sands; also, his measured check line somewhere near Lake George. Now if any one, or even two of these pillars should at some future time be lost, the remainder known to have the platinum dots in a straight line, as nearly as science can bring them, and with the records of the entire work to refer to, would be quite sufficient to enable future surveyors to verify the work now in progress.

 

11. The next work was the selection of primary stations; and here I may observe that the necessary conditions are:-

 

1. That the triangles connecting them with the extremities of the baseline should be as nearly as possible equilateral.

 

2. That both ends of the baseline should be visible from each of the primary stations.

 

3. That the primary stations should command good secondary stations.

 

There was no difficulty about the one on the eastern side of the line, as the present Surveyor General, Mr District Surveyor Twynam, and myself, were unanimously of opinion that the one selected could not be surpassed, but I had great difficulties to contend with in finding a suitable primary station on the western side of the Lake. Several weeks were spent in examining the mountain ranges, and clearing intermediate hills, before I could select one answering the required conditions. Happily, I succeeded in obtaining a station nearly equal to the one on the east of the line.

 

12. I considered it important that on each of these hills should be erected a substantial stone column, about 15 feet high, to serve not only as permanent marks, but also as being of great value in measuring the primary and secondary triangles. One of these is completed, and the other will be finished shortly. A scaffold surrounds the pillar, and on the top is formed a convenient place for observing. The whole is surmounted by a white cone, which forms a well-defined object, visible at a very considerable distance.

 

13. I have dwelt at some length upon these primary stations, because owing to the heavy and unforeseen expense incurred over them, especially in the extensive clearing of trees, the whole of the vote for baseline measurement is exhausted, and it will be necessary to obtain a fresh supply in order to complete the work; this with favourable weather, I trust to do within three months. It would probably have been finished now, but for the time I was obliged to devote to the boundary between New South Wales and South Australia; but even as it is, with the drawbacks there have been, I am satisfied the time occupied will not be found excessive.

 

14. On the Estimates for the present year there is a vote to the Lands Department of £500 for commencement of triangulation; and I would respectfully urge that the Minister for Lands should be moved to sanction the application of such portion of this vote as may be required to enable me to complete the work I have undertaken. I have also to request that I may be empowered to draw from the Treasury, as hitherto, an advance, from time to time, of a sum not exceeding £50, to enable me to pay current expenses - vouchers in adjustment of each being forwarded as usual.

 

I have, &c,

George R. Smalley

Government Astronomer for New South Wales

4 June 1869

 

 

 

 

 

Annexure B

 

The Resistance Thermometry Technique

 

Resistance thermometry was a technique described by Professor Kerr Grant in 1940 (Grant, 1940). Developed by Grant, following a request by RA Survey, the usual measurement of air temperature with mercury thermometers to determine the change in length of the metallic measuring band was replaced by obtaining the electrical resistance of the band as the precise measure of its temperature, and hence of its change in length.

 

Thomas Alexander Vance (1882-1959) served in the Australian Survey Corps from July 1915 to November 1942. He was the officer commanding the Australian Survey Corps from 1936 to 1940. In 1935, then Major Vance now resident in Adelaide, had taken part in the measuring of the Millicent triangulation baseline along with then Lieutenant Lawrence FitzGerald (1903-1988).

 

The Millicent baseline had been measured in 1934 using Invar bands of 5 chains, standardised against the 66 feet floor standard of the New South Wales Lands Department. During the work, large differences in temperatures between the forward and back repeat measurements were observed with subsequent differences in sectional measurements being recorded. Doubts thus arose about the accuracy of the New South Wales standard for first order comparisons, and the extent to which the bands had reacted to the temperature changes. This concern prompted Vance to approach Kerr Grant (1878–1967, later Sir), Professor of Physics at the University of Adelaide, seeking a more accurate, practical method of determining the temperature of the metallic band at the time of measurement.

 

Invar is a nickel-steel alloy invented by Swiss physicist and metrologist Charles Édouard Guillaume in 1896. It was named Invar for its Invariability under extremes of heat or cold; its coefficient of expansion is 15 times less than that of steel. Nevertheless, over time Invar’s coefficient of expansion and its dimensions may change with time or when it is subjected to one or more cycles of heating and cooling to its initial temperature, even though the change in temperature is small.

 

Grant first determined the temperature coefficient of the electrical resistance of the Invar bands by raising the temperature of the bands and measuring the corresponding changes in their length. Simplistically, as the temperature of a material increases so does its resistance. The band’s temperatures were raised by passing through them varying amounts of electrical current. The results of Grant’s tests confirmed that an erroneous value for the thermal coefficient of expansion was being used for the Invar bands and when Grant’s value was then applied to the Millicent baseline measurements, the previous anomalies were resolved.

 

Vance was put in touch with SW Attwell at the National Physical Laboratories (NPL) at Teddington in England. Attwell had previously performed some similar experimental work in 1923/24, and was requested to test four 50 metre steel bands which, when coupled to a Kelvin Resistance Bridge, permitted the temperature of the bands to be determined in terms of their electrical resistance to within 0.1° Fahrenheit. This level of accuracy was a considerable and significant advance on then instrumental capabilities of mercurial thermometers. Accuracy to better than one part in a million was obtained, and the exact relationship between the length of the steel band and its resistance was determined once and for all. This method, however, was not by itself applicable for determinations of coefficients of thermal expansion. Standardisation of the steel bands thus permitted the steel measuring bands to be used in the field to establish an accurate standard against which the conventional Invar bands could be easily compared before and after daily usage. (Around 1950, the National Physical Laboratories repeated Attwell’s work, with minor electrical and mechanical upgrades and modifications. The conclusion was that in the intervening 25 years the steel bands standardised by Attwell had not changed in length by more than 2 parts per million (Clark and Johnson, 1951).)

 

The electrical aspects of the development were undertaken by Michael IG Iliffe, a physicist who specialized in electricity and magnetism under Grant at the University. Lieutenant FitzGerald handled the surveying requirements and design. Iliffe recalled the first experiments being conducted in a length of roof guttering to act as a temperature bath! Iliffe and FitzGerald completed their designs for the electrical resistance and survey components respectively. These were manufactured with some advice from, and under the supervision of, the National Physical Laboratories, with the final working equipment available to the RA Survey late in 1938.

 

 

A resistance Bridge (a form of Kelvin Double Bridge capable of measuring electrical resistances from 5 to 15 ohms to an accuracy of 0.001 ohms and powered by a battery; see photograph after Lawrence (1939) above and circuitry in Clark and Johnson (1951)) was designed and built for use in the field. Further, on Attwell’s advice, two of RA Survey’s 5 chain Invar bands were cut in half creating 4 nominally 50 metre Invar bands. These bands were considered and later found to be more practical for field calibration.   

 

The technique first required that the precise relationship between electrical resistance and the steel band’s length be determined. Such work was undertaken by the British National Physical Laboratory. The procedure in the field was then to use the 50 metre Invar bands for the actual measurement of the baseline, but to standardise these Invar bands by frequent (morning and evening) comparison with the steel band standards.

 

In the last half of 1939, the RA Survey undertook measurement of the Jondaryan baseline in Queensland, followed by measurement of the Somerton baseline, in New South Wales. Both these baselines were measured using the 50 metre Invar bands and RA Survey’s resistance thermometry technique. Even though the technique was independent of temperature observation, four monitoring thermometers were used throughout the measuring. These thermometers had been carefully calibrated beforehand. The recording of temperature then allowed a limited analysis of the new technique, and the likely error arising from the sole use of mercurial thermometers to determine thermal expansion of the measuring apparatus.

 

Consistent and accurate results were obtained with the probable error of the Jondaryan baseline measurement about one part in two million, and that of the Somerton baseline measurement about one part in 15 million (less than one-fiftieth of an inch in a five mile baseline or 1 millimetre in 15 kilometres). Resistance thermometry produced results to be unsurpassed elsewhere in the world of geodetic surveying (Lawrence, 1939).

 

In 1950, RA Survey also used resistance thermometry when measuring the baseline near Koolymilka in South Australia. Koolymilka was the last baseline to be measured before the advent of electronic distance measuring equipment was introduced and thus the last time resistance thermometry was used.

 

 

 

References

 

Clark, JS and Johnson, LOC (1951), Standardisation of Steel Surveying Tapes, Empire Survey Review, Vol.11, Issue 81, pp.118-128.

 

FitzGerald, Lawrence (1939), Report on the Measurement of the Jondaryan and Somerton Base Lines, published by Army Headquarters, Melbourne, C1015, Government Printer, Melbourne, 1939, accessed at : http://xnatmap.org/adnm/ops/prog\aubaselines/report 1939/REPORT1939.htm

 

Grant, Kerr (1940), Advance in Technique of Modern Survey Work, Age, Saturday 6 July 1940, pp.9, accessed at : https://trove.nla.gov.au/newspaper/article/204405073

 

Hidnert, Peter and Kirby, Richard (1953), A New Method for Determining Linear Thermal Expansion of Invar Geodetic Surveying Tapes, Research Paper 2407, Journal of Research of the National Bureau of Standards Vol.50, No.4, April 1953, pp.179-185.

 

Tomlin, SG (1983), Grant, Sir Kerr (1878–1967), Australian Dictionary of Biography, National Centre of Biography, Australian National University, accessed at : http://adb.anu.edu.au/biography/grant-sir-kerr-6456/text11053

 

 

 

 

Annexure C

Links to those mentioned above where available

 

Name	Link or otherwise
Philip Francis Adams	http://adb.anu.edu.au/biography/adams-philip-francis-2867
Alexander Allan	https://monumentaustralia.org.au/themes/landscape/settlement/display/31399-black-allan-line
George Biddell Airy	https://en.wikisource.org/wiki/1911_Encyclop%C3%A6dia_Britannica/Airy,_Sir_George_Biddell
Cecil Twisden Bedford	https://www.qld.gov.au/recreation/arts/heritage/museum-of-lands/surveying/borders/survey-qld-nt
Arthur Charles Betts	http://www.monaropioneers.com/Betts-ac.htm
Alexander Black	https://monumentaustralia.org.au/themes/landscape/settlement/display/31399-black-allan-line
Augustus James Blakeway	1937 – a surveyor in the Northern Territory Administration
Richard Bourke	http://adb.anu.edu.au/biography/bourke-sir-richard-1806
James Brooks	Other source(s)
James Charles Burnett	http://adb.anu.edu.au/biography/burnett-james-charles-3117
Thomas Burr	https://en.wikipedia.org/wiki/Thomas_Burr
Jacques Cassini	https://www.encyclopedia.com/science/dictionaries-thesauruses-pictures-and-press-releases/cassini-jacques-cassini-ii
Francois Cassini de Thury	https://www.encyclopedia.com/science/dictionaries-thesauruses-pictures-and-press-releases/cassini-de-thury-cesar-fran
Dominique comte de Cassini	https://www.britannica.com/biography/Dominique-comte-de-Cassini
John Sofala Chard	https://www.findagrave.com/memorial/146118032/john-sofala-chard
Thomas Frederick Colby	https://www.libraryireland.com/biography/ThomasColby.php
William Jacomb Conder	https://books.google.com.au/books?id=hciADQAAQBAJ&pg=PA297&lpg=PA297&dq=william+Conder+surveyor&source=bl&ots=7Kkdswvu4L&sig=ACfU3U2t1bsknr3szfts_zRYJXGAoB7hJQ&hl=en&sa=X&ved=2ahUKEwj_1ZS94JXlAhVEjuYKHQLnC0g4ChDoATACegQICRAB#v=onepage&q=william%20Conder%20surveyor&f=false
William Henry Cornish	https://trove.nla.gov.au/newspaper/article/47267297
George Christian Darbyshire	https://en.wikipedia.org/wiki/George_Christian_Darbyshire
William Thomas Denison	http://adb.anu.edu.au/biography/denison-sir-william-thomas-3394
Robert Dixon	https://en.wikipedia.org/wiki/Robert_Dixon_(explorer)
John Henry Driver	1937 – a surveyor in the Northern Territory Administration
Robert Lewis John Ellery	http://adb.anu.edu.au/biography/ellery-robert-lewis-3477
Lawrence FitzGerald	http://www.rasurvey.org/actindex.html
Thomas Florance	http://adb.anu.edu.au/biography/florance-thomas-2051
Edward Charles Frome	http://adb.anu.edu.au/biography/frome-edward-charles-2070
George Woodroffe Goyder	http://adb.anu.edu.au/biography/goyder-george-woodroffe-3647
Augustus Charles Gregory	http://adb.anu.edu.au/biography/gregory-sir-augustus-charles-3663
Charles Hope Harris	https://en.wikipedia.org/wiki/Charles_Hope_Harris
Robert Hoddle	http://adb.anu.edu.au/biography/hoddle-robert-2190
Clement Hodgkinson	http://adb.anu.edu.au/biography/hodgkinson-clement-3774
Robert Hoggan	https://www.qld.gov.au/recreation/arts/heritage/museum-of-lands/surveying/borders/survey-qld-nt
Harry Frederick Johnston	http://adb.anu.edu.au/biography/johnston-harry-frederick-7084
Charles Joseph La Trobe	http://adb.anu.edu.au/biography/la-trobe-charles-joseph-2334
William Lambton	https://en.wikisource.org/wiki/Lambton,_William_(DNB00)
Adrien Marie Legendre	https://www.encyclopedia.com/science/dictionaries-thesauruses-pictures-and-press-releases/legendre-adrien-marie
William Light	http://adb.anu.edu.au/biography/light-william-2359
David Lindsay	http://adb.anu.edu.au/biography/lindsay-david-602
Archibald McDowall	http://adb.anu.edu.au/biography/mcdowall-archibald-7348
George McKay	Other source(s)
Pierre Francois Andre Mechain	https://www.encyclopedia.com/science/dictionaries-thesauruses-pictures-and-press-releases/mechain-pierre-fran
Thomas Livingstone Mitchell	http://adb.anu.edu.au/biography/mitchell-sir-thomas-livingstone-2463
John Joseph William Molesworth Oxley	http://adb.anu.edu.au/biography/oxley-john-joseph-2530
John Moyle Painter	https://www.ancestry.com.au/boards/thread.aspx?mv=flat&m=940&p=surnames.painter
Samuel Parry	https://www.southaustralianhistory.com.au/exploration.htm
John Septimus Roe	http://adb.anu.edu.au/biography/roe-john-septimus-2600
William Roy	https://www.english-heritage.org.uk/visit/blue-plaques/major-general-william-roy/
Robert Russell	http://adb.anu.edu.au/biography/russell-robert-2621
George Robarts Smalley	http://adb.anu.edu.au/biography/smalley-george-robarts-4594
Willebrord Snell	https://www.encyclopedia.com/people/science-and-technology/mathematics-biographies/willebrord-snell
Frank Pettinger Shepherd	Surveyor General of the Northern Territory (1932-1938)
Alan Alfred Spowers	https://www.qld.gov.au/recreation/arts/heritage/museum-of-lands/surveying/surveyors/surveyors-general#allan-alfred-spowers
Charles Todd	http://adb.anu.edu.au/biography/todd-sir-charles-4727
William Turton	Benwell, George L (1991), Tracking Turton in Gippsland, The Australian Surveyor, Vol.36, No.3, pp.227-239.
Edward Twynam	https://en.wikipedia.org/wiki/Surveyor_General_of_New_South_Wales
Charles James Tyers	http://adb.anu.edu.au/biography/tyers-charles-james-2749
Leonard Abington Vessey	Other source(s)
Lawrence Allen Wells	http://adb.anu.edu.au/biography/wells-lawrence-allen-9043
Henry Wood	Other source(s)

 

 

 

Annexure D

 

A Plausible Reconciliation of Mitchell’s Botany Bay Baselines

 

Figure D1: A diagram to explain how, due to a curved shoreline, two baselines, AB and BC of equal length can become a single baseline AC

with the addition of one extra measurement BX.

 

In his publication Thomas Mitchell : Surveyor General and Explorer, Cumpston  (1954) quoted part of a letter from Mitchell to his mother, dated 1 February 1828,…I measured a base of a mile on the smooth sandy beach at Botany Bay yesterday for the purpose of making a grand survey of the whole country. Mitchell thus must have done this work on 31 January 1828.

 

Foster (1985), in his book Sir Thomas Livingston [sic] Mitchell and his World 1792-1855, stated:…In April 1828 Mitchell measured two bases, each of 832 yards on the sandy shore of Botany Bay.

 

Brock (2006) stated something similar:…Mitchell measured two baselines in April 1828 as the foundation for his triangulation survey, each of 832 yards (760.781 metres) in length, along the sands of the shore at Botany Bay.

 

Even though the dates don’t align it seems highly unlikely that Mitchell set down a baseline in January 1828 and then two baselines in April 1828, all for the same purpose and all at Botany Bay. Also, why two baselines of equal length? There seemed to be no advantage of going to the extra effort of making the baseline lengths equal when the amount of following work would be the same no matter what the length of the baselines. The length of 832 yards was also puzzling why not 880 yards which was half a mile (1 mile is 1 760 yards).

 

With the aid of Google Earth, to assist the memory of an onsite visit many years ago, measurements were taken which showed that it was impossible to get a mile of straight beach as the Botany Bay shoreline curves (even accepting nearly 200 years of change). Attempting to fit two lines of 832 yards onto the curving beach in Google Earth, the triangle in Figure D1 above was formed and therein lies a plausible explanation.

 

It was possible that Mitchell, after measuring as far as he could in a straight line, the first 832 yards (AB in Figure D1), then angled the line and proceeded to lay out that same distance again (BC in Figure D1). Thus, there were now two baselines but they were not separate (and nowhere does it say they were), the end of the first being the start of the second. The strange length of 832 yards could now be explained in it being the longest straight line distance possible within the curving beach. With an observer now at say A looking to someone or a marker at C, another person could be directed to be on the line AC and be directly opposite the point B, that is at point X. The distance BX could then be measured. Please refer to Figure D1 above.

 

Mitchell had thus formed two right angled triangles and furthermore because of the equal sides AB and BC, AX would equal CX, so using Pythagoras to calculate either AX or CX, double that result would give the distance AC. Thus, from two shorter baselines, but each being of equal length, a single baseline was determined which approximated the length of the two shorter baselines. This was all done by measurement and no angles needed to be observed. For example, a ten degree kink in the line at B would mean that the distance BX would be some 75 yards giving AC as some 1660 yards, a loss of only 4 yards (832 x 2 = 1664 and only 100 yards short of the mile).

 

Thus, technically it was from two baselines each of 832 yards from which Mitchell obtained a single baseline of about a mile, which is what Mitchell simplified in his letter to his Mother.

 

 

 

 

 

Annexure E

 

Geodetic Survey

The Sydney Morning Herald, Thursday 28 December 1865, Page 2 https://trove.nla.gov.au/newspaper/article/31126250?searchTerm=geodetic%20survey&searchLimits=l-format=Article|||l-title=35|||l-decade=186

 

Government Astronomer to Colonial Secretary.

Government Observatory,

Sydney, 18th August, 1865.

 

Sir, - The following question has for some time occupied my earnest attention - "Considering all the circumstances of the Sydney Observatory, in what way can it for the present be made most generally useful?"

 

1. To my recent report on this Observatory, I have furnished an appendix drawn up by Professor Airy - one of the highest authorities on such matters - and the following remark occurs:-

 

"It is probable that the province of New South Wales, and the continent of Australia generally, may be the scene of important geodetic and hydrographic operations, either for the purpose of territorial survey of a high order, or for the scientific measures of arcs of meridian and arcs of parallel. Works of this class should originate from the Sydney Observatory as starting point."

 

I quite agree with this opinion, and consider that I cannot, in my scientific capacity, serve the interests of the colony better than by the measurement of an arc of the meridian, to serve as a sound basis for the future operations of the surveyor, in carrying out a new and complete triangulation of New South Wales.

 

2. It is, I believe, admitted that there has never been any triangulation of this colony upon which sufficient reliance can be placed; and it is equally certain that such a work, properly carried out, is of the highest public importance.

 

3. To secure its due performance, it is absolutely essential - First, that the baseline should be measured by bars carefully compared with a standard measure, subjected to the most delicate experiments for temperature, and the corrections thus obtained, properly applied; Secondly, that the principal stations should be carefully selected, and have their latitudes and longitudes determined astronomically.

 

With respect to the baseline, to measure it by chains or by rods whose temperature co-efficients are not obtained with rigid accuracy, would be faulty in principle, and would certainly prove fatal in practice.

 

Even a comparatively small error would affect every triangle in the series, and might be so augmented throughout the entire triangulation that little reliance could be placed upon the terminal measurements. Such a proceeding may be likened to a long train of argument founded upon false premises.

 

It is of equal importance that the extremities of the baseline, and, the geographical positions of the principal stations should be determined by astronomical instruments of a superior class.

 

Such a series of stations, selected, as far as possible, along a meridian of the country, and once laid down with the highest attainable degree of accuracy, would become permanent reliable marks, available at any future time for the ordinary surveyor to extend or verify his previous triangulation.

 

4. Such a work as this, requiring as it does a considerable knowledge of pure mathematics and physical science, besides an intimate acquaintance with astronomical observations and calculations, seems to fall within the natural province of the astronomer, whose studies and attention have been directed to such matters as these; and this view has been held in other countries where the same operations have been carried out.

 

5. I wish to express myself clearly that I do not propose to direct a complete triangulation of New South Wales in all its details, or in any way to usurp the natural functions of the Surveyor-General, who with the intelligent and efficient staff at his command, is just as well able to carry out a detailed triangulation as myself.

 

I propose only to construct - if I may use the expression - the "back bone" of the general triangulation, form the definite and reliable points of which the surveyors may either proceed directly, or, if circumstances should render it more expedient, work up to, and thus verify, in the most accurate manner, their own branch work.

 

6. I will designate my proposed operations by the short title of "The Geodetic Survey."

 

It would have for its object the exact measurement of an arc of the meridian, extending, if possible, from the frontier of Victoria to that of Queensland, thus affording new and valuable data for the solution of the problem relative to the figure of the earth. The baseline measured for this purpose would be from six to eight miles in length, and should be determined within a fraction of an inch. The extremities of this line, as well as the series of astronomically determined stations in the vicinity of the meridian, would be identified at any future time by permanent marks, so that they would always be available for future geographical or trigonometrical operations.

 

Moreover, this geodetic survey would comprise the determination of the magnetic bearings and other magnetic elements of each station, as well as their heights above the mean sea level, with an accuracy unattainable by ordinary methods. The practical importance of rigid magnetic observations alone cannot be too much enlarged upon; for not only is it impossible to obtain them without the aid of such delicate instruments as those used in this Observatory, but so great is the local influence in Australia, that it is only by a series of observations carefully made and reduced, that true results for any individual station can be obtained.

 

7. I have thus far endeavoured to point out the importance of a geodetic survey, not only per se, but also in its relation to a retriangulation of the colony.

 

It cannot supersede the latter, but I do think that, to a certain extent, it ought to precede it - especially in the measurement of the baseline. At the same time, it would be quite unnecessary for the general triangulation to be deferred until the termination of the geodetic survey; on the contrary, it might, be commenced at any time, as for some time this work would be quite independent of mine. The one, indeed, is urgently needed for the necessities of the country, the other is equally essential to render it complete and sure.

 

8. I am of opinion that this geodetic survey may be completed with an annual grant of £1000 for five years; and with this view, I recommend that the sum of £1000 be placed upon the Estimates for the year 1866.

 

Most of the instruments required for the purpose are already in the colony, or can be readily obtained; and I believe I may state that the Astronomer Royal of England would willingly render any further assistance that might be needed, in order to carry out what he believes to be a most important work.

 

I have, &c.

George R. Smalley

Government Astronomer.

 

 

 

 

 

Annexure F

 

 

 

Trigonometrical Survey : Interesting Interview :  Wonderful Instruments

Lachlander and Condobolin and Western Districts Recorder, Thursday 13 September 1945, Page 1

https://trove.nla.gov.au/newspaper/article/214476096?searchTerm=Trigonometrical%20Survey%20-%20Interesting%20Interview%20-%20Wonderful%20Instruments&searchLimits=l-state=New+South+Wales|||l-format=Article|||sortby=dateAsc|||l-title=1153

 

 

 

The survey party which has been operating in Condobolin district of recent months has been engaged exclusively on Trigonometrical survey work.

 

In discussing the survey with Mr. C. E. Elphinstone, who is in charge of the party, it was learned that the former Trig, survey was suspended in 1916, after having covered only about one third of the State. During the early part of the present war the need for accurate maps of the coastal areas became acute and trig survey operations were recommenced, particularly on the North Coast and Northern Tablelands, and the work has been effected by Army and Land Department units. A stage has now been reached, when a very precise chain of triangulation needs to be extended from Condobolin to Tamworth via Dubbo and Coonabarabran, and in order to do this a precise check on the old Triangulation system at Condobolin is necessary.   

 

A particularly precise survey has been made at Condobolin, said Mr. Elphinstone. A line 7 miles long was measured to the East of the Experimental Farm, and then a series of 22 triangles were observed in order to extend the precise length of that measured line to three main triangle sides of about thirty miles each in length.

 

The measured line at Condobolin is the fifth one of that nature to be measured in the State. The first one was measured at Lake George in 1870, and this was followed by another near Richmond in 1880. Then of recent years one was measured at Bourke, in 1927, and an Army Unit measured one near Tamworth about 10 years ago. In the two earlier measurements solid iron and wooden bars ten feet long were used in conjunction with microscopes and some nine month’s work was involved; but with the more recent measurements special bands were used and the Condobolin measurement was effected in three weeks, with some adverse weather, too. The bands used in this measurement are of interest. They are 24 metres in length, the metric system being used because the main standard of length for Geodetic work is held at Paris, where a six metre length is preserved in a vault. This standard of length has been conveyed to London, and the bands used at Condobolin were carefully checked for standard length by the Science Laboratory at Teddington, London. Great care is taken to preserve this standard of length by the Lands Department of New South Wales.

 

Following the measurement of this baseline at Condobolin, angular measurements were made by Messrs. Elphinstone and Anderson and this work is now reaching completion. A large theodolite weighing about 2 cwt, is used. This instrument was made by Repsold & Sons, of Hamburg, in 1911, on the design of Sir David Gill, Govt. Astronomer of South Africa, and it is probably the best instrument of its type in Australia.

 

Some idea of the accuracy obtained can be judged from the fact that two measurements of the seven mile line agreed to within an eighth of an inch, and the errors of the angular measurement average about one foot in one hundred miles.

 

This precise triangulation is only effected in strips some 159 miles wide and gives control to secondary triangulation which in turn gives the most satisfactory type of control for detailed and contoured mapping - and the main ultimate object of the work is the production of an accurate detailed contoured map of the State.

 

The work is also of scientific interest, for it is precise triangulation in conjunction with precise astronomical observation which provides the information for computation of the size and shape of the earth's surface. To date triangulation has not extended sufficiently far in Australia to arrive at any conclusive results. Australia offers the best opportunity for research of this nature in the Southern Hemisphere and results are awaited with interest in scientific circles, for it is thought that the Southern Hemisphere is larger than the Northern one.