A Brief Explanation of the
Map Projection and Scale Factor
for a mapping system in the then
Development Area of Albury-Wodonga
(Author and date unknown)
Albury–Wodonga is the broad settlement incorporating the twin Australian cities of Albury and Wodonga. Albury and Wodonga are separated by the Murray River not only geographically, but also politically; Albury to the north of the river is part of New South Wales while Wodonga on the south bank is in Victoria.
Albury-Wodonga was designated a national growth centre when the Prime Minister, Mr Gough Whitlam, the NSW Premier, Sir Robert Askin, and the Victorian Premier, Mr Rupert Hamer, met at Albury-Wodonga on 25 January 1973 and agreed to develop Albury-Wodonga to a population level of some 300,000 around the turn of the twentieth century. One of the reasons why Albury-Wodonga was chosen to become the first centre for national growth or decentralisation was its central location. It is located on a major highway and rail corridor that links Australia’s two major cities of Melbourne and Sydney, making it central to approximately 75 per cent of Australia’s population. The Commonwealth, New South Wales and Victorian governments, in a unique agreement dated 23 October, 1973, recognised the need to encourage more balanced development in Australia and provide an alternative to capital city living.
Under the agreement the two cities were to become one. Aldonga or Wodbury were even proposed as the name for these combined localities. Albury-Wodonga was however born, with the overarching Albury-Wodonga Development Corporation, representing the Commonwealth, Victorian and New South Wales governments.
The plan was to encourage decentralisation by having people move away from the big cities of Sydney and Melbourne especially. As well as enticing some industry to move there, it was the mass movement of public servants that would achieve the aim of the scheme. Curiously, public servants didn't want to move. Then Whitlam’s Labor government was replaced by Fraser's Coalition government which did not have the same interest in the scheme. Eventually the development corporation ceased to exist, becoming nothing but a corporate shell now selling the remaining land it once bought to develop.
At the time however, one of the pressing considerations was the adoption of a mapping system for this area for planning purposes. This high priority decision was necessitated by Victoria having its mapping based on the Australian Map Grid (AMG) while New South Wales mapping used the Integrated Survey Grid (ISG). This internal paper discusses the issues involved in the selection of a mapping system for the development area.
Albury-Wodonga as depicted in : (top) 1941 on Wangaratta 4 mile to 1 inch scale map sheet; (centre) 1968 on Wangaratta R502 series 1: 250,000 scale map sheet; (bottom) 2002 on Wangaratta NTMS series 1: 250,000 scale map sheet
Introduction
The surface of the earth is usually defined mathematically as an oblate spheroid and the precise definition of a point is obtained by expressing its coordinates in latitude and longitude referred to the spheroid. Computations in this coordinate system are difficult for everyday work and it is convenient to project the curved surface on to a plane surface and by a mapping transformation convert the latitude and longitude into rectangular coordinates. It is not possible to make such a transformation without distorting some of the physical relationships between points on the original surface.
In Australia, the Transverse Mercator projection has been adopted as the most convenient transformation to use, having regard to the size, shape and location of Australia on the surface of the earth as well as those physical relationships which it is generally convenient to preserve. It does, however, distort the distance between points and this distortion is a function of the position of points on the projection and the parameters of the projection. The resultant distortion is called the scale factor.
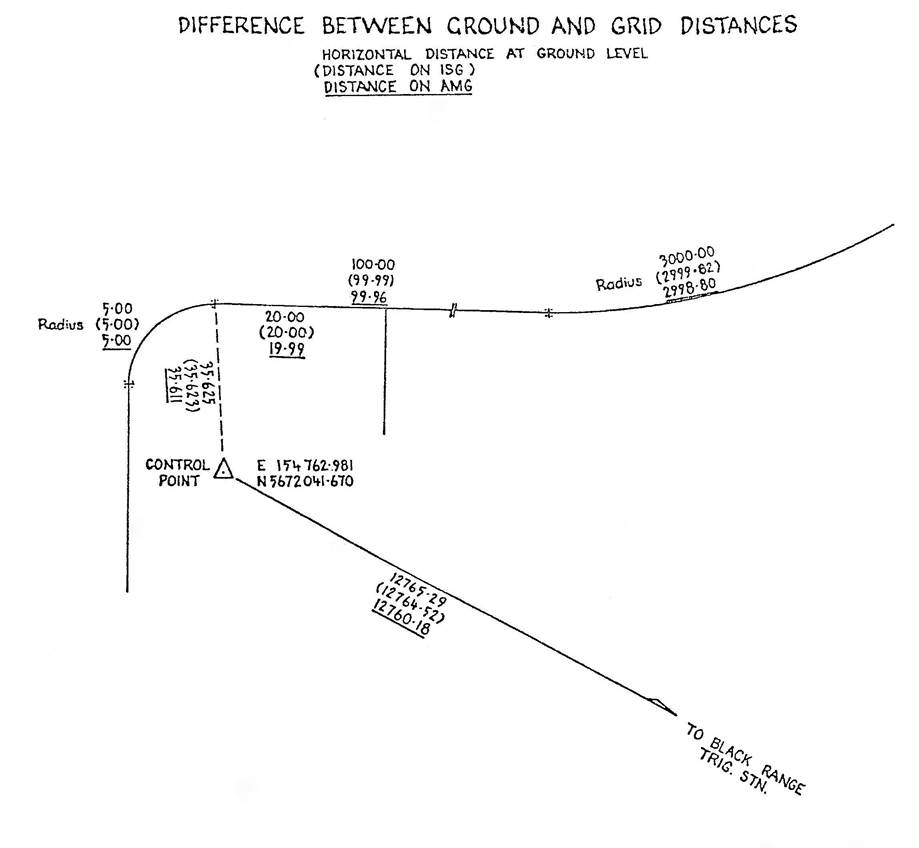
The variations of the projection used in Victoria and New South Wales are known respectively as the Australian Map Grid and the Integrated Survey Grid. These have been selected to suit the requirements of the respective states having regard to the advantages and disadvantages of each. These projections incorporate scale factors which can produce significant differences (up to one part in 2,000 in the case of the AMG and up to 1 part in 17,000 for the ISG) between distances as measured on the ground and as calculated on the coordinate system of the projection.
The presentation of distance on maps and plans is complicated by the existence of the scale factor. Any distance quoted on a map or plan with a coordinate grid should be compatible with the coordinates defining the end points. This grid distance may differ a little from the distance existing on the ground. The difference will depend on the length of the line and the magnitude of the scale factor.
The selection of the projection parameter controlling the scale factor is limited by variables such as height of the terrain above sea level and the distance east and west of the central meridian which are to be mapped. For a limited area such as Albury-Wodonga a special projection can be selected so that the difference between the true and the projection distance does not exceed one part in 100,000. For all purposes, except high order control which only concerns surveyors, grid and ground distance would be the same. No special annotation would be required on plans to indicate the need to convert grid distance to ground distance or vice versa.
Conversion of coordinates between a new system and the AMG or the ISG would be simple matter using existing computer programs with slight modifications.
Map Projection
The projection of the surface of the earth onto a plane surface to produce a map deforms some or all of the physical relationships (distance, direction, size, shape) existing on the earth. The selection of a projection is governed by the purpose for which the map is to be used which in turn determines the physical relationship(s) which it is most desirable to preserve.
Any system of projection will result in some or all of the deformations :
Similar angles at different points on the earth may or may not be shown as similar on the map.
The area of one region may or may not be enlarged or reduced in proportion to that of another.
Distance relationships among all points on the earth cannot be shown without distortion on the map.
Directions among divergent points cannot be shown without distortion on the map.
The Transverse Mercator projection has been adopted in Australia for mapping and coordinate systems. This projection is derived by projecting the surface of the earth mathematically on to an enveloping cylinder tangent along a meridian called the Central Meridian. It is obvious that the further away from the Central Meridian the greater will be the deformation. Accordingly, Australia has followed the Universal Transverse Mercator system which divides the World into zones 6 degrees of longitude in width (550 kilometres at latitude 35°) with a Central Meridian at the centre of each zone. Thus, Australia is covered by strips of projections with the distortion at the edge of each strip being much less than the distortions that would occur using only one projection to cover the whole continent. Each strip is subdivided into areas corresponding to the size of a map sheet. The number of map sheets in a series depends on the scale of the map.
The advantages of the Transverse Mercator Projection are :
small areas are represented by the correct shape, and
a line of constant bearing is represented as a straight line on the projection.
Scale Factor
It can be seen that only along the central meridian will the distance represented on the projection be the same as on the earth (ignoring the reduction to the scale of the map whatever it may be, 1: 250,000 etc). Distances not on the Central Meridian need to be stretched from the surface of the earth to fit on the surface of the cylinder which is opened out to form the plane of the map sheet. The further from the Central Meridian the greater will be the stretching or increase in scale. The scale factor then increases with increasing distance from the Central Meridian.
Scale factor is defined by :
Distance on earth X scale factor = Distance on projection.
A significant property of the Transverse Mercator projection is that scale factor at a point is the same in all directions. This allows angles at a point on the ground to be represented by the same angles on the projection.
The variation of scale factor with distance from the Central Meridian is represented graphically thus :
Grid distance always greater than Ground distance
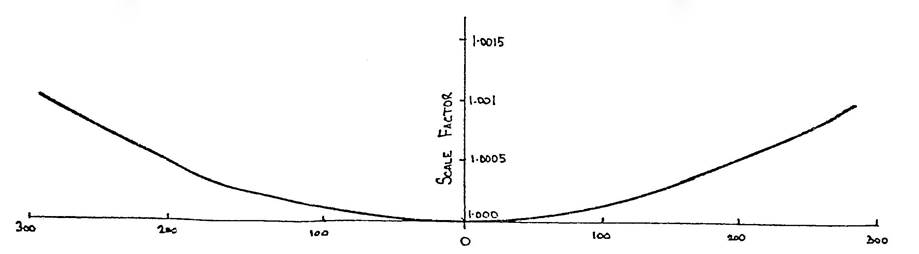
Distance from Central Meridian (km)
The curve is a parabola and the scale factor increases with the square of the distance from the Central Meridian.
At the edge of a 6° zone the scale factor (at the latitude of Albury) is approximately 1.001, ie a difference-of one part 1 in 1,000. This means that a line 1000 metres long on the ground at sea level would have to be shown on the projection as 1001 metres and coordinates defining the ends of the line must produce a length of 1001 metres.
Because this difference between true and projection distance was large a negative scale factor was imposed on the Central Meridian. This is represented by projecting the surface of the earth on to a cylinder not tangential along the Central Meridian but intersecting the surface of the earth along two small circles parallel to the Central Meridian and equidistant on either side. The variation of scale factor is then represented as :
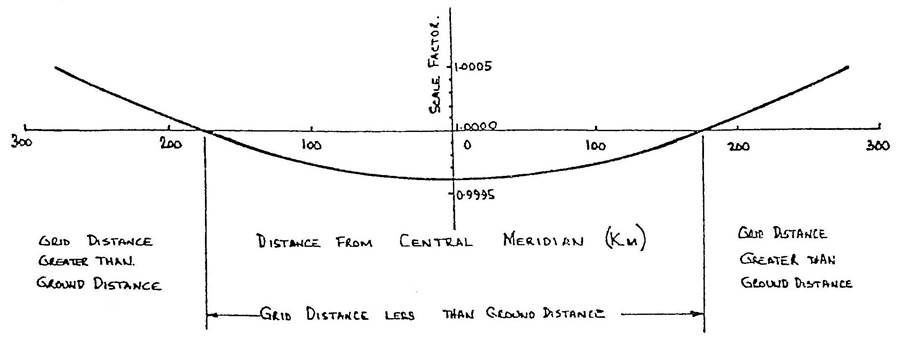
The negative scale factor adopted for the 6° zones in Australia was 0.9996, a scale reduction of 1 part in 2500. This results in a scale factor of approximately 1.0005 at the edge of the zone in the latitude of Albury.
The resulting projection is known as the Australian Map Grid and was adopted by the National Mapping Council in 1965 for the production of maps at the scales of 1:250,000, 1: 100,000, 1: 50,000 and 1: 25,000. For a zone 6° of longitude in width it is not possible to reduce the scale factor at the edge of the zone any further without decreasing the central scale factor.
For national mapping purposes at relatively small scales (less than say 1:25,000) a scale factor of 0.9996 presents no problems. In the production however, of large scale maps (greater than 1: 10,000) and on surveys of small (in extent) areas which are comparatively precise and detailed, the problem of representing on the plan (or map) measurements on the ground, does arise. Do we write the measured distance on the face of plan/map which will be inconsistent with the coordinate grid of the plan/map or do we use the grid or projection distance which is not the true distance in which we are interested? The difference between the two will be 1 part of 2,500 on the central meridian which is less than the required accuracy of engineering and cadastral surveys.
To reduce this difference between true and grid distance, New South Wales has adopted a Transverse Mercator Projection with 20 zones known as the Integrated Survey Grid. The scale factor lies between 0.99994 and 1.00004 and is generally acceptable to engineers because the maximum difference between true and grid distance is only one part in 17,000. All maps/plans in New South Wales at a scale of 1:10,000 or larger are plotted on the ISG. Victoria, however, has adhered to the AMG for the purpose of integration of all surveys and mapping.
Coordinate System
The adoption of a coordinate system is intimately tied in with the choice of zone width and scale factor. Each zone on the AMG for example, has its own system of rectangular coordinates with its own origin. The origin is the intersection of the Central Meridian with the equator and is selected so that rectangular coordinates (East and North) can be related to geographical coordinates (latitude and longitude). To avoid the use of negative numbers or prefixes (North, South, East, West) a False Origin is adopted so that all coordinate values will be positive and that east coordinates will never be similar to north coordinates. The False Origin for AMG zones is 10,000,000 metres south and 500,000 metres west of the True Origin. Coordinates of a point depend on its grid distance from the origin which varies with the choice of Central Scale Factor.
Effect of Height above Sea Level
The figure adopted to represent the surface of the earth is an oblate spheroid. It is a figure which can be defined exactly in mathematical terms and its parameters can be selected so that it approximates very closely the size and shape of the earth. As the earth is covered mainly by the oceans the spheroid selected coincides very nearly with sea level in the oceans and represents sea level under the continents. Any measurement on the ground is therefore made some distance above the reference spheroid or sea level. In any calculation of position on the spheroid and hence on any projection derived from the spheroid, correction must be made to convert the ground measurement to its corresponding length on the spheroid.
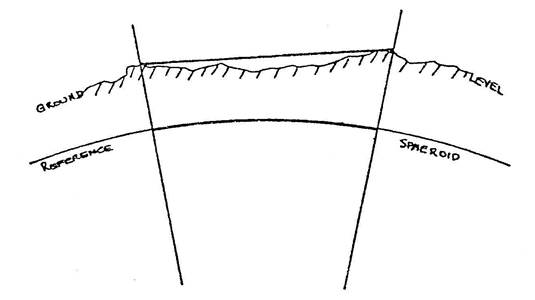
The size of the correction is a function of the length of the line, and the height above sea level. An approximate value of the correction in the area of Albury-Wodonga is 1 part in 35,000 (3 millimetres in 100 metres) adopting an elevation of 180 metres.
To simplify calculations on the projection the height scale factor can be combined with the central scale factor to produce a combined scale factor. This would only apply over a limited area where the variation from the assumed general height above sea level is not large.
Development Area of Albury-Wodonga
The above issues were all considered when a system for mapping in the Development Area of Albury-Wodonga on the Victorian-New South Wales border was to be decided but never eventuated. The choices were :
- The Australian Map Grid
- The Integrated Survey Grid
- A special local [1genmap/actgrid/actgrid.htm] system similar to that used in the Australian Capital Territory
1. The Australian Map Grid
Advantages : This projection is used by the majority of Australian states including Victoria. The use of a single system of projection will enable the integration of all surveys and facilitate the establishment of a land data bank. There would be no confusion about the projection on which any set of coordinates were based.
Disadvantages : The difference between grid distance and ground distance can be quite large and could lead to confusion. In carrying out surveys every distance will need to be converted from grid to ground and vice versa.
2. The Integrated Survey Grid
Advantages : The correction for scale factor can be ignored in many small surveys depending on the standard of accuracy required. The size of corrections is generally small and there is a small rate of change which means that a single value of scale factor can be adopted for a larger survey.
Disadvantages : Corrections from grid to ground and vice versa although small will need to be made in many instances.
3. A Special System
A local system could be introduced for the whole Development Area in which scale factor and sea level correction are incorporated so that there is no difference between ground and grid distance for all work except high order surveys with which only surveyors are concerned. Any map/plan user would not be required to concern themselves with grid and ground distance as they would be the same.