Papers relating to The Boundary Line between South Australia and Victoria –
presented to both Houses of [Victorian] Parliament by his Excellency’s Command :
a prelude to the Disputed Territory
“There is still more serious objection to alter the present boundary…to transfer, without their consent, a large number of people, who, in reliance upon the legality and the permanence of the boundary line, elected to settle upon Victorian soil, and to live under Victorian laws. It seems that the claims of good faith towards these people are not less weighty than those of theoretical accuracy in determining a meridian….when a settled population has become established the interests and the rights of private persons demand attention”
James Joseph Casey (1831–1913), Minister of Lands and Agriculture, and President of the Board of Land and Works, Department of Lands and Agriculture, Melbourne, 25 July 1874.
An extensive review by Paul Wise, 2024.
Longitude of Fort Macquarie, Sydney
The 1839 line by Tyers and Townsend or Tyers’ Line
The 1847-1850 line by Wade and White or Wade’s Line
1865 Gazetteer Map of Victoria
Longitude by (Electric) Telegraph
1868 Boundary Determination by Telegraph
Wade and White’s Chaining Clarified
Adopting a Common Datum for the above Surveys
Papers relating to The Boundary Line between South Australia and Victoria (hereinafter just called the Papers) was a twenty-eight page document plus two plans, printed and bound in 1874. Only eight hundred copies were produced at that time by John Ferres, Government Printer, Melbourne. As their title suggests the document was prepared for the consideration of the Victorian Parliament.
The first half of the Papers contained copies of Correspondence between the Governments of South Australia and Victoria relating to the determination of the Boundary Line. An appendix completed the publication, titled Report on the Determination of The Boundary Line of the Colonies of South Australia and New South Wales, by Charles Todd, F.R.A.S., Observer and Superintendent of Telegraphs, South Australia. The report included the two plans and concluded with a short Joint Report by Messrs. Smalley And Todd, formally accepting the results of their boundary determination on behalf of their respective New South Wales and South Australian State Governments in 1868.
The history of the contents of these Papers evolved from the efforts in marking the Boundary between the then Colonies of New South Wales and South Australia. The first attempt was in the south, between the Southern Ocean and River Murray, along what was to become the border between Victoria and South Australia and later north of the River Murray to 26 degrees south latitude, between South Australia and New South Wales.
The Boundary between these Colonies was the 141st meridian (141 degrees east longitude) as determined by an Act on 15 August 1834, to erect South Australia into a British Province or Provinces and by Letters Patent...did hereby fix the boundaries of the same Province... on the north the 26 degrees of south latitude, on the east the 141 degrees of east longitude. The Colony of Victoria, previously the Port Phillip District of New South Wales, was separated from New South Wales with the issue of writs of 1st July 1851, for election of members of Council for Victoria, being the legal symbol of this separation. As the South Australian eastern limit was already decreed the western limit of the Colony of Victoria became 141 degrees east longitude by default.
Thus, in the early days (before 1851) of the Boundary determination at 141 degrees east longitude, it was the New South Wales administration who made the decisions in their best interests leaving Victoria after 1851 with the legacy of those New South Wales verdicts.
The need for a clear line of demarcation between adjoining administrations was fundamental to the whole operation of bureaucratic management. Responsibility for land tenure, taxation, law and order, infrastructure, census, and dutiable goods movement were just some aspects that required defined and recognised geographical limits to operate effectively and with clarity.
As settlement encroached into the region and irreconcilable differences of the location of the 141st meridian started to be depicted on maps of the time, Colonial Surveyor Charles James Tyers (1806-1870) was commissioned in 1839 by Sir George Gipps (1790-1847), Governor of New South Wales, to ascertain its actual location. Based on Tyers’ determinations using the best technology of the day, a provisional boundary (Tyers’ Line) of only some 3½ miles was marked in 1839 (the line was longer but was naturally not marked where it crossed the waters of the Basin of the River Glenelg). As part of Tyers’ brief he also fixed the position of the eastern bank of the mouth of the River Glenelg. When all Tyers’ survey results were compiled he determined that the 141st meridian was some 1¼ miles west of the mouth of the River Glenelg. Tyers had served in the British Navy and was a skilled marine surveyor recognised for having computed longitudes in the English Channel, Mediterranean, West Indies and South Africa. He left the navy in 1839 to join the New South Wales Colonial Service as a surveyor. Tyers was more than ably assisted by Thomas Scott Townsend (1812-1869). Townsend had experience with land surveys exploiting the Gunter’s chain for distance measurement. Among other duties he was responsible for chaining the distance from Geelong to Portland and beyond, for Tyers.
Tyers had transferred the longitude of Fort Macquarie in Sydney to Batman’s Hill in Melbourne by the method of chronometric transportation, exactly as he would have done to find longitude at sea. Unfortunately, the longitude of Fort Macquarie, whilst thought to be absolutely reliable, was in fact in error but the amount of error took time to resolve. During this period Captain John Lort Stokes (1812-1885) in command of HMS Beagle, Captain Owen Stanley (1811–1850) in command of HMS Britomart and Thomas Livingstone Mitchell (1792-1855, later Sir and often referred to as Major Mitchell) determined positions further west for the Glenelg than Tyers’ location, which the New South Wales administration saw as advantageous for their gaining of greater territory. At the later High Court hearing in 1911 Pietro Paolo Giovanni Ernesto Baracchi (1851-1926) then the Government Astronomer of Victoria explained that the greatest source of error in the earlier astronomical observations were from errors in the nautical calendar caused by the then imperfect knowledge of the motions of the moon, which had then not yet been resolved. Details of Baracchi’s explanation are provided further on.
By early 1846 the progress of pastoral settlement from Portland and The Glenelg in the east, and eastern parts of South Australia in the west, meant that settlers from the two colonies had begun to encounter each other. In November 1846 by direction of the Colonial Secretary of New South Wales, Mr Wade, a surveyor, was instructed to report himself to Mr Latrobe in order to his being employed in marking a boundary for police purposes between the Port Phillip District of New South Wales and the Province of South Australia (Charles Joseph Latrobe (1801–1875, also La Trobe), was then Superintendent of the District of Port Phillip of New South Wales, being created in 1839, and which later became the Colony of Victoria in 1851).
Surveyor Henry Wade (1810-1854) and South Australian government surveyor Edward Riggs White (1817-1853) met at the mouth of the River Glenelg in 1847. Wade chained due west, establishing a stone mound on the line of the new boundary, avoiding having to chain across the River Glenelg and not as reported elsewhere chaining along the coast where he would have had to chain across the river. Wade and White marked the new boundary (Later Wade & White’s Line or just Wade’s Line) to within some 155 miles of the River Murray. White was to later complete the line. Being in three parts the boundary marking took from 1847 to 1850, due to the country, drought conditions and logistical problems, and both men and their parties endured great hardship. An accepted line of demarcation was proclaimed in the 1847 South Australian Government Gazette on page 411.
Robert Lewis John Ellery (1827-1908) was Superintendent of the Melbourne Astronomical Observatory, when in 1858 Ellery was given carriage of the Geodetic Survey of Victoria. Geodetic quality triangulation was extended over the whole of Victoria with the exception of the north western mallee section. The north east region triangulation was by Alexander Black (1827-1897), the south west work by Alexander Charles Allan (1831-1901) and from 1862 to 1874, William Turton (1828-1906) undertook triangulation in the Gippsland area. Allan’s work included survey stations that would later enable the South Australian and Victorian state geodetic networks to be connected. When occupying Mt Ruskin near Wade’s Line in May 1865 Allan connected his survey to nearby Wade’s Mounds. An example of such connections was shown on this Diagram being No. 10 of the set of the triangulation of Victoria. An 1865 map titled Gazetteer Map of Victoria, published with the permission of the Surveyor General by the Lands and Survey Department, Melbourne, depicted two lines, one of which was described as 141st meridian as defined by Mr Edward White, and marked on the ground, the other as Boundary between Victoria and South Australia being the 141st meridian as adopted by Arrowsmith.
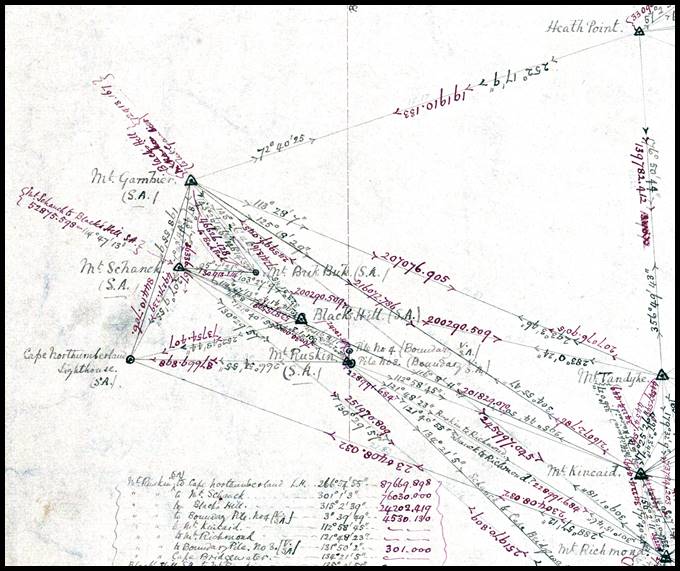
Section of Diagram No10, full map at link above, showing information on connections from Mount Ruskin to Wade’s Mounds/Piles 3 and 4; note distances are in feet.
There subsequently followed further correspondence between South Australia and New South Wales. Sir Henry Parkes (1815-1896), Colonial Secretary of New South Wales, in his reply to South Australia included a copy of a report from the Surveyor General of New South Wales. The Surveyor General, whilst agreeing that the method proposed by South Australia for determining the boundary line between the two Colonies, north of the River Murray, was the most economical and expeditious, being only a prolongation of the existing boundary between South Australia and Victoria, went on to confirm that there were doubts as to the identity of such line with the true geographical boundary of the Colony viz. the 141st meridian. After discussing how the probable error might have occurred and agreeing that the then best available technology had been employed at the time, he concluded that improved positional accuracy was now obtainable by the use of telegraphic signals, and referred to the approaching completion of telegraphic communication between Sydney and Adelaide. (Adelaide and Melbourne had a telegraphic link by mid 1858 and by October 1858 Sydney, Melbourne and thus Adelaide were connected. Adelaide and Sydney did not have a direct link until 1867).
At the River Murray, this line, now forming the border between South Australia and New South Wales, was found to be 3.6 kilometres east of Wade’s Line. However, Wade’s Line was found to run at first east then west of true north. Also the distance of Wade & White's Line off the 141 meridian was less at the coast than at the Murray. The strip of land of then some 332 800 acres (520 square miles, 1347 square kilometres), between Wade & White's Line and the new position of the 141st meridian became known as the Disputed Territory.
South Australia brought a case against Victoria in the High Court of Australia and its loss was then appealed to the Judicial Committee of the Privy Council in November 1913. The appeal being dismissed in January 1914. Of note here is that South Australian Government Surveyor Theodore Ernest Day (1866-1943), later Surveyor General, undertook the survey for the disputed boundary case. His 1911 survey was the last to provide a definitive connection between Wade’s Line and Tyers’ Line as Tyers’ marks have only been located by GPS inference in this era. Day found that Wade’s Line was just short of 3 kilometres west of longitude 141 degrees east.
During this review it was found that confusion today existed as to Tyers’ use of chaining, the location of Tyers’ survey (trigonometric, chronometric, astronomic and chaining) marks, what was proclaimed as the boundary between South Australia and then New South Wales, and whether Day’s survey revealed an error in Wade and Whites’ chaining. The following discussion aims at resolving that confusion and clarifying some other misinformation, including numerical conversions, published elsewhere. Any question as to whether the territory should still be disputed is then left to others!
While the Papers provided some numerical facts, as in the background above much is just rounded for convenience and a few metres here or there is of generally no interest. However, the numbers do tell another story in that those who undertook this work did so with all the care and skill the technology of their respective eras allowed. As all is metricised today the immediate reaction is just to convert all old measurements. In doing so, however, original accuracy can be lost and rounding for ease can destroy meaningful comparisons. Original units are thus used in this next section with metric equivalents given, as necessary.
For reference :
|
1 chain |
100 links |
|
1 chain |
66 feet |
|
1 chain |
20.1 metres approximately |
|
10 chains |
1 furlong |
|
80 chains |
1 mile |
|
8 furlongs |
1 mile |
|
1 mile |
1.60934 kilometres |
|
1 second of arc |
137 links approximately at 38 degrees latitude |
|
1 second of time |
15 seconds of arc (24 hours in a day corresponding to 360 degrees in a day’s rotation) |
|
For clarity in writing the unfamiliar distances of miles, chains and links, when not quoting original distances 2 miles 75 chains 80 links will be written as 2 miles 7580 links. |
|
In the following, the surveys of Tyers and Townsend, Wade and White, and Day will be analysed with the aim of converting their results to a common datum so as to assess their common accuracy.
Longitude of Fort Macquarie, Sydney
Unknowingly, the incorrect longitude for Sydney had been derived in the early years. By adopting this incorrect starting value, Tyers’ value for his line was thus also incorrect.
Lieutenant James Cook first derived the longitude of Fort Macquarie, Sydney. The Sydney Opera House now stands on this site.
|
|
|
|
Fort Macquarie, Sydney, circa 1870. |
Relative locations in 1855 of Fort Macquarie (blue circle) and Fort Phillip later site of Sydney Observatory (green circle). |
Being close to Sydney harbour, Fort Macquarie became the first principal meridian in Australia. During Captain Robert Fitzroy's (1805-1865) famous (by having Naturalist Charles Robert Darwin aboard) second voyage in HMS Beagle in 1831-36 it was one of the points for which longitude was derived. The Beagle’s second voyage determined the longitude of points around the globe by transportation of chronometers (a clock especially designed to be minimally affected by external factors and therefore able to maintain time more accurately). The longitude determined for Fort Macquarie was 151º 08’ 2.10’’.
At the High Court hearing of the Boundary Dispute in 1911 Pietro Paolo Giovanni Ernesto Baracchi (1851-1926) then the Government Astronomer of Victoria explained that the greatest source of error in the earlier observations were from errors in the nautical calendar caused by the then imperfect knowledge of the motions of the moon, which had not yet been resolved. He then quoted the following list of longitude values.
|
Observer & year |
Reported longitude of Fort Macquarie |
|
Lieutenant James Cook, c.1770 |
151 deg 15 min 11 sec |
|
Lieutenant William Dawes, 1787 |
151 deg 18 min 50 sec |
|
Lieutenant William Bradley, 1787 |
151 deg 20 min 38 sec |
|
Broughton and Crosbie, 1787 |
151 deg 09 min 03 sec |
|
Captain John Hunter, 1788 |
151 deg 19 min 42 sec |
|
Admiral Don Jose D’Espinosa, 1793 |
151 deg 12 min 45 sec |
|
Admiral Maracinno, 1793 |
151 deg 17 min 55 sec |
|
Captain Mathew Flinders, 1795 |
151 deg 17 min 12 sec |
|
Captain Mathew Flinders, 1802 |
151 deg 11 min 49 sec |
|
De Fresighy, 1802 |
151 deg 08 min 32 sec |
|
Captain James King, 1887 |
151 deg 17 min 29 sec |
|
Carl Ludwig Christian Rümker, 1822 |
151 deg 17 min 30 sec |
|
Sir Thomas Brisbane, 1822 |
151 deg 15 min 32 sec |
|
Mean |
151 deg 15 min 16 sec |
|
Later longitudes for easy comparison |
|
|
Tyers 1839 adopted |
151 deg 15 min 14 sec |
|
Stokes 1842 adopted |
151 deg 16 min 00 sec |
|
Abbott 1875 published |
151 deg 14 min 00 sec |
|
Later longitudes for easy comparison of Sydney Observatory Longitude difference Fort to Observatory was stated by Arrowsmith (1841) as 49.38 chains west (993.4m or 38.7 arc seconds) |
|
|
First listing in Nautical Almanac 1865 |
151 deg 14 min 57.90 sec |
|
Todd, Smalley & Ellery 1868 found |
151 deg 12 min 14.55 sec |
|
1883 by telegraph from Greenwich |
151 deg 12 min 23.10 sec |
|
1912 |
151 deg 12 min 23.10 sec |
|
1933 |
151 deg 12 min 17.85 sec |
|
1966 (AGD66) |
151 deg 12 min 12.31 sec |
In the Papers, the 1874 Memorandum by Surveyor General Alexander John Skene of Victoria stated that an analysis of documents in the Hydrographic Office, between 1788 and 1851 by numerous navigators and astronomers, places Fort Macquarie, 151° 15’ 05” and that as determined at the observatory, Sydney, amounting nearly to two minutes of space. This 2 minutes of arc (later refined to 2’ 16”) discrepancy amounted to almost 3 kilometres in distance and as will be detailed accounted for much of the error in Tyers’ 1839 location. Clearly, Tyers’ adoption of the value of longitude for Fort Macquarie was entirely correct and based on some seventy years of observations by what were, then and now, recognised as skilled men of their craft.
The 1839 line by Tyers and Townsend or Tyers’ Line
New South Wales Surveyor Charles James Tyers was commissioned in 1839 by Sir George Gipps, Governor of New South Wales, to firstly determine the exact position of the Boundary Line between New South Wales and South Australia and also the position of the River Glenelg. Tyers used three survey methods on his tasks; Triangulation from Melbourne, Chronometric measurement from Sydney (consider this to be finding longitude on land as one would at sea using a clock), and Lunar observations near the Boundary. He was equipped with all the required observational instrumentation; theodolite, sextant and artificial horizon, compass and circumferenter. His pocket chronometer was lent to him by Gipps but he recorded that he also had access to a chronometer by Widenham and a chronometer from Captain Hart, of the brig Rapid, when his primary timepiece failed him.
In Melbourne Tyers was joined by Assistant Surveyor Thomas Scott Townsend. For whatever reason, Townsend’s contribution to Tyers’ success is hard to find and hence his chaining work lacks appropriate consideration. Because of his background Tyers was more accustomed to the deck of a ship than the Australian bush or any land based survey for that matter. While his navigational skills were eminently transferable to the land, distance measurement with a 100 link Gunter chain and chaining party would have been new to him. Townsend’s experience with land surveys exploiting the Gunter’s chain for distance measurement filled that skill gap. While not mentioned by Tyers it was Towsend who probably supplied at least two 100 link chains (generally one for work and the other as a comparative standard) and the associated chaining equipment.
Reported instances of chaining briefly mentioned by Tyers were :
|
1. |
The approximate longitude of Mr Henty’s Flag Staff, (mean of Pyramus chronometer, Mr Assistant Surveyor Townsend’s chain survey from Geelong, and the trigonometrical survey from Melbourne, worked up roughly) is 144° 35’ 52” E;
|
|
2. |
We proceeded towards the Glenelg, fixing daily the position of the camp, by latitude and meridian distance from Portland Bay, both by chronometer and Mr. Townsend’s chain work reduced…we commenced measuring a true north line from the spot found to be 35’ 52” of longitude west of Portland Bay by Mr. Townsend’s chain measurement;
|
|
3. |
The difference of longitude 2’ 19” between Henty’s Flag Staff and Mount Eckersley had been previously measured trigonometrically and with chain.
|
When chaining instances (1) and (2) above are carefully interpreted it is realised that the distance from Geelong to the Basin of the Glenelg, via Portland was chained; in total some 200 miles or 300 kilometres. Although Tyers did not describe the chaining in as much detail as the other methods it was probably because this chaining only acted as a real time check on chronometrically derived distance, as is described by Tyers, and to a lesser extent vice versa. Overall, the chaining provided Tyers with the likely magnitude of the final values from his observations and alerted him to any possible problems as they arose.
In establishing the position of his boundary line Tyers’ stated as the position of the 141st degree of longitude could not be correctly determined until the completion of the trigonometrical survey, and the measurement from hence to Melbourne by chronometer, combined with some astronomical observations which I hoped to make at Portland Bay, I did not anticipate a nearer approximation than a mile; but by ascertaining subsequently the exact longitude of this approximate meridian, I apprehended no difficulty in fixing the true one, by means of the chain and circumferenter. Tyers thus understood from the outset, that while the other survey methods would yield a greater accuracy in position they would also take longer to finalise, thus chaining with chronometric and approximate trigonometrical determinations provided the almost instant positional result he required.

Section of 1840 map of Trigonometrical survey of part of the country between Melbourne and The River Glenelg by CJ Tyers Surveyor & TS Townsend Assistant Surveyor,
with the trigonometrical baselines depicted in blue,
the complete map may be viewed at https://catalogue.nla.gov.au/catalog/1942431, National Library of Australia.
Having clearly established that the approximate longitude of Mr Henty’s Flag Staff, (mean of Pyramus chronometer, Mr Assistant Surveyor Townsend’s chain survey from Geelong, and the trigonometrical survey from Melbourne, worked up roughly) was 144° 35’ 52”. Tyers then stated that under these circumstances we commenced measuring a true north line [Tyers’ 141 degrees east] from the spot found to be 35’ 52” of longitude west of Portland Bay by Mr Townsend’s chain measurement. From the sea coast it passes ten chains west of a high sandy hillock, (the south and west sides of which are quite bare), over one of the same range not quite so high, (on this we made a hole one foot deep and three long in the shape of a broad arrow [later Tyers’ Arrow] , which we filled with limestone). Please refer to Tyers’ account at the Annexure.
Further on, Tyers’ stated from a sand hill two hundred yards east of the marked line, I obtained angles and true bearings to Bridgewater hill, Richmond hill, and Mount Kincaid; by which I was enabled to connect the trigonometrical survey thus far.
From these two statements by Tyers it can be seen that :
his true north line (Tyers’ Line) originated from the spot found to be 35’ 52” of longitude west of Portland and passed ten chains west of a high sandhill, in the same range as this high sandhill, but on a lower sandhill, they made a hole in the shape of a broad arrow (Tyers’ Arrow) and filled it with limestone, and
from a sandhill two hundred yards east of the marked line (Tyers’ Line) he obtained observations which enabled him to connect to his trigonometric survey,
meaning that the sandhill on which the limestone arrow was placed, and his line north commenced, was not only west of a higher sandhill from which he connected to his trigonometric survey, but these two locations were separated in distance quoted as ten chains in one case and 200 yards in another. Tyers’ descriptive distances are comparable as ten chains was 1 000 links and 200 yards converted to 909 links. The annotated map below shows the relativity of these two locations. This matter is further discussed in the section on Day’s survey of 1911.
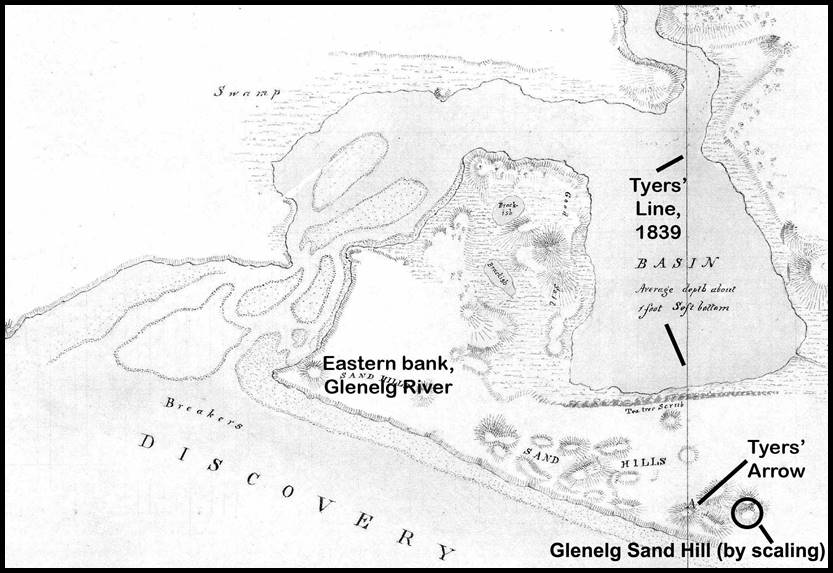
Annotated section of map of Survey of the Lower Part of the River Glenelg copied by Edward Kennedy,
showing the position of Tyers’ Arrow, Line, the Glenelg Sand Hill (approximately) and the eastern bank of the River Glenelg.
Crucially, only one of the two locations, the Arrow, was marked and later found, yet Tyers’ position for his Arrow was only ever documented as being 35’ 52” from Portland but later was accorded the same Lunar longitude, 141° 02’ 54”, as that of the Glenelg Sand Hill. Unfortunately, the fact that only one location was marked and became the focus of further work, that both locations became coincident with the longitude of the Glenelg Sand Hill being adopted as the longitude of Tyers’ Arrow and Line. While the 10 chains/200 yards (some 8 arc seconds of longitude) may have not been significant initially there seems to have been an impact in later years, as will be discussed.
As is detailed in the table below, Tyers’ documents positions for the Glenelg Sand Hill and then the east entrance of the River Glenelg to the sea.
|
Location |
Chronometric Longitude, DMS |
Trigonometric Longitude, DMS |
Lunar Longitude, DMS |
||||||
|
|
Observed |
||||||||
|
Fort Macquarie, Sydney |
151 |
15 |
14 |
|
|
|
|
|
|
|
Batmans Hill, Melbourne, outgoing |
144 |
59 |
00 |
|
|
|
|
|
|
|
Batmans Hill, Melbourne, on return |
144 |
59 |
20 |
|
|
|
|
|
|
|
Batmans Hill, mean adopted |
144 |
59 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
141 |
38 |
38 |
|
|
Camp near (Tyers’ Arrow) Sand Hill |
|
|
|
|
|
|
141 |
03 |
08 |
|
|
Derived |
||||||||
|
Mount Eckersley |
141 |
40 |
04 |
141 |
40 |
16 |
|
|
|
|
Henty’s Flag Staff |
141 |
37 |
45 |
141 |
37 |
57 |
141 |
38 |
01 |
|
Glenelg Sand Hill* |
141 |
02 |
39 |
141 |
01 |
24 |
141 |
02 |
54 |
|
Glenelg Sand Hill** - MEAN |
|
141 |
02 |
19 |
|
||||
|
East point, entrance to the Glenelg*** |
141 |
01 |
43 |
141 |
00 |
28 |
141 |
01 |
59 |
|
East point, entrance to the Glenelg – MEAN |
|
141 |
01 |
23 |
|
||||
|
|
Checked |
||||||||
|
Glenelg Sand Hill – Stanley**** |
141 |
02 |
50 |
141 |
02 |
21 |
|
|
|
|
Glenelg Sand Hill – Stanley**** - MEAN |
|
141 |
02 |
35.5 |
|
||||
|
|
John Arrowsmith (1790-1873) |
||||||||
|
Mouth of the Glenelg (1841)***** |
|
140 |
56 |
55 |
|
||||
|
Notes : (*) Glenelg Sand Hill was a sand hill two hundred yards [8” of arc] east of the marked line, I [Tyers] obtained angles and true bearings…by which I was enabled to connect the trigonometrical survey. (**) This mean value became the longitude of Tyers’ Line and Arrow even though it was not strictly correct. (***) In all three computations Tyers applies the chronometrically derived value of 56” as the longitude difference between that of the Glenelg Sand Hill and that of the river entrance. (****) Captain Owen Stanley, HMS Britomart, at Sydney Cove May 1840 whom Tyers had check his computations with the above results and who stated that I am sorry that I have not had time to go through all the lunars, but those I have worked, give the same results as yours. (*****) John Arrowsmith, geographer/cartographer proposed this value based on his revised value for the longitude of Melbourne to which he applied Tyers’ trigonometric distance to the Glenelg River : https://en.wikisource.org/wiki/Dictionary_of_National_Biography,_1885-1900/Arrowsmith,_John_(1790-1873) |
|||||||||
Of necessity, because of their complexity, the above results were derived after Tyers had returned to Sydney from the Basin of the Glenelg. From the mean of his chronometric, trigonometric and Lunar longitudes he found that the east bank of the entrance to the River Glenelg was at 141° 01’ 23”. This meant that the entrance was 1’ 23” or 1¼ miles (about 2 kilometres) inside New South Wales. An 1840 plan of the Principal Triangles of a Trigonometrical Survey between Melbourne and The Glenelg founded upon Astronomical Bases and signed by Tyers may be viewed via this link.
Captain Owen Stanley, HMS Britomart, at Sydney Cove in May 1840, whom Tyers had check his computations, reported that while he had been only partially able to check Tyers’ Lunar longitudes, his mean for the chronometric and trigonometric longitudes was 141° 02’ 35.5”. The New South Wales administration would have been pleased to hear this as it now meant that the east bank of the entrance to the River Glenelg was now over 1½ miles (about 2.4 kilometres) inside New South Wales.
Captain John Lort Stokes, then in command of HMS Beagle, in1842 performed his own observations for position at Portland and evaluated the preceding work by Tyres to determine his own position for the mouth of the River Glenelg. He positioned Henty’s House (presumably close to the flag staff used by Tyers) at 38° 20' 45" south latitude and 9° 36' 22" west of Sydney.
Stokes noting that Tyers had measured the difference in longitude between Henty's house and the east entrance point of the River Glenelg by triangulation, chronometer, and lunar observations, adopted the triangulated results as the most accurate of the three methods. Tyers’ result for the difference in longitude between the Henty house and Glenelg entrance was 37' 29", which when added to Stokes own value of 9° 36' 22" west of Sydney, for the Henty house, meant that the east entrance point of the River Glenelg was west of Sydney by 10° 13' 51". Please see table below for the numerical detail.
From Tyers’ triangulated longitudes, Stokes found that the difference in longitude between Batmans Hill and the entrance point of the River Glenelg was 3° 58’ 42” to which he added his own value of 6° 16’ 17" for the longitude difference between Batmans Hill and Sydney. The result of this method shows that the east entrance point of the River Glenelg was west of Sydney by 10° 14' 59".
Now taking Stanley's calculation (from checking Tyers and using Tyers' triangulation from Batman's Hill to the east entrance point of the River Glenelg being 3° 57’ 45”) which, together with Stokes' own measurement of the difference of longitude between Batman's Hill and Sydney of 6° 16’ 17", gave the east point of the River Glenelg to be west of Sydney by 10° 14' 02". This value was 57” less than that above.
|
Location |
Longitude, DMS |
||
|
East entrance to the Glenelg – Tyers’ triangulation |
141 |
00 |
28 |
|
Henty’s Flag Staff – Tyers’ triangulation |
141 |
37 |
57 |
|
Longitude difference |
0 |
37 |
29 |
|
Henty’s House (Flag Staff) – Stokes |
9 |
36 |
22 |
|
Longitude difference Sydney-mouth of Glenelg |
10 |
13 |
51 |
|
|
|
|
|
|
East entrance to the Glenelg – Tyers’ triangulation |
141 |
00 |
28 |
|
Batmans Hill, mean adopted |
144 |
59 |
10 |
|
Longitude difference |
3 |
58 |
42 |
|
Longitude Melbourne-Sydney by Stokes |
6 |
16 |
17 |
|
Longitude difference Sydney-mouth of Glenelg (a) |
10 |
14 |
59 |
|
|
|
|
|
|
Glenelg Sand Hill – Stanley checking Tyers |
141 |
02 |
21 |
|
East entrance to the Glenelg for Stanley |
141 |
01 |
25 |
|
Batmans Hill, mean adopted |
144 |
59 |
10 |
|
Longitude difference from Stanley |
3 |
57 |
45 |
|
Longitude Melbourne-Sydney by Stokes |
6 |
16 |
17 |
|
Longitude difference Sydney-mouth of Glenelg (b) |
10 |
14 |
02 |
|
|
|
|
|
|
Difference Stokes (b) to Tyers (a) |
00 |
00 |
57 |
|
|
|
|
|
|
Longitude Sydney, by Stokes |
151 |
16 |
00 |
|
Longitude difference Sydney-mouth of Glenelg-Stokes |
10 |
13 |
51 |
|
Entrance to the Glenelg – Stokes |
141 |
02 |
09 |
|
|
|
|
|
|
East point, entrance to the Glenelg – Tyers’ mean |
141 |
01 |
23 |
|
Entrance to the Glenelg – Stokes |
141 |
02 |
09 |
|
Difference Stokes to Tyers |
0 |
0 |
46 |
Stokes concluded that as his and Tyers’ differences in longitude between Sydney and the mouth of the Glenelg were within a few seconds of arc, that Tyers’ difference using triangulation should be adopted. He then stated his view that the longitude of Sydney of 151° 16’ was within one minute of the true value and that his value should be used. As can be seen in the table above Stokes’ longitude for the mouth of the Glenelg was 141° 2’ 9” being some 46 seconds of arc further west of Tyers’ location and stating that it was in New South Wales territory which would have continued to please the New South Wales administration.
Now with Stoke’s independent confirmation that Tyers’ Line was indeed too far east, please refer to the table below, there came momentum to resolve the matter and survey and mark a boundary from the sea to the River Murray.
|
East point, entrance to the River Glenelg |
Longitude, DMS |
Distance inside New South Wales, Miles (Miles & links) [Kilometres] |
||
|
Derived by Tyers, 1839 |
141 |
01 |
23 |
1¼ miles (1 mile 2270 links) [2 kilometres] |
|
141 |
01 |
39 |
1½ miles (1 mile 4250 links) [2.4 kilometres] |
|
|
Derived by Stokes, 1842 |
141 |
02 |
09 |
2 miles (2 miles 0 links) [3.2 kilometres] |
A critical examination of these values by the then Imperial authorities resolved that a higher weight be placed on Tyers’ work due to his triangulation. The longitude adopted was that derived by Stanley on his check of Tyers’ work being 141° 2’ 35” being for the longitude of the Glenelg Sand Hill. This now meant that the boundary was no longer 1¼ miles west of the river entrance but 1 mile 4250 links (just over 1½ miles) west. (In the later proclamation of the boundary established by Wade and White, it is stated the boundary as agreed upon commenced at a point 1 mile 4250 links west from the mouth of the River Glenelg).
The 1847-1850 line by Wade and White or Wade’s Line
Surveyor Henry Wade and South Australian government surveyor Edward Riggs White met at the mouth of the Glenelg in 1847. Prior to his leaving Sydney, Wade had been instructed that with only a few seconds of difference between the longitudes of Stokes and Tyers/Stanley for the position of the Glenelg, the mean longitude from their work was to be used for calculating the position of the 141st meridian of east longitude.
By March 1847, Wade had found Tyers’ Arrow and his peg on the north bank of the Basin, but had not received the information on Stoke’s longitude. He thus recorded that he would use the mean longitude from Stanley’s check of Tyers’ work being 141° 2’ 35” meaning that the meridian would be 2 miles 28 chains to the west at then 38° 4’ 18” south latitude (the fact that the longitude 141° 2’ 35” referred to the Glenelg Sand Hill and not Tyers’ Arrow and Line seems to have been overlooked for now, as mentioned above). In hindsight, using the mean would have meant the boundary being moved even further west so perhaps it was fortuitous that Wade commenced work without knowing Stokes‘ value.
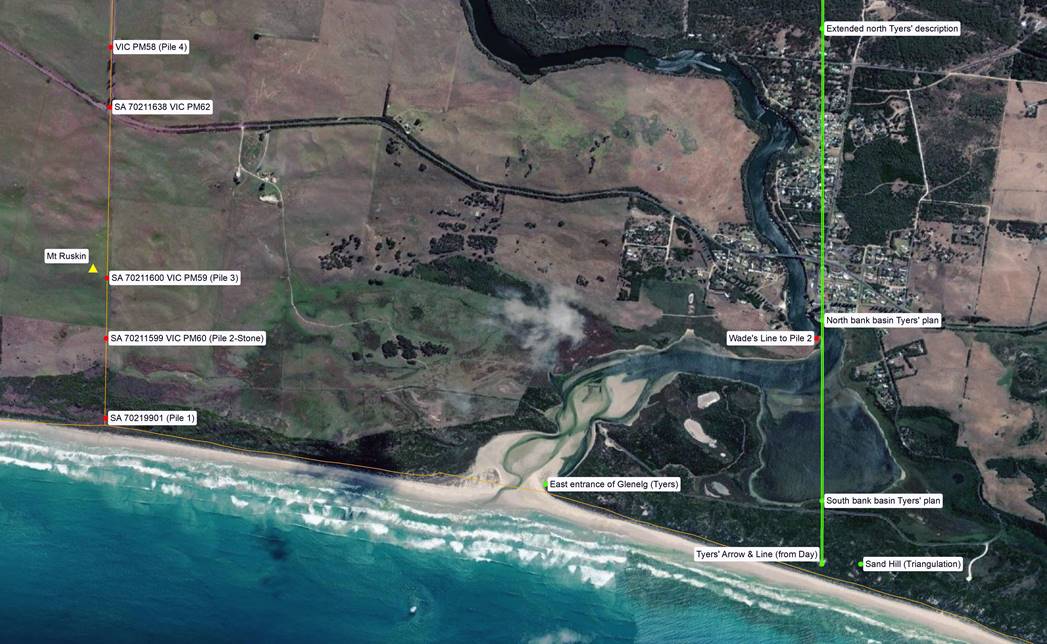
As can be seen in the map below to avoid having to chain across the Glenelg, Wade chose a point on the west bank near where Tyers’ Line passed a little to the eastward of the west point of the inner entrance to the Glenelg (or its entrance from the basin). It was reported in 1895 that Wade determined that from his point on the west bank Tyers’ Line would have been some sixty links east, thus he reduced his distance to be chained from 2 miles 28 chains to 2 miles 27.40 chains. Later, however, the reduction is reported to be only 50 links. It is probable that that Wade allowed some 50 links for the offset to Tyers’ Line plus of the order of 10 links for rounding to the nearest 10 links, totalling 60 links.
As there is some confusion about Wade’s distance measurement it will be accepted for now and discussed in the section on Day’s survey where the information can be more clearly related.
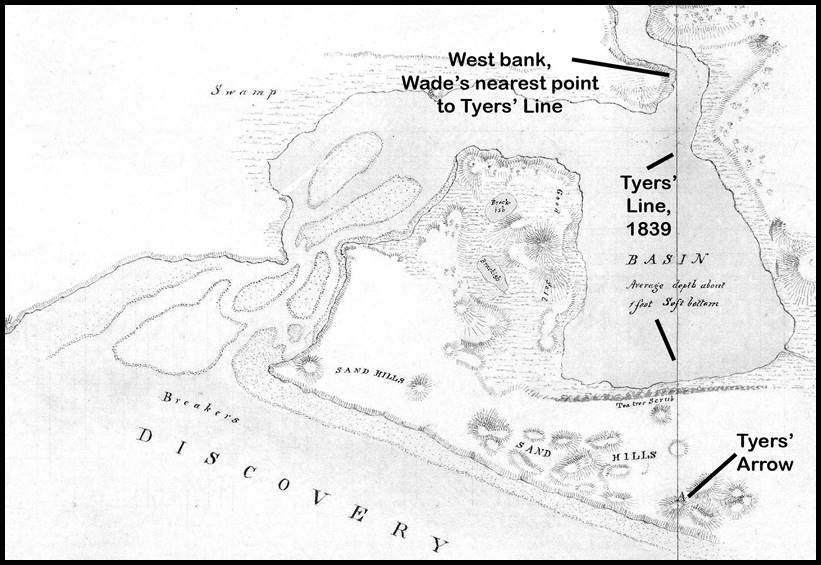
Section of 1839 map Survey of the Lower part of the River Glenelg, showing relative locations of points described herein,
courtesy Public Record Office Victoria : 1839 VPRS 8168/P0002, GLENELG4C2; GLENELG RIVER; TYERS.
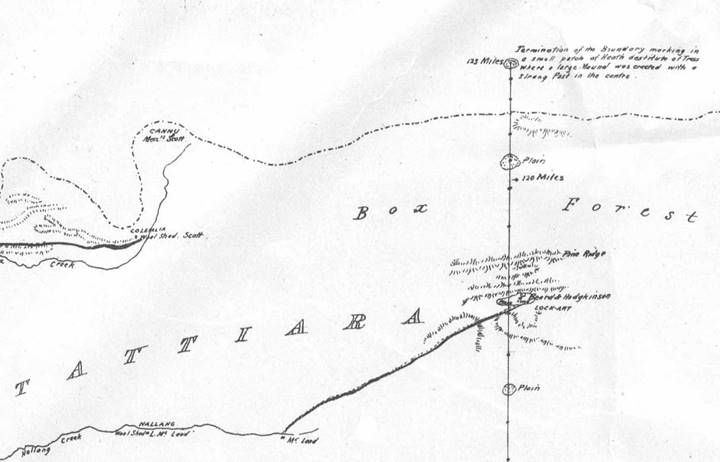
At Wade’s distance west of Tyers’ Line a Mound was erected. Further Mounds of stone and earth and sometimes referred to as Piles or Cairns, were erected 2590 links due south being 375 links north of the coast and 19 chains north of the first on a limestone ridge. From south to north they became Mounds/Piles 1, 2 and 3 with later named Mount Ruskin just to the northwest of Mound 3 (from other survey information Mound/Pile 4 was some 72 chains north of Pile 3). Documented below is the fact that Mound 2 was made of stone. The end of Wade’s surveyed line, some 123 miles from the sea was in latitude 36° 13' 23" south, near today’s Bordertown. Here he erected a large earthen Mound surrounding a strong post which he called Termination Mound. A copy of the 1848 Plan of the boundary line which divides the colony of New South Wales from that of South Australia, by Henry Wade, Surveyor was held by the National Library Australia. Due to the size of the plan only the relevant top and bottom sections are shown below. The bottom section of Wade’s plan has been annotated to show the Mounds and the approximate position of Tyers’ Line.
|
|
|
Bottom section of Wade’s plan edited and annotated to show Mounds 1, 2, 3, and 4 and the approximate position of Tyers’ Line. |
|
|
|
Top section of Wade’s plan edited to show Termination Mound at 123 miles. |
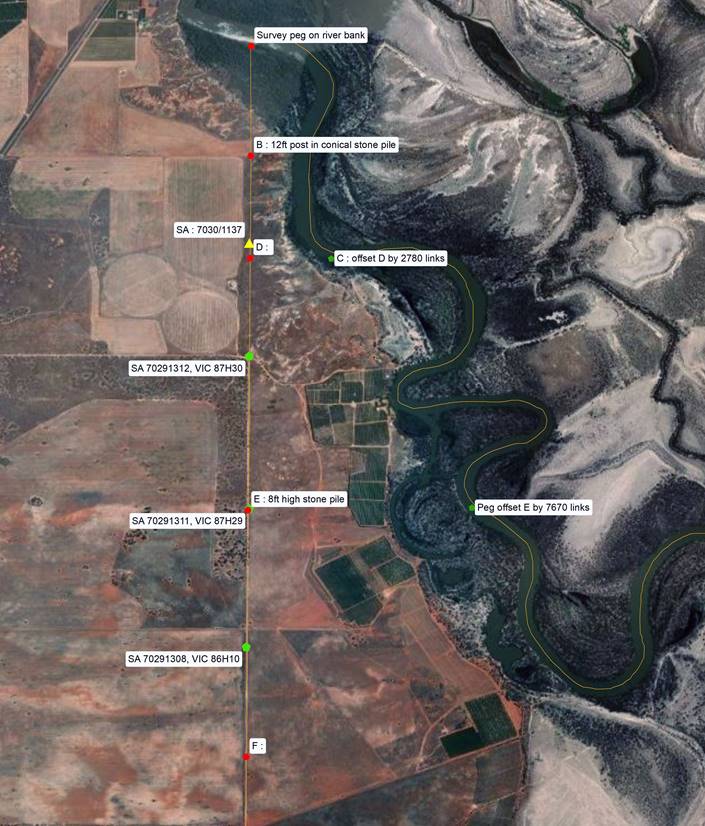
White continued the line to a point 206.5 miles from the coast where the prevailing drought conditions halted the work in 1849. Returning in 1850, the line reached the River Murray some 279 miles (450 kilometres) from the coast. At this northern end of the line White carried extensive surveys to connect his survey line to nearby topography and existing surveys. Due to its size, White’s plan may be viewed via this link and his plot of his connections is shown below.

As shown in the image above of White’s December 1850 Rough Plot of the connection of the South Australian Boundary line with the Surveys of the Murray River, White noted :
|
A |
Peg driven on the line on the New South Wales bank of the River from which one gum-tree marked 141° bears N54°E, 22 links and another marked W bears N199°E, 17 links |
|
B |
Conical pile of Stones with strong post in centre 12 feet high, 47 chains 50 links from River (North) |
|
C |
Peg left by Mr Prichard having a gum-tree marked P bearing N357° 30’E, 35 links [A plan of Osgood Pritchard’s survey including White’s connections may be viewed via this link.] |
|
D |
1 mile 11 chains 75 links South of River |
|
E |
Pile of Stones 8 feet high at road side 2 miles 39 chains 50 links South from River |
|
F |
5 miles 67 chains 50 links South from River |
|
(From F above) True East 5 miles 76 chains (intersection with line) True South 1 mile 38 chains from west bank of Junction of Chowella (Chowilla) Creek |
|
Below are images of the two stone mounds (cairns) noted by White, which are referenced in the Papers.
|
|
|
|
|
White’s pile of stones c1900s (taking the personal height of the observer and the shape of the pile, it appears to be conical and able to hold the pole lying in the foreground (12 feet high centre post). |
Remains of White’s conical pile of stones (originally supporting a 12 feet high centre post). |
Restored stone (8 feet) pile originally by White. |
Todd in his report in the Papers, recorded that the line was run from the coast (38° 4' 3" south latitude at high water mark) to the Tatiara, or to about 36° south, in 1846-7, and continued to the Murray in 1849-50, a conical pile of stones, eight feet high, being built about 2½ miles south of where the line strikes the river, and another pile twelve feet high, on the most elevated ground, forty-seven chains fifty links south of the river. This line was proclaimed in the [South Australian] Government Gazette of 23rd December 1847 where it unambiguously stated that the line delineated on the public maps deposited at the Survey Office, at Adelaide, as the meridian of the one hundred and forty-first degree of east longitude, is and shall be deemed and construed to be the eastern boundary of the Province of South Australia, to all intents and purposes. Elsewhere it maybe said that because White had not completed his survey the border, or at least his section, remains unproclaimed. White’s survey was indeed delineated on public maps of the Survey Office clearly stating it represented the survey of the 141st meridian, hence retrospectively being proclaimed. This conclusion is borne out by the later High Court’s decision in recognising that the boundary marked by Wade and completed by White, represented the position of the 141st meridian as ascertained and marked by the British Government for the purpose of fixing the eastern boundary of the Province of South Australia.
The New South Wales Government Gazette of 2nd March 1849 issued a similar proclamation. Notably, the schedule accompanying both proclamations stated that the boundary as agreed upon commenced at a point 1 mile 4250 links west from the mouth of the River Glenelg, and that at a point 2965 links from the coast a pile of stones (Mound 2 above at 2590 plus 375 links from the coast) had been built; that the line was shown by a double row of blazed trees and large mounds of stone and earth. Where no timber existed, the large mounds were intervisible. A large cairn of stones was erected on the southern bank of the Murray. (Note that the that the distance of 1 mile 4250 links west from the mouth of the River Glenelg appears to have been derived from Stanley’s check of Tyers’ observations in 1840 and based on the longitude of the east entrance to the Glenelg being 141° 1’ 39”, as tabled above).
1865 Gazetteer Map of Victoria
The geodetic survey of Victoria under the control of Robert Lewis John Ellery, also Superintendent of the Melbourne Astronomical Observatory, was undertaken between 1858 and 1872. The establishment and observation at the survey’s 209 primary stations was based on sound geodetic principles starting with the Werribee baseline recognised as one of the most accurately measured baselines of the era. When completed the Werribee baseline measured 55 931.65 feet or 17 kilometres. The whole area of the colony of Victoria, with one exception, Ellery observed in 1873, had been triangulated with a primary triangulation almost equal in accuracy to any in the world, from a baseline, which was measured with all the refinement, skill and instrumental means then available. Ellery continued, pressing for two baselines of verification; one on the western boundary of Victoria, and one in Gippsland, to close and verify the triangulation. The end of the Victorian triangulation came without either baseline being established, which would have been a great disappointment to Ellery, for there was no independent check on the work of his department. The quality of the Victorian triangulation was thus only revealed in the 1930s.
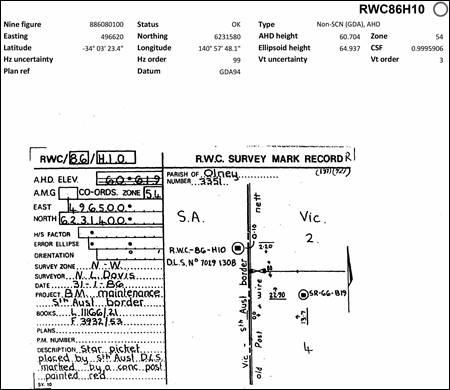
As mentioned above, as part of this survey Surveyor Allan’s work included survey stations that would later enable the South Australian and Victorian geodetic networks to be connected. One of those stations, Mount Ruskin, was occupied as early as 1859 as part of the Victorian survey. When occupying Mt Ruskin near Wade’s Line in May 1865 Allan connected his survey to Wade’s Mounds. An example of such connections was shown on this Diagram being No. 10 of the set of the triangulation of Victoria. It was notable that the connection from Mt Ruskin to Boundary Pile No 3 was stated as 301.000 feet on an azimuth of 131° 50’ 2’ which computes to the boundary being due east of Mt Ruskin by 340 links. Later, TE Day in 1911 gave the same offset as 346 links.
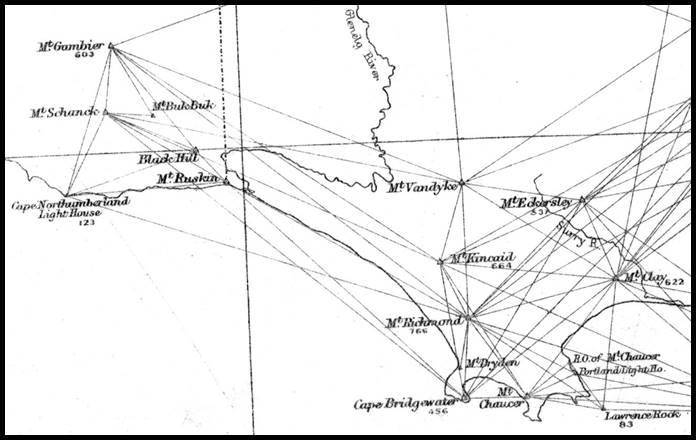
showing the work around the border and Mount Ruskin,
the complete map may be viewed at http://handle.slv.vic.gov.au/10381/120066 , State Library of Victoria.
Enough work on the Victorian geodetic survey must have been completed, however, for the then Surveyor General to permit the 1865 map titled Gazetteer Map of Victoria, to be published. Of note was the fact that the map depicted two lines one of which was described as 141st meridian as defined by Mr Edward White, and marked on the ground, the other as Boundary between Victoria and South Australia being the 141st meridian as adopted by Arrowsmith.

1865 Gazetteer Map of Victoria, printed by permission of Charles Whybrow Ligar, Esqre., Surveyor General; transferred from original stone by William Collis; lithographed at the Department of Lands & Survey, March 31st 1865, courtesy https://nla.gov.au/nla.obj-231377452/view
In the Papers, a Memorandum of 8 March 1870 and plan, as shown below, was included. The Memorandum stated that :
The geographical position of the boundary line between South Australia and Victoria, which was marked in 1847 and proclaimed in the South Australian Government Gazette, 23rd December 1847, has now become known with as much accuracy as the geographical position of the Melbourne Observatory by means of the primary triangulation of the geodetic survey, but is subject to further correction at any time if, by any improved means, the geographical position of Melbourne can be ascertained within closer limits.
The position of the boundary line marked and proclaimed in 1847 is 140° 58' 07.3", and every precaution, possible at the time, appears to have been taken to obtain the position of the 141st meridian correctly; yet the difference between the marked line and the 141st meridian, as determined by the geodetic survey, amounts to 136.63 chains, showing the line to be that distance west of the 141st meridian as obtained by reference to the Melbourne Observatory. (Based on the offset of 340 links from the plan above, Mt Ruskin would have then been in longitude 140° 58' 04.5"). Mt Ruskin was also mentioned as being in longitude 140° 57' 48" from Adelaide and 140° 58' 00" from Melbourne. TE Day’s 1911 plan, please see below, shows the longitude for Mt Ruskin as 140° 57' 56".

Map of Survey of the lower part of the River Glenelg, Department of Crown Lands and Survey, Victoria, circa 1870,
courtesy https://nla.gov.au/nla.obj-232197410/view
Longitude by (Electric) Telegraph
The electric telegraph was a communication system that enabled a message to be transmitted via electric signals over wire from location to location (the signals were either voltaic or galvanic referring as to how the electric current was generated). As there were other telegraphic systems, flags and semaphore for example, still in existence the word telegraph was preceded by electric to be clear about the method used. As the other telegraphic methods became obsolete the word electric was dropped and the word telegraph implied its use of electric current.
Samuel Morse invented a telegraph system that was a practical and commercial success. Morse’s system was first demonstrated in public in 1838 but it was another five years before the American Congress funded the construction of an experimental telegraph line from Washington to Baltimore, a distance of 65 kilometres. On May 1, 1844, this line was first used to dispatch news. The completed line was officially opened on May 24, 1844.
A couple of weeks later, in June 1844, Charles Wilkes (1798-1877) used the telegraph line to establish the longitude of Baltimore. (Wilkes was a Commander in the US Navy and also explorer who in 1838 had led the US Exploring Expedition that discovered inter alia the continent of Antarctica). Unfortunately, the procedure was flawed in that it required human estimation of the fraction of the second. The star signal method was first used in 1846. The difference in longitude between two stations, connected by telegraph, came from measuring the time difference between agreed star(s) crossing the meridian (line of longitude) of the eastern station and then the meridian of the western station. With the advancement of the observational telescopes as many as nine vertical wires within the optics meant that each star could provide up to nine separate crossing times at each location. A clock at one station only was used to record the instance of the star(s) crossing(s). The elegance of the star signal method was that errors in the star's position, as given in the star tables were irrelevant, as were any absolute errors of the clocks as only a single clock was employed. This clock, however, needed to be able to correctly measure the interval between meridian passages at the two stations.
To further remove human error from this methodology a chronograph with paper tape recorder was later used. The chronograph not only accurately maintained time but during observations at each beat (tick) of the chronograph a mark would be automatically made on a roll of paper tape. The observers’ watching for the star(s) passage could also mark the tape at the instant of crossing via telegraph. Very accurate interpolation of the observers’ marks against the seconds’ marks on the paper tape gave the time of passage.
|
|
|
|
Chronograph with paper tape recording (left) and (right) the Sydney Observatory Chronograph also with paper tape recording. |
|
Longitude by telegraph became an acceptable and accurate method of obtaining longitude as it allowed time differences to be measured with greater accuracy (averaged to less than 1/100th of as second) over any distance spanned by the telegraph. It also meant that provided a remote observer had access to the telegraph, longitude difference could be obtained rather efficiently. Purists would argue that a single chronograph would not allow for a correction to be applied for the non-negligible signal travel time. This correction, however, could be obtained from averages of signal time travel found during other two chronograph observations. This was the technology and methodology supporting the work of Todd, Smalley and Ellery in 1868.
1868 Boundary Determination by Telegraph
Following the publication of the 1865 Victorian map depicting an ongoing discrepancy with the border location, its automatic elongation across the River Murray to form the boundary between New South Wales and South Australia, while easy could not be accepted while uncertainty existed. The governments of the affected states (South Australia, New South Wales, and Victoria) in 1868 required the position of the 141st meridian to be re-determined and that their representatives Charles Todd (Superintendent of Telegraphs, SA), George Roberts Smalley (Government Astronomer, NSW), and Robert Lewis John Ellery (Government Astronomer, Vic) to organise the work required.
The Papers show that Todd went to Sydney in March 1868 to confer with Smalley. The two agreed :
|
First |
To make, with the co-operation of Ellery, a careful determination of the difference of longitude between the observatories at Sydney and Melbourne by means of the telegraph.
|
|
Second |
To adopt as an assumed longitude of the Sydney Observatory from which the boundary line should be measured, viz., the arithmetical mean of the longitude deduced from the present assumed longitude of Melbourne, the difference of longitudes having been ascertained, and that adduced by Mr EJ Stone, First Assistant Astronomer at the Royal Observatory, Greenwich, from observations of the moon at Sydney in 1859-60.
|
|
Third |
That the personal equations between the different observers should be determined, Todd observing, for that purpose, with Messrs. Smalley and Russell, at Sydney, and with Messrs. Ellery and White, at Melbourne.
|
|
Fourth |
That Todd should then proceed to the boundary and erect a transit instrument on the north of the river, near to the line of the telegraph connecting Adelaide and Sydney, the wires being brought into the temporary observatory, and that its longitude should be determined :
(a) by signals exchanged with Sydney on two or more clear nights. The signals to be transits over the meridian, or rather over the several wires of the telescope, of certain stars, previously selected, observed at both places, and recorded on the Sydney chronograph, and (b) by signals exchanged in the same way with the Melbourne Observatory on two or more clear nights. The transits being recorded on the Melbourne chronograph. (It was noted that there would be no chronograph at Todd’s temporary observatory near the boundary).
|
|
Fifth |
That the geographical latitude of the transit instrument should then be ascertained by transits of stars over the prime vertical.
|
|
Sixth |
That the longitude and latitude of the transit instrument having been determined and its distance, east or west, from the 141st meridian mutually agreed to, that distance to be carefully chained, and the boundary line so ascertained to be properly marked and run for a short length for the guidance of the surveyors. A post to be set up on the site of the transit instrument for future reference.
|
The first observations were undertaken on 3 April 1868 with the Melbourne and Sydney Observatories being directly connected by telegraph. In the observations that followed between five and nine wires were used with seven being generally noted in the records. The transits of fifteen preselected stars, were observed on both meridians and recorded on the Melbourne chronograph, Messrs. Smalley, Todd, and Russell, observing, in turn, at Sydney, and Mr. White, at Melbourne. The signals transmitted from Sydney were received by a repeater at Melbourne, the armature of which automatically repeated them to the chronograph. From several trials, Ellery had found that the time lost in repeating was 0.027 seconds which was consequently subtracted from the time by the Melbourne clock for each Sydney transit to obtain the true interval. To eliminate the time occupied in the transmission of the signals between the two observatories, the Melbourne clock was made to transmit its beats automatically to the Sydney chronograph, where they were compared with its transit clock. The transits were all reduced to one observer via the personal equations. These observations also allowed for the transit time of the signals to be determined giving a velocity of 11 250 miles (about 18 000 kilometres) per second. The difference in longitude between the observatories of Melbourne and Sydney was found to be 24 minutes 55.81 seconds (6° 13’ 57.15”).
|
Location |
HMS |
DMS |
||||
|
Accepted longitude Melbourne |
9 |
39 |
54.80 |
144 |
58 |
42.00 |
|
Longitude difference Melbourne-Sydney |
0 |
24 |
55.81 |
6 |
13 |
57.15 |
|
Sydney longitude based on Melbourne |
10 |
04 |
50.61 |
151 |
12 |
39.15 |
|
Longitude of Sydney by Mr Stone |
10 |
04 |
47.32 |
151 |
11 |
49.80 |
|
Adopted longitude Sydney - mean |
10 |
04 |
48.97 |
151 |
12 |
14.55 |
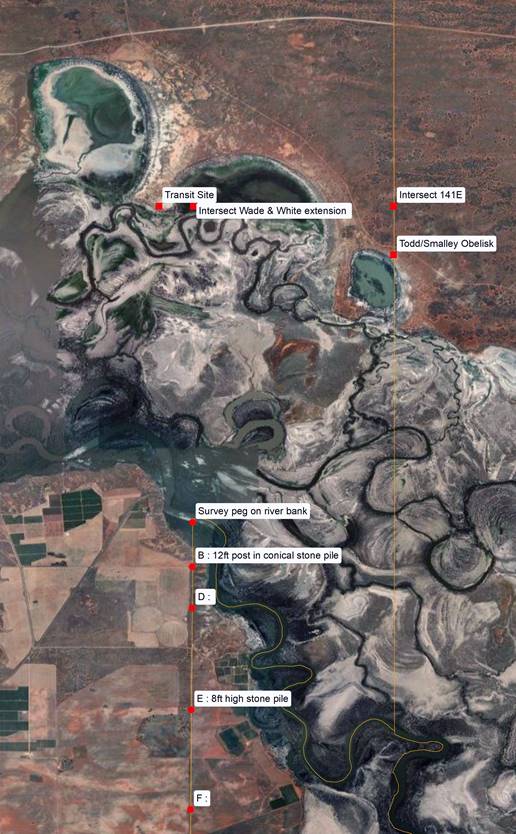
Todd then went back to Adelaide via Melbourne visiting Ellery and White on the way. Then accompanied by Arthur Bevan Cooper (1840-1874), Deputy Surveyor General, South Australia, travelled by River Murray steamer Prince Alfred from Blanchetown to Chowilla. Then presumably using the track now approximated by the Wentworth Road from Renmark to Wentworth, travelled to the site of his Temporary Observatory (Transit site), arriving on 2 May 1868.
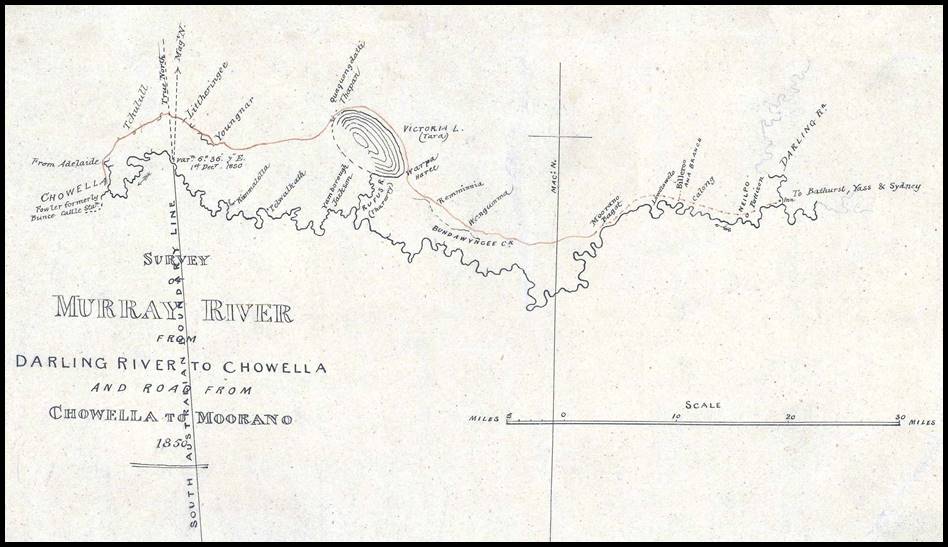
1850s map showing the River Murray with the track between Chowella (Chowilla) and an Inn at the confluence of the River’s Darling and Murray to its north.
Today the town of Wentworth is situated at that confluence.
|
|
|
|
|
Section of Plan shewing produced Victorian Border and part of Boundary between South Australia and New South Wales as fixed by observation of May 1868, as in Papers relating to The Boundary Line Between South Australia and Victoria (Victorian Colonial Government, 1874).
For clarity, the then route of the Adelaide-Sydney telegraph line, meridians and locations of the Temporary Observatory and final Boundary Obelisk have been colour enhanced.
Additionally, below the plan, a Google Earth image of approximately the same region acquired in 2018, indicates the extent of flood plain and dry lakes. |
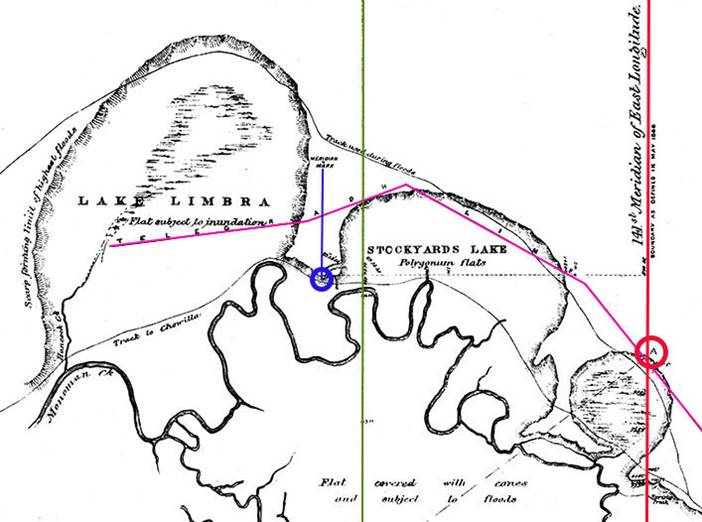
Todd stated that a suitable site for the transit instrument [Temporary Observatory] was found at a distance of 25 chains 56.68 links to the west of the present boundary between South Australia and Victoria, produced north of the river, and about one-third of a mile from the line of electric telegraph, from which a short line of that length was temporarily run up to bring the wires into the observatory. Noting on Todd’s plan above that the present boundary between South Australia and Victoria, produced north of the river was over 4 miles across a flood plain, and there was no time in Todd’s schedule to do such work, the extension had to be done beforehand taking it to the region of the telegraph line. Thus, Todd was able to site his Temporary Observatory (transit) in relation to that line and the telegraph very quickly. Looking at the Google Earth image above the promontory between then Lake Limbra and Stockyards Lake (today only Lake Limbra is depicted in this same region of floodplain) would have made an ideal site being definitively above the floodout even today and overlooking the plains and floodout. As can be seen in Todd’s plan above, the then tracks to Wentworth ran across the flood plain when possible as the shorter route. When this route was impassable a more northerly route on higher ground had to be taken. The telegraph line in the region ran approximately mid way between the two tracks.
Having fixed his instrument site, Todd would then have established the meridian through the transit setting the meridian mark at some 7 chains north of the observatory site, as shown on his plan above. The meridian mark would have allowed him to maintain the consistent alignment of his instrument throughout his observing programs.
On the nights of 9 and 10 May, with clear skies, observations were undertaken in association with the Sydney Observatory. However, Todd noted that the circuit (about 900 miles long) was not very good, and many of the boundary transits could not be recorded on the Sydney chronograph, the adjustment [of the telegraphic system] being difficult, especially on Sunday night. A total of twenty-one zenith stars were observed nine on the first night and twelve on the second, each star providing some seven times of crossing.
On 13 and 14 May, signals were successfully exchanged between the boundary and Melbourne. Over these two nights Todd had a direct circuit with the Melbourne Observatory, via Deniliquin and Echuca, as all intermediate telegraph offices locked down their keys. Todd stated that the nights were brilliantly clear at both places, and the circuit splendid. A total of ten stars were observed, six on the first night and four on the second, again each star providing some seven times of crossing.
These four sets of observations produced the following results (the hours, minutes and seconds used in the results are converted here to degrees, minutes and seconds for easy comparison).
|
Location |
HMS |
DMS |
||||
|
Adopted longitude Sydney – mean |
10 |
04 |
48.97 |
151 |
12 |
14.55 |
|
Difference longitude - transit and Sydney |
|
40 |
59.72 |
10 |
14 |
55.80 |
|
Longitude of transit by signals with Sydney |
9 |
23 |
49.25 |
140 |
57 |
18.75 |
|
|
|
|
|
|
|
|
|
Difference longitude - transit and Melbourne |
|
16 |
03.77 |
4 |
0 |
56.55 |
|
Difference longitude - Melbourne and Sydney |
|
24 |
55.81 |
6 |
13 |
57.15 |
|
Difference longitude - transit and Sydney |
|
40 |
59.58 |
10 |
14 |
53.70 |
|
Adopted longitude Sydney |
10 |
04 |
48.97 |
151 |
12 |
14.55 |
|
Longitude of transit by signals with Melbourne |
9 |
23 |
49.39 |
140 |
57 |
20.85 |
|
Mean longitude of transit |
9 |
23 |
49.32 |
140 |
57 |
19.80 |
|
Weighted mean on stars observed |
9 |
23 |
49.34 |
140 |
57 |
20.10 |
|
Longitude used in field to fix 141° meridian |
9 |
23 |
49.31 |
140 |
57 |
19.70 |
The longitude computed in the field being 9h 23min 49.31sec for Todd’s location and then used to set out the distance to the 141st meridian was later shown to be within 0.01 seconds of time, when the full analysis summarised above was complete.
At the location of the transit Todd also took observations for latitude finding it being in south latitude 33° 55' 8". Using the meridian marker he then turned an angle of 89° 58’ 30” to fix the bearing of the line east towards the 141st meridian.
The adopted position of the transit instrument was thus fixed at 140° 57' 19.7" east longitude, and 33° 56' 8" south latitude, its distance due west from the 141st meridian computed as 2 miles 4468.2 links (equivalent to 2’ 40.3” of arc from the transit longitude). Smalley, on behalf of the New South Wales Government, telegraphed his acceptance of this result, permitting the some 2½ miles to be chained, first by Coooper then by Todd as a check. The meridian 141° east was then set out at an angle of 89° 58’ from the chained line. The chained line from the transit crossed Wade and White’s Line, as extended north of the River Murray, 2556.68 links east of the observatory and 4 miles 680 links north of the Murray, just to the north of today’s Punkah Creek. The salt lakes, west to east, on Todd’s plan were Lake Limbra, Stockyards Lake and a smaller unnamed lake. Today Lake Limbra is named but Stockyards Lake is now named Gum Flat, and the smaller unnamed lake, today named Lake Littra.
Before leaving the Temporary Observatory site, Todd set a stout post, painted white, on the exact site of the transit instrument, with the following painted in large black letters and figures :
|
Longitude, 140° 57 19.7" East. Latitude, 33° 55' 8" South. |
|
|
On east face : |
^ C. Todd, Observer. |
|
On north face : |
Province Boundary, 2 miles 44 chains 68 links East. |
|
On west face : |
^ (^ for arrow) |
From the intersection of the chained line from the Temporary Observatory with the meridian 141° east, the meridian was carefully extended south for 1 mile 5656 links intersecting the telegraph line from Adelaide to Sydney and Melbourne at 5438 links. Where the meridian intersected the upper and lower tracks to Wentworth, a stout white painted post was planted on each side of the two tracks, lettered on the side facing the track :
|
PROVINCE BOUNDARY |
|
On the east side the letters : N. S. W. ; and on the west side : S. A. |
Smalley then met with Todd at Wentworth in November 1868 and after travelling to the boundary, formally accepted it, as marked on the ground, on behalf of the Government of New South Wales.
Todd, in his report in the Papers, stated that the position of the boundary thus determined from the foregoing observations, and mutually agreed to by Mr Smalley and myself on behalf of our respective Governments, would be defined as a meridian line starting from the river Murray, 2 miles 19 chains due east of the pile of stones on the south bank of the river, marking the north end of the line at present adopted as the common boundary of South Australia and Victoria; as, however, there were no good natural landmarks we thought it better to permanently indicate the exact position of the new boundary line by a brick pyramid, 13 feet 6 inches high and 5 feet 6 inches square at the base, which we erected on the slope of the scarp (see Todd’s plan above) at point A, forming the limit of the Murray floods, and immediately to the north of a circular salt lagoon (dry at the time now Lake Littra), having the words "PROVINCE BOUNDARY" on the north and south faces; N.S.W / G.R. Smalley on the east face, and S.A. / Charles Todd on the west face.

The monument, as described above, erected in 1868 at Lake Littra.
The monument was erected a short distance up the slope of a scarp, about 77 yards from the nearest point of the line of the telegraph, on the north side of the line (from Todd’s plan above the meridian intersected the telegraph line at 5438 links from the chained line, meaning that with 77 yards being 350 links the mark was at 5088 links). The bend of the River Murray, immediately to the east of Slaney's Island, some 3½ miles away was on an astronomical bearing of about 53° west of south; the Salt Creek public house was 2 miles 71 chains away bearing 30° east of south; and Mount Hancock was at a bearing of about 16½° east of south. This link shows a section of an 1881 plan depicting the River Murray in the Wentworth region along with Mount Hancock, the border and noting the location of a Cairn denoting the Boundary; 10ft diam, 9 high (diameter 10 feet and 9 feet high, please refer to the 1900s photograph above).
The Government of South Australia now claimed the strip of land between the 1847 line as laid down by Wade and White and the newly determined 1868 position of the 141st meridian. It was found that the width of the strip varied, as the line was not marked a straight line. Wade's portion of the line ran nearly 1° East of True North at first, then True North for a distance and finally slightly west of north (Todd’s plan shows a deviation of 22’ at White’s stone mound with its 12 foot high centre post). White commenced his section of the line running true north, but it gradually swung from 19' up to 24' west of true north. Thus, in 1895 the strip was defined as being 2 miles 1912.2 links (3 603 metres) west of the line as defined by Todd and at the coast 2 miles 1018 links (3 426 metres), calculated by only allowing 882.5 links for curvature of the meridians.
After a protracted legal dispute lasting more than 75 years it was finally ruled by the Privy Council in 1914 that the line erroneously marked was such to have established that line as the legal boundary between the two States. Pointed out during the legal proceedings was that for more than sixty years New South Wales then Victoria exercised the fullest dominion over the land lying to the East of the line. A great portion of the land has been dealt with by lease and licence to occupy, some has been alienated in fee, municipal rates have been collected, and the electoral franchise has been exercised by the inhabitants in elections under the laws of Victoria, and in federal elections as citizens of Victoria.
Local use of the telegraph for establishing longitude was about to be expanded into a global setting. A submarine telegraphic cable was brought ashore at Darwin in late 1871 connecting Australia to the northern hemisphere via Singapore. It was the completion of the Overland Telegraph (the Port Augusta to Port Darwin telegraph line), however, on 22 August 1872 that really ended Australia’s isolation from the northern hemisphere. By 1877 all capital cities except Perth were telegraphically interconnected with Perth’s isolation ending in 1889. Following an arrangement made between the British and Australian authorities in 1882 the longitude chain Greenwich-Australia by the telegraphic method, was completed. These operations resulted in the meridian of Port Darwin (later Darwin) then becoming the origin of Australian longitudes and the following results were obtained and adopted at the time :
|
1883 Longitude |
Hours |
Minutes |
Seconds |
Degrees |
Minutes |
Seconds |
|
Port Darwin |
08 |
43 |
22.49 |
130 |
50 |
37.4 |
|
Adelaide Observatory |
09 |
14 |
20.30 |
138 |
35 |
04.5 |
|
Melbourne Observatory |
09 |
39 |
54.14 |
144 |
58 |
32.1 |
|
Sydney Observatory |
10 |
04 |
49.54 |
151 |
12 |
23.1 |
|
Hobart |
09 |
49 |
19.80 |
147 |
19 |
57.0 |
A global telegraphic circuit was completed in 1902 with a submarine telegraph cable across the Pacific Ocean between Canada and Australia. Canadian Astronomers were keen to close a complete longitude circuit round the earth and by 1903 Otto Klotz of the Dominion Observatory Ottawa, Canada had concluded the necessary work. Despite the close agreement in longitude obtained by Klotz, because of the numerous variables in equipment, procedures, and signal quality his results were only ever considered to be of interest, and existing longitudes were reliable. Additionally, broadcast time was now in its infancy and this new technology appeared to offer a better way forward.
South Australian Government Surveyor Theodore Ernest Day (1866-1943), undertook the survey for the disputed boundary case. Finding the remains of Tyers’ Arrow and about 1 mile of Tyers’ Line northwards he stated that the line ran some 39’ east of north. Day was able to undertake a survey connection between Tyers’ Arrow and Mt Ruskin and from Mt Ruskin connect to Wade’s Line, as shown in his survey plan below. Based on the then longitude of Mt Ruskin (140° 57' 56") he established that Tyers’ Arrow had a longitude of 141° 00' 26" (Mt Ruskin’s longitude plus 2’ 30” from his survey) and that the boundary was 1 mile 6714 links (Mt Ruskin’s longitude plus his offset to Wade’s Line from his survey less 141° being 2’ 01.1”) west of the 141st Meridian. Clearly, Tyers’ survey work was essentially flawless and with the right longitude of Sydney he would have got the right result first time!

Annotated plan of TE Day’s 1911 survey.

The remains of Mound/Pile 3, with its witness posts, on the lower slopes of Mount Ruskin.
The odd shaped strip, defined by Todd above, as a meridian line starting from the River Murray, 2 miles 19 chains (1912.2 links) due east of the pile of stones on the south bank of the river, and at the coast 1 mile 6714 links (2 960 metres) wide (the pile of stones refers to White’s conical pile originally supporting a 12 feet long centre pole). At the River Murray, the GDA94 relativity between the meridian through pile of stones and meridian through the Todd/Smalley Obelisk is 2 miles 1932.6 links. In area, this strip was initially stated as some 332 800 acres (520 square miles, 1 347 square kilometres). Today the estimates say that the area is nearer 350 000 acres (1 420 square kilometres). The table below shows the variation, in decimals of a minute, for GDA94 longitudes for known points of Wade & White
|
Variation in GDA94 longitudes for known points of Wade & White |
||
|
Mound/Pile/Cairn |
Indicative Latitude |
Longitude 140° |
|
Mound/Pile 1 |
-38° |
57.952’ |
|
Mound/Pile 2-Stone |
-38° |
57.953’ |
|
Mound/Pile 3 |
-38° |
57.957’ |
|
Mound/Pile 4 |
-38° |
57.970’ |
|
Termination Mound (supplied, unsubstantiated GPS reading) |
-36° |
57.992’ |
|
White's E : 8ft stone Pile/Cairn |
-34° |
57.810’ |
|
White's B : conical 12ft stone Pile/Cairn |
-34° |
57.823’ |
Wade and White’s Chaining Clarified
In Curnow’s September 1984 article The Boundaries of Victoria, on page 199 of The Australian Surveyor, he wrote as shown in the image of his text below.

The distance of 188 chains (2 mile 28 chains) as used by Wade and White and described above is correct. Unfortunately, Curnow’s figures to deduce it have become confused. Tyers' longitude determinations by chronometer and triangulation as computed by Captain Stanley was 141° 02' 35" as reported above, not Curnow’s 141° 02' 03". Using a sphere for ease of computation Curnow’s longitude differences are evaluated as listed in the table below.
|
Terrestrial Latitude |
Distance Chains |
Distance metres |
|
|
2’ 03” |
Equator |
188.86 |
3 799.160 |
|
2’ 03” |
-38 South |
148.82 |
2 993.779 |
|
2’ 02” |
Equator |
184.25 |
3 706.498 |
|
2’ 02” |
-38 South |
147.61 |
2 969.439 |
|
2’ 35” |
Equator |
238.99 |
4 787.559 |
|
2’ 35” |
-38 South |
187.54 |
3 772.649 |
While a longitude difference of 2’ 03” is 188 chains at the equator, a longitude difference of 2’ 35” at latitude 38° south produces the same result as used by Wade. Regrettably, Curnow’s conclusion that Wade and White introduced a blunder of ½ mile is not substantiated using the correct determinations.
In the 21st century another problem with Wade and White’s chaining was documented. As Day’s 1911 survey was the last to provide a distance between Tyers‘ Arrow and Line and Wade and White’s boundary line a close confirmation of Day’s distance was obtained from Victorian survey marks (PMs) at Pile 2 of stone on the boundary (SA 70211599, VIC PM60) and a Victorian survey mark (PM116060122) on the west bank near where Tyers’ Line passed a little to the eastward of the west point of the inner entrance to the Glenelg (or its entrance from the basin). PM116060122 was the best modern survey mark that could be identified as being close to Tyers’ Line. The table below presents the data.
|
Between Locations |
Survey |
Distance links |
Arc Seconds |
|
Mt Ruskin – Wade & White 1847 Boundary |
Victorian Geodetic, c1865 Day, 1911 GDA94 |
340 346 350 |
3 3 3 |
|
Mt Ruskin – Tyers’ Arrow |
Day, 1911 |
18 213 |
150 |
|
Wade & White 1847 Boundary – Tyers’ Arrow (computed from Day’s 18 213-346 links) |
Day, 1911 |
17 867 |
147 |
|
SA 70211599, VIC PM60 - VIC PM116060122 (computed to provide indicative check on Day’s 1911 distance) |
GDA94 |
17 707 |
146 |
|
|
|
|
|
|
Wade’s offset required cited as being 2’ 35” or 2 miles 28 chains west |
Stanley’s check of Tyers, 1840 |
18 800 |
155 |
|
Wade’s offset as found from Day above |
Day, 1911 |
17 867 |
147 |
|
Difference in Wade’s work (computed) |
|
933 |
8 |
|
|
|
|
|
|
Tyers’ Arrow - Glenelg Sand Hill (cited as separated by 10 chains (1 000 links) in one case and 200 yards (909 links) in another |
Tyers, 1839 |
955 (mean 1000 & 909 |
8 |
|
|
|
|
|
|
Glenelg Sand Hill – then 141st meridian (cited as being 2’ 35” or 2 miles 28 chains) |
Stanley’s check of Tyers, 1840 |
18 800 |
155 |
The distance (17 707 links) from the modern Victorian survey data supports Day’s 1911 distance of 17 867 links which in turn indicates that rather than chaining 18 800 links (2 miles 28 chains) Wade was short by 933 links (18 800-17 867 links). On such an important survey, over such a relatively short distance, could such an error have been made?
From what was reported, Wade saw that the Glenelg was a major obstacle to his chaining west, especially if he started south of the basin in the region of Tyers’ Arrow. Wade is thus recorded as starting his work ascertaining the approximate meridian on the east side of the entrance finding Tyers’ Arrow, not without some effort, and his peg and marked tree on the opposite bank of the basin. This was to enable Wade to connect Tyers’ survey to his own when he moved to the western side of the basin. Tyers’ Line was estimated to pass 50 links to the east of the point on the western side of the river near where the river entered the basin. White is also on record as saying that Tyers’ meridian was ascertained on the east side of the entrance. It is unfortunate that the word entrance is used without qualification as this fact does lead to misinterpreting the record.
One of Tyers’ tasks was fixing the entrance (the east to be precise) of the River Glenelg, so there is much discussion around this issue where entrance refers to that of the River Glenelg and its entrance to the sea. Once Wade & White start their work, however, entrance takes on another meaning and its location is some 1.4 kilometres east of that of Tyers. The entrance described by Wade and White is that of the River Glenelg and its entrance to the Basin of the Glenelg (sometimes just the Basin). Please refer to the map below.
Clearly, Wade did not chain along the coast commencing at Tyers’ Arrow, as recorded elsewhere. If so he could not have avoided chaining across the Glenelg and in any case the distances chained do not fit such circumstances. Wade was able to access the nearest point to Tyers’ Line from the west bank of the River Glenelg near its entrance to the Basin, being a shorter route and completely avoiding the complexity of chaining across the river.
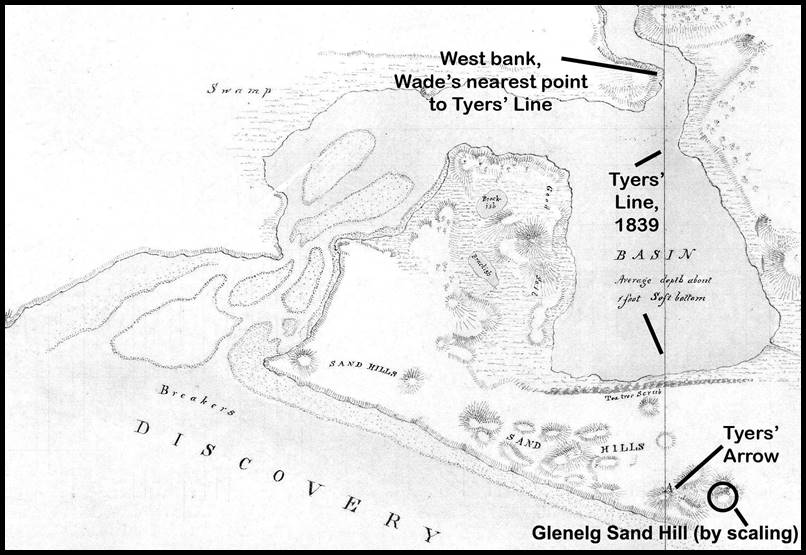
Annotated section of map of Survey of the Lower Part of the River Glenelg copied by Edward Kennedy,
showing the position of Tyers’ Arrow, Line, the Glenelg Sand Hill (approximately) and location on west bank selected by Wade to begin his chaining west.
In addition to establishing the most efficient way to fix the offset to the new meridian from Tyers’ work, it is hard to imagine that Wade had not studied Tyers’ report, for anything that would help him to find the Arrow, once he arrived on site; as the only marked point of reference finding the Arrow was paramount. Thus, while on the east side of the river in the region of Tyers’ Arrow the higher Glenelg Sand Hill, being Tyers’ triangulation point, may have been more prominent in helping finding Tyers’ Arrow 200 yards (being 909 links also quoted as 10 chains) west, as noted by Tyers. Perhaps there or even before, he may have realised that while all the Powers’ discussion about what longitude to adopt, the fact that the adopted longitude of 141° 02' 35" actually referred to the Glenelg Sand Hill and not Tryers’ Arrow and Line. In pursuit of accuracy, whether Wade just accepted Tyers’ distance or checked it himself, noted that the planned distance computed to be chained should be reduced in the order of the lesser 9 chains, to account for the separation of the two locations. Then rather than go into lengthy explanations in his reports he continued to use the agreed 2 mile 28 chains distance as expected by his superiors, whilst chaining 2 miles 19 chains (17 900 links), being comparable with the distance found by Day (17 867 links). It may be coincidence but the latter explanation is plausible, Wade being the man on site and adjusting to the reality of the situation and not what may have been discussed back in the office.
Adopting a Common Datum for the above Surveys
Until the 1960s the geographical separation of the various Australian capital cities and other major centres of settlement, meant that many land surveys started on some suitable local datum. It was only when state based geodetic surveys met at a border region that consistency between the surveys was sought. Reliable relativity between observatories saw standardisation of time/longitude and latitude.
In 1966 Australia had its first national datum the Australian Geodetic Datum (AGD66) based on a best fitting (for the Australian region) mathematical surface the Australian National Spheroid (ANS). The 1966 national adjustment of the Australian Geodetic Survey comprised the raw survey data from some 2 506 survey stations connected by traverse and triangulation networks, converted into a continental wide series of very accurately related coordinates in latitude and longitude. In 1994 the Geodetic Datum of Australia (GDA94) was adopted to conform to an earth centred datum suitable for GPS positioning. Even though Australia now operates with GDA2020 many spatial datasets still have GDA94 coordinates listed without the need for conversion. Thus GDA94 coordinates are used in this further analysis and any map derivation. The means now exited to take the isolated surveys of the surveyors discussed above, and bring them into a uniform relativity no matter what astronomical or terrestrial datum was used.
The Land and Survey Spatial Information (LASSI) website for Victoria and the South Australian Property and Planning Atlas (SAPPA) website were both examined in the coastal and River Murray regions for border survey stations, both recent and historical. In some cases both websites listed the same survey station with its own state identifier and that of the other state. Additionally, mapping, both cadastral and topographic, added their own information. The results are tabled below under the major headings of Coastal and River Murray.
|
COASTAL |
|
|
SA 70219901 (Pile 1) : Described as Stone Cairn and border cairn position re-established, 11/05/1989. |
No helpful diagram. |
|
SA 70211599, VIC PM60 (Pile 2-Stone) : Described as Border Cairn and Victorian PM60 |
No helpful diagram. |
|
SA 70211600, VIC PM59 (Pile 3) : Described as Border Cairn and Victorian PM59, related PM56 notes that at site of PM59 Old Bottle Found. ‘Cairn 3’.
|
|
|
SA 70211638, VIC PM62 : Described as SA-Vic border survey PM Glenelg 62. |
|
|
VIC PM658 : Described as Border Survey Plaque – In Situ In Limestone. |
|
|
River Murray |
|
|
SA 70301137 also T5/7029, VIC 87/H31 : Depicted on NTMS, 7029 Renmark, map sheet. |
|
|
SA 70301136 : Described as Cairn 1901 and by location can only be White’s conical stone pile with centre pole of 12 feet.
|
|
|
SA T3/784 (no record found on websites) : Described as Stone pile on SI5410 Renmark, R502 map sheet and by location can only be White’s stone pile with centre pole of 8 feet (restored pile in photograph).
|
|
|
SA 70291312, VIC 87H30 : Modern mark very close to border.
|
|
|
SA 70291311, VIC 87H29 : Modern mark very close to border.
|
|
|
SA 70291308, VIC 86H10 : Modern mark very close to border.
|
|
|
Additional Coordinates & Computed Values |
|||||||
|
Coastal |
GDA94 Latitude DMS |
GDA94 Longitude DMS |
Comments |
||||
|
Mt Ruskin |
-38 |
2 |
49.27 |
140 |
57 |
54.50 |
Extracted from GDA94 coordinate database |
|
Tyers’ Arrow |
-38 |
3 |
50.10 |
141 |
0 |
24.50 |
Computed from Day’s survey connection to Mt Ruskin |
|
Glenelg Sand Hill |
-38 |
3 |
50.10 |
141 |
0 |
32.20 |
Computed from Tyers’ values in his report |
|
|
|||||||
|
River Murray |
|
|
|
|
|
|
|
|
Todd/Smalley Obelisk |
-33 |
55 |
45.91 |
141 |
0 |
9.91 |
Extracted from GDA94 coordinate database |
|
Transit (Temporary Observatory) |
-33 |
55 |
-- |
140 |
57 |
50 |
Computed from Todd’s survey connection to the Obelisk; latitude is only approximate |
|
SA T3/784 (White’s stone pile with centre pole of 8 feet). |
-34 |
1 |
3.4 |
140 |
57 |
48.6 |
Geodetically computed from White’s survey distances |
A modern, GDA94 coordinate based view of the locations discussed during this review are shown in the table below with links to the full resolution images.
|
|
|
The coastal work of Tyers (right) and Wade and White (left) connected via Day’s survey and showing modern survey marks and their placement with respect to the original mounds/piles/cairns - link. |
|
|
|
The work of White in the River Murray region showing his mounds/piles/cairns and topographic connections and showing modern survey marks and their placement with respect to the original mounds/piles/cairns - link. |
|
|
|
The work of Todd and others in the River Murray region showing his Transit and Obelisk sites plus the mile markers, from the centre of the river, on the extension of the Wade & White boundary north as determined at White’s conical stone mound/pile/cairn – link. |
|
|
|
An overview of the work of White and Todd in the River Murray region showing the relativity of significant points established during their surveys – link. |
The table below illustrates the change in the width of the disputed region over time. Generally 3.35 an 2.96 kilometres are the widths quoted, however, based on how the GDA94 longitudes are calculated the parameters can differ by a few metres.
|
Era |
River |
Coast |
Comments |
||
|
Circa 1900 |
2 miles 1912.2 links |
3 603 meters |
2 miles 1018 links |
3 426 metres |
|
|
Circa 1910 |
2 miles 1912.2 links |
3 603 metres |
1 mile 6714 links |
2 958 metres |
~½ kilometre reduction at coast |
|
2 miles 635 links |
3 346 metres |
1 mile 6908 links |
2 999 metres |
257 metres reduction at river, 41 metres increase at coast |
|
|
GDA94** |
2 miles 660 links |
3 352 metres |
1 mile 6904 links |
2 998 metres |
251 metres reduction at river, 40 metres increase at coast |
|
Notes : (*) Based on Todd’s and Day’s work converted to GDA94. (**) In terms of GDA94 the position of the Todd/Smalley Obelisk is east of the meridian by 242 metres; the distances were computed from the longitude of White’s conical stone pile which had a 12ft centre pole and 141° E and Wade’s Pile 2 (stone) and 141° E. |
|||||
From the 1868 work of Todd, Smalley and Ellery, which saw the Todd/Smalley Obelisk established on the 141st meridian, the shift to the GDA94 coordinate system in this region has been 242 metres eastward. Thus from an academic standpoint the disputed region is now smaller by some 100 square kilometres (some 40 square miles).
What cannot be disputed, however, is that this review has shown that the work of Tyers, Wade and White, Todd, Smalley and Ellery and finally Day used the technology and techniques available to them to achieve the best possible result using the data that was within their control. Had more accurate information been available to them the results would have been different but no less accurate.
South Australian Survey Department surveyors E MacGeorge, Thomas Evans and William Pearson established the boundary north of the Todd/Smalley Obelisk during 1869 and 1870. At the 200 Mile Post Evans took ill and returned to Adelaide. Pearson, now assisted by EA Harris, continued the line to a distance of 348 miles from the River Murray. For some reason, the line extended 2 miles beyond the 29th parallel of latitude, that being the Queensland border. The Government of New South Wales contributed £500 towards the cost of this survey which fixed the boundary between New South Wales and South Australia.
May 1879 saw William Barron, Surveyor from the South Australian Survey Department, proceeded to the intersection of the 141st meridian of longitude with the 29th parallel of latitude, now Cameron Corner, and extend the line north for a further 90 miles. When ill health forced his return to Adelaide, Augustus Poeppel took over and extended the line northwards to the 26th parallel.
When Poeppel reached the vicinity of the 26th parallel, Queensland surveyor, Alexander H Salmond joined him and they jointly established the point today known as Haddon Corner. At this point 552 miles 714 links, some 890 kilometres, from the centre line of the River Murray the 26th Parallel was reportedly fixed to within a ½ arc second, or approximately 15 metres, in distance.
Poeppel then turned west to chain another 186 miles 49 chains to establish the 26th parallel before turning north to complete the South Australian/Queensland boundary at the Gulf of Carpentaria. This, however, was another saga!
Tyers, Charles James (1840), Report of an expedition to ascertain the position of the 141st degree of east longitude being the boundary line between New South Wales & South Australia : by order of His Excellency Sir George Gipps, Knight, &c., &c., &c., Governor and Captain General of New South Wales, Stokes, Sydney.
Victorian Colonial Government (1874), Papers relating to The Boundary Line Between South Australia and Victoria - presented to both Houses of Parliament by his Excellency’s Command, No.92 of 800 printed, John Ferres, Government Printer, Melbourne.
Tyers’ description of his 1939 boundary line at the Basin of the Glenelg
(Tyers, Charles James (1840), Report of an expedition to ascertain the position of the 141st degree of east longitude being the boundary line between New South Wales & South Australia, first published, Sydney, 1840, printed by FM Stokes accessed at : https://catalogue.nla.gov.au/catalog/2499683 )
We commenced measuring a true north line from the spot found to be 35deg 52min of longitude west of Portland Bay by Mr. Townsend’s chain measurement.
From the sea coast it passes ten chains west of a high sandy hillock, (the south and west sides of which are quite bare), over one of the same range not quite so high, (on this we made a hole one foot deep and three long in the shape of a broad arrow, which we filled with limestone) through a hollow then over another hillock, not so high as either of the former.
It then passes through a scrub (Melaleuca) a chain and a half wide, divides the basin nearly into two equal parts, and passes a little to the eastward of the west point of the inner entrance to the Glenelg (or its entrance from the basin) and through a bush on the opposite bank, under which we drove a peg, and marked a tree behind it.(There being no wood of any kind growing near this line, from the beach to the swamp, recourse was had to filling up with limestone, at nearly every chains length, holes of one foot and a half long, by one foot broad, placing a peg by the side of each.)
It then continues three miles seventy-three chains and ninety links through a thick forest, when it cuts the Glenelg nearly at right angles. This part of the line is shewn by marked trees.
From a sand hill two hundred yards east of the marked line, I obtained angles and true bearings to Bridgewater hill, Richmond hill, and Mount Kincaid; by which I was enabled to connect the trigonometrical survey thus far. Having obtained three lunar observations (which gave the longitude of the camp 141° 3’ 8”) determined the rate of the chronometer, and surveyed the lower part of the Glenelg.
Tyers’ plan may be viewed via this link.