The Johnston Geodetic Station / Johnston Origin
Compiled by Paul Wise 2014, revised 2018 and 2023
Introduction
Prior to 1965, a rocky outcrop overlooking Mount Cavenagh Station homestead in the Northern Territory had no particular significance and was only shown as a small brown blob on the map. Even the earlier Nat Map geodetic trigonometrical survey had bypassed this point preferring the higher peak of Mount Cavenagh as the site for a survey station.
Site of the Johnston Geodetic Station; left photograph courtesy August Jenny 2014, right image courtesy Google Earth.
By the middle of 1967 however, this outcrop was marked by a specially constructed rock cairn in which was set a bronze plaque indicating that this point was the Johnston Geodetic Station, also sometimes called the Johnston Origin.
This article explains why an unassuming lump of rock became the first calculated origin and centre of Australia. In addition, before Australia adopted the Australian National Spheroid as its 1966 Figure of the Earth, just a few years before Australia developed another Figure of the Earth, the first to be based on Australian survey and International data.
Background
Until the early 1960s the origin for most of the Australian Geodetic Survey was the coordinates of the Sydney Observatory. However, because other agencies were also involved in completing this national survey task other local origins were also used. A single origin had to be found that was applicable to the whole of the Australian region.
To determine the mathematical surface or spheroid that best fitted the whole Australian landmass or geoid, a central origin near the centre of the continent was required. This point, where the spheroid and geoid intersected, would then locate the centre of the Australian spheroid. With the elements of the spheroid determined all points of the geodetic survey could then be referenced to a consistent datum providing a homogeneous network of horizontal positions.
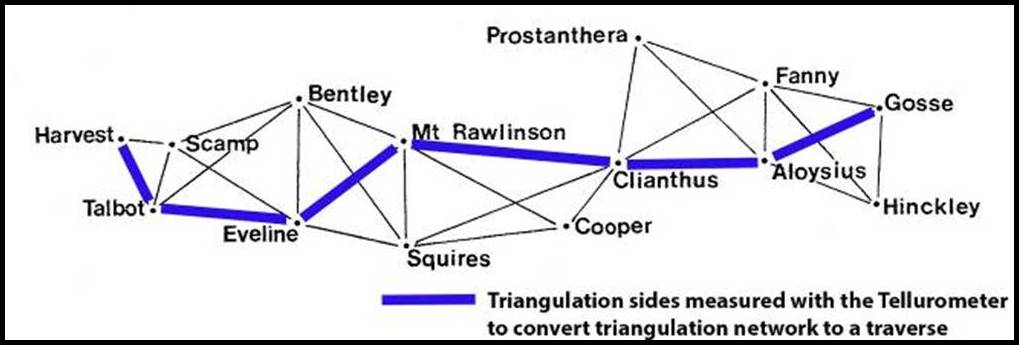
The major loops of the geodetic survey were completed by the end of 1965. In addition, Tasmania and Papua New Guinea also had accurate survey connections to mainland Australia. These loops and connections were all the result of survey traverses of Tellurometer distance and azimuth (direction). However, as triangulation significantly contributed to the geodetic survey, the triangulated sections were converted to traverses. This was achieved by measuring a continuous string of selected triangulation sides through the triangulation network with Tellurometer electronic distance measuring equipment.
Showing how a section of a triangulation network can be converted to a traverse by measuring a continuous string of selected triangulation sides with Tellurometer electronic distance measuring equipment.
An additional program of observations was also undertaken. At selected trigonometrical stations on the geodetic survey, highly accurate astronomical observations were recorded to determine latitude, longitude and azimuth. Such observations used precision theodolites and sophisticated apparatus for time signal reception and time recording. At these so called Laplace stations the difference between the astronomic and geodetic coordinates was thus obtained. When these values were used in the Laplace equation the correction to the observed astronomic azimuth was found and used in the geodetic adjustment to correct the observed survey traverse azimuths. Annexure A describes the Laplace correction in greater detail.
In practical terms the difference between the astronomic and geodetic coordinates is caused by random variations in the Earth's gravity from place to place. These variations mean that the plumb line at a point does not always point towards the centre of the Earth. Lambert in his 1964 paper The Role of Laplace Observations in Geodetic Survey, discussed the use of the Laplace observation in the Australian context.
Further, as detailed by Bomford in his 1964 paper Small Corrections to Astronomic Observations, all Laplace astronomic observations had to be reduced to a common standard. Specifically, this standard involved the following three elements. Firstly, the celestial reference frame for the observed stars had to be as defined in the Fourth Fundamental Katalog (FK4). Secondly, movement of the Pole was as set by the Bureau International de l'Heure Mean Pole of Epoch. Finally, longitudes determined before 1962 were corrected to the Greenwich meridian of 1962.0 which was when new conventional longitudes were adopted to bring the zero of longitude back on to the former meridian of Greenwich as closely as possible. Although these corrections seemed very small in themselves, their cumulative effect could negatively impact the outcome of a national adjustment if the corrections were not applied beforehand.
The Central Origin for an Australian Spheroid
To make the Laplace computations described above, there had to be an interim cohesive set of coordinates for the geodetic survey. As no specific Australian spheroid then existed these coordinates had to be based on a suitable interim spheroid.
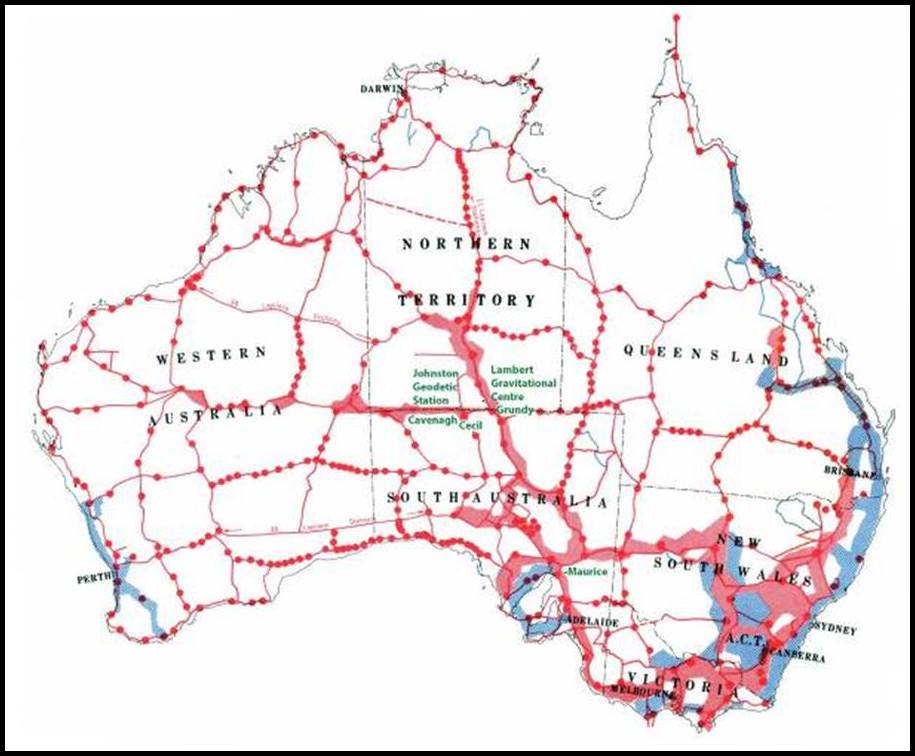
Map showing the Laplace stations (red dots), mainland loops and network of the geodetic survey and places mentioned in the text in green (indicative only).
In his 1962 paper A Figure of the Earth for Australia, then Director of National Mapping, Bruce Phillip Lambert, summarised Australia’s work on defining a Figure of the Earth. The Australian definitions used results from some completed sections of the geodetic survey of Australia combined with international values.
For a short period in 1962, the necessary geodetic computations were performed on the NASA (United States, National Aeronautical and Space Administration, 1971) spheroid, with the central origin being the coordinates of trigonometrical station Maurice. The Maurice origin emerged from the astronomic/geodetic comparison of the coordinates at 54 Laplace stations along the vicinity of the 32º parallel between Sydney and Perth. Trigonometrical station Maurice was on Maurice Hill some 16 kilometres south west of Orroroo, South Australia. Deduced deflections at these 54 stations were also used to derive the best arc radius to fit. From an analysis of 76 Figures of the Earth derived worldwide since 1900, the directly determined value of the semi major (equatorial) axis (a) was 6 378 183 ± 17 metres, while the a value derived by applying a correction for the 1/298.3 flattening to the (polar) b radius, was 6 378 163 ± 13 metres. The mean of these two values (a = 6 378 173 metres) was accepted as the best value obtainable from this approach.
The work of Fischer (1960) and Kaula (1961) was also then integrated. Fischer’s paper gave the results of analyses of geoid undulations over the Americas and over Europe, Africa and Asia by determining the most probable fitting geoid as computed from astro gravimetric deflections and alternatively by matching the astro-geodetic undulations with a series of undulations computed separately from gravimetric data. Kaula derived his Figure from an intensive analysis of gravimetric, astro-geodetic and satellite data. The mean of the four values was found as summarised in the table below.
|
Derived a value (metres) |
Source |
|
6 378 173 |
National Mapping above |
|
6 378 155 |
Fischer (1960) |
|
6 378 160 |
Fischer (1960) |
|
6 378 163 |
Kaula (1961) |
|
6 378 163 |
Mean of above four values |
The mean value was then rounded to the nearest 5 metres, giving the following values for an Australian determination for the best Figure of the Earth :
major equatorial axis (a) = 6 378 165 ± 15 metres;
flattening (f) = 1/298.3.
The Figure defined by the values a = 6 378 165 metres and f = 1/298.3, became known as the 165 spheroid and was used from April 1963 to April 1965. The 165 spheroid’s central origin was based on the astro-geodetic comparison of the coordinates at 155 Laplace stations spread over the whole of Australia with the exception of Cape York and Tasmania.
The coordinates of Maurice as determined by astronomical observation or the spheroid and origin were :
|
165 spheroid, 165 central origin : |
S 32° 51' 13.979", E 138° 30' 34.062" |
|
165 spheroid, Maurice central origin : |
S 32° 51' 13.000", E 138° 30' 34.000" |
|
Clarke 1858 spheroid, Sydney origin : |
S 32° 51' 11.482", E 138° 30' 42.290" |
|
Observed Astronomic : |
S 32° 51' 11.341", E 138° 30' 25.110" |
At their 1964 meeting in Hamburg, the International Astronomical Union (IAU) adopted the values a = 6 378 160 metres and f = 1/298.3. The 1967 Lucerne meeting of the International Union of Geodesy and Geophysics (IUGG) adopted the values a = 6 378 160 metres and f = 298.247167427 for use when a greater degree of accuracy was required. Noting these values in the light of existing Australian work, the Australian National Mapping Council agreed that the parameters, a = 6 378 160 metres and flattening f = 1/298.25 (exactly), were an appropriate fit for Australia and adopted these values for the Australian National Spheroid (ANS) in 1966, and the basis of the Australian Geodetic Datum (AGD) of 1966. Although the ANS was used as the best fit to the Australian regional geoid, its centre did not coincide with the centre of mass of the earth i.e. it was non-geocentric, by some 200 metres.
The major parameters of the various abovementioned spheroids were :
|
Spheroid name |
Semi-major (equatorial) axis (a) metres |
Flattening 1/f |
|
Clarke 1858 |
6 378 293.645 |
294.26 |
|
NASA |
6 378 148.0 |
298.3 |
|
165 (1963) |
6 378 165.0 |
298.3 |
|
IAU (1964) |
6 378 160.0 |
298.3 |
|
IUGG (1967) |
6 378 160.0 |
298.247167427 |
|
ANS (1966) |
6 378 160.0 |
298.25 (exactly) |
Frederick Marshall Johnston, former Commonwealth Surveyor General and the first Director of National Mapping passed away in 1963. The following year the National Mapping Council (that he did much to create) resolved:...that a special geodetic station be established and suitably monumented in the centre of Australia as the origin of the National Geodetic Survey and that this station be named Johnston in memory of Frederick Marshall Johnston former Commonwealth Surveyor General and the first Director of National Mapping.
In May 1965, a complete recomputation of the geodetic survey of Australia commenced, emanating from trigonometrical station Grundy, whose coordinates on both the 165 spheroid and the Australian National Spheroid were 25° 54' 11.078"S and 134° 32' 46.457"E. Trigonometrical station Grundy was on Mount Grundy about 35 kilometres south of Finke in the Northern Territory and 135 kilometres almost due east of the later determined Johnston Geodetic Station. It is now interesting to note that Mount Grundy is less than 50 kilometres south of the Lambert Gravitational Centre that was determined in 1988 and named after Bruce Philip Lambert, the longest serving Director of National Mapping.
By December 1965, further Laplace observations had also been undertaken to then include Cape York and Tasmania, bringing the total number of Australian Laplace stations to 533. Of these Laplace stations, 275 stations were judiciously selected (please refer to figure below) and an astronomic/geodetic comparison of their coordinates revealed that:…random undulations in the geoid [earth’s surface] make it impossible to locate a centre for the spheroid with a standard error of less than 0.5 seconds [of arc], about 15 metres, even with a very large number of stations. This finding saw the central origin calculated using these 275 Laplace stations being adopted as the best available at the time. Thus, as resolved by the National Mapping Council the coordinates of this central origin would determine an area in which the Johnston Geodetic Station, or Johnston Origin, could be located. Its centrality later gave this point notoriety as the first calculated centre of Australia!
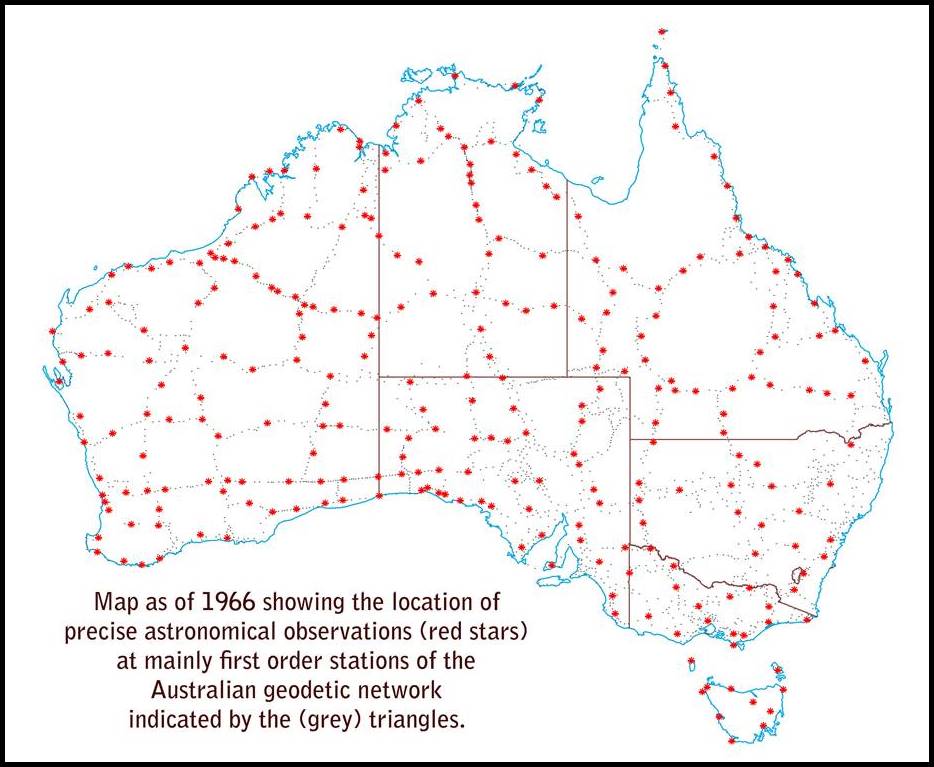
Map showing the distribution of the 275 Laplace stations within the first order geodetic network (after Bomford, 1967).
As described below, the Johnston Geodetic Station was established and constructed on a granite outcrop about one kilometre from Mount Cavenagh homestead. Officers of the Division of National Mapping undertook the task during October and November 1965. First order survey connections were made to the nearest, intervisible, existing trigonometrical stations on Mount Cavenagh and Mount Cecil. The precise coordinates of the origin station once calculated were then used in the final adjustment.
The 1966 national adjustment of the Australian Geodetic Survey comprised some 2,506 stations, 53,000 kilometres of Tellurometer traverse, the geodetic triangulation nets, and 533 Laplace stations. This adjustment was carried out by National Mapping for the National Mapping Council after intensive verification of the input data. Nat Map had access to the Control Data Corporation 3600 computer of the Commonwealth Scientific and Industrial Research Organization (CSIRO) in Canberra. The computer allowed such a volume of raw survey data to be converted into a continental wide series of very accurately related coordinates in latitude and longitude. This adjustment used the ANS with its central origin at the Johnston Geodetic Station, having the three dimensional coordinates of :
|
Latitude: |
25° 56' 54.5515" S |
|
Longitude: |
133° 12' 30.0771" E |
|
Elevation: |
571.2 metres above the Spheroid |
The Australian Geoid
The term geoid is often used to describe the equipotential surface of the Earth; the surface of the Earth's gravity field which best corresponds with mean sea level. In the context of a Figure of the Earth, the spheroid is a mathematical shape that best fits the geoid overall. Owing to variations in the composition and density of the Earth’s crust, differences in mass will cause the geoid to dip below or rise above the surface of the spheroid. In Australia where heights are related to the Australian Height Datum (AHD) the AHD is about 0.5 metres above the geoid in northern Australia and roughly 0.5 metres below the geoid in southern Australia.
Today heights obtained from Global Navigation Satellite System (GNSS) receivers are known as ellipsoidal heights and are referenced to a simplified mathematical representation of the Earth known as the ellipsoid (for practical purposes an ellipsoid and a spheroid are the same). Ellipsoidal heights differ from geoid/AHD heights by between -30 and +70 metres across Australia. This is known as the geoid-ellipsoid separation, or N value. To convert ellipsoidal heights to geoid/AHD heights, a geoid model can be used. AUSGeoid09 is Australia's newest geoid model for converting ellipsoidal heights to AHD heights and is accurate to 0.03 metres across most of Australia. AUSGeoid09 supersedes early geoid models such as AUSGeoid98 and AUSGeoid93.
Mather (1971) reported that the first attempt at an astro-geodetic solution for the geoid in Australia was by Bomford for the Woomera region. As described in Bomford (1963) the real impetus for a new datum came from the requirements of the Woomera rocket range. Their requirement was to be able to accurately track rockets in flight. In 1962 and 1963 a geoid survey of the Woomera area confirmed that the existing geodetic datum being the Clarke 1858 spheroid Sydney origin did not fit the geoid. The spheroidal surface was found to be tilted by about 8" in an east-west direction relative to the geoid. The Woomera survey then permitted computations on the Clarke 1858 spheroid Sydney origin, to be adjusted to the required accuracy. However, it was Bomford's conclusion that it will therefore be wise to discontinue the use of the Clarke 1858 spheroid Sydney origin, as soon as the adjustment of the Geodetic Survey of Australia is completed in 1965.

Members of the National Mapping Astro Section mid-1960s; Dr Peter Bardulis (seated, Head of Section), Klaus Leppert (left) and Tony Bomford (right), unfortunately the names of the ladies are unknown.
An astro-geodetic geoid for Australia was produced by the United States Army Map Service in late 1966 and referred to the Australian Geodetic Datum (Fischer & Slutsky, 1967). This 1966 geoid was based on astro-geodetic observations recorded at approximately 600 Laplace stations and is known as the 1967 astro-geodetic solution. A further solution was made by Nat Map 1971. The 1971 solution used the astro-geodetic observations from approximately 1150 Laplace stations (Fryer, 1971).
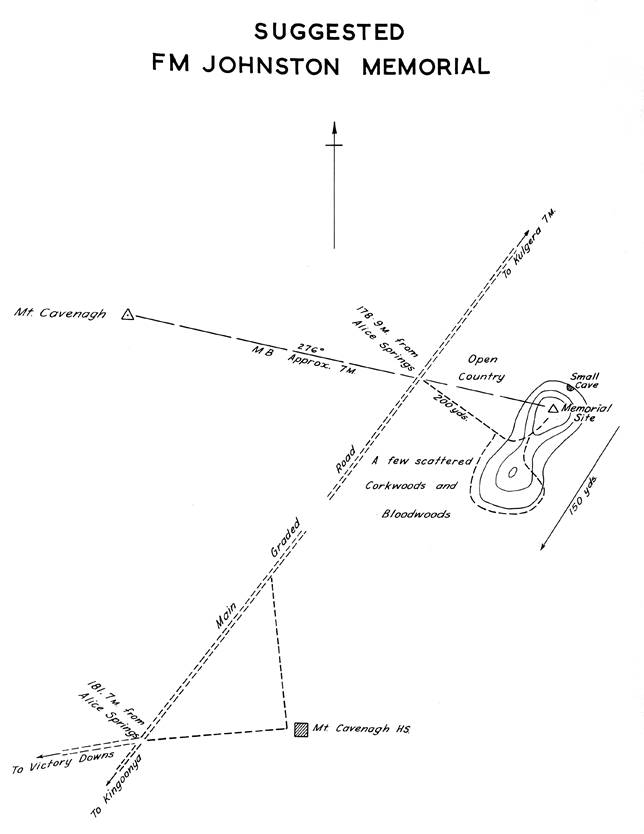
It would seem that the site for this originally named FM Johnston Memorial Station was agreed to be in the central region of Australia, around where the then Adelaide-Alice Springs road, now Stuart Highway, crossed the South Australian-Northern Territory border. While the exact instruction Nat Map’s Supervising Surveyor, Geodetic Branch, HA (Bill) Johnson was given regarding the choice of site is unknown, he reported :
|
Report on Selection of Site for 6 October 1964
Reference is made to instruction to me to examine and advise on a suitable site for a memorial to FM Johnston, previous Commonwealth Surveyor General. At the time of the discussion I mentioned that I thought a good site would be on one of the arkosic (granite) sandstone residuals near Mt. Cavenagh HS on the Kingoonya-Alice Springs road, and about 180 miles south of Alice Springs. On my recent return from the field I examined this site, which seemed even better than I remembered. The site suggested is on an arresting small residual about 200 yards east of the road at 178.9 miles from Alice Springs. The residual is on open gently rising high ground and although only 50 feet approximately above the general level of the surrounding high ground, it commands in every direction except for several residuals half a mile or further to the south-east, which however are too far from the road and the going too sandy and not so readily seen, as this suggested site. The northern end of the residual has abrupt, rough, top walls, which give an impressive effect, and there is a small cave at the base of the northern end. If it were so desired it would be possible to make a drive-on to the central saddle from the south-east side of the hill, which is about 150 yards long over all. From the foot of the western side of the saddle it is an easy, less than two minute climb to the top. The great drought that has scoured the Centre for over eight years has killed most of the mulga for hundreds of miles around and on this hill, leaving only hakea (corkwoods) and bloodwood eucalypts alive in the general vicinity. The dead mulga on the hill would best be removed by winching out, or cutting very low to the ground, if winching spoils the effect. There is plenty of good building stone. It is suggested the memorial be in the form of a well built 10 foot diameter by 9 foot high pudding shaped cairn, with 14 foot steel pole and 3' 6" overall vanes of heavy galvanized plate, with brass plaque set in the cairn and substantially hooked deep in the cairn. The vanes, which will be an irresistible test of every Australian and International marksman who passes, should be replaceable, though not without some difficulty and correct, socket spanners. The Ground Mark and Reference Marks should be laid out and connected to Mount Cavenagh before the cairn is built. The RM's should be clearly marked as such, welded and rivetted to 2½ or 3 inch rods set 30 inches in heavily reinforced massive concrete blocks. The whole memorial should be a typical cairn mark, slightly oversize, such as we have been erecting for nearly 11 years and some of which in South Australia have been standing without a rock displaced for over 100 years. Access sketch and location cutting from Kulgera 1: 250,000 scale map sheet attached.
|
On 13 October 1964, Nat Map’s Director BP Lambert wrote to the Surveyor General, Lands and Survey Branch, Northern Territory Administration, enclosing a copy HA Johnson’s report and sought his approval for the erection of such a memorial in his jurisdiction. Then interim Northern Territory Surveyor General, HM Hocking replied positively to Lambert on 3 November 1964. Lambert then informed all other members of the NMC on 6 November 1964 that approval for the memorial had been obtained and it was hoped to have it constructed during Nat Map’s 1965 field season.
|
COMMONWEALTH OF AUSTRALIA. TEL ADDRESS: "ASS TA DARWIN
IN REPLY PLEASE QUOTE: NO : : 64/3756 Lands and Survey Branch, NORTHERN TERRITORY ADMINISTRATION. DARWIN.
13th November, 1964
The Director of National Mapping, Division of National Mapping, Derwent House, University Avenue, CANBERRA CITY. A.C.T. F. M. JOHNSTON MEMORIAL GEODETIC STATION
I refer to your NM64/167 relative to the above matter. A staff surveyor from this Branch has made an inspection of this site and has forwarded the following comments on your selection : The site appears to be quite reasonable and should not affect any future road works in the vicinity. However, while there may be other considerations for the present selection which are not known to me, I feel that a better site would be a more prominent feature two miles further south and about 200 yards west of the road. My reasons for this are : Prominence The feature is a bare solid elongated dome of granite about 50-75 feet high, which can be seen for at least a mile in either direction from the north-south road as well as by traffic on the Victory Downs road. Position The feature is within sight of Mt. Cavenagh homestead which in itself would be a deterrent. Access This feature is about the same distance from the road as the suggested site, being about 200 yards over firm sand. There is no possibility of forming a drive-on to the top of the hill but I do not feel that this is a disadvantage as it is an easy five minutes climb to the top. I feel that monuments of this nature should have a small degree of difficulty of access as it can be assumed that the majority of those who take a closer look have a genuine interest and are not just looking for a place to scratch their name. Aspect This feature is bolder and more prominent than the suggested site and is not covered with scrub. Neither is there any likelihood of serious erosion or regrowth as there may be with the suggested site if the covering mulga trees are winched out. Connection Mt. Cavenagh Geodetic Station is clearly visible. The main feature against this second site would be the fact that all stone for the proposed cairn would have to be transported to the site, whereas it is available at the suggested site. Also all ground marks and reference marks would have to be grouted into the rock rather than set in massive concrete blocks. Sgd.) E.B.M. JAMES Staff Surveyor.
It is considered that Mr. Surveyor James' suggestions are worthy of consideration and, in this light, a copy of his report is forwarded with that end in view. Your further advice will be awaited. Yours faithfully, M.C. Hall, Surveyor General, N.T.
|
|
|
|
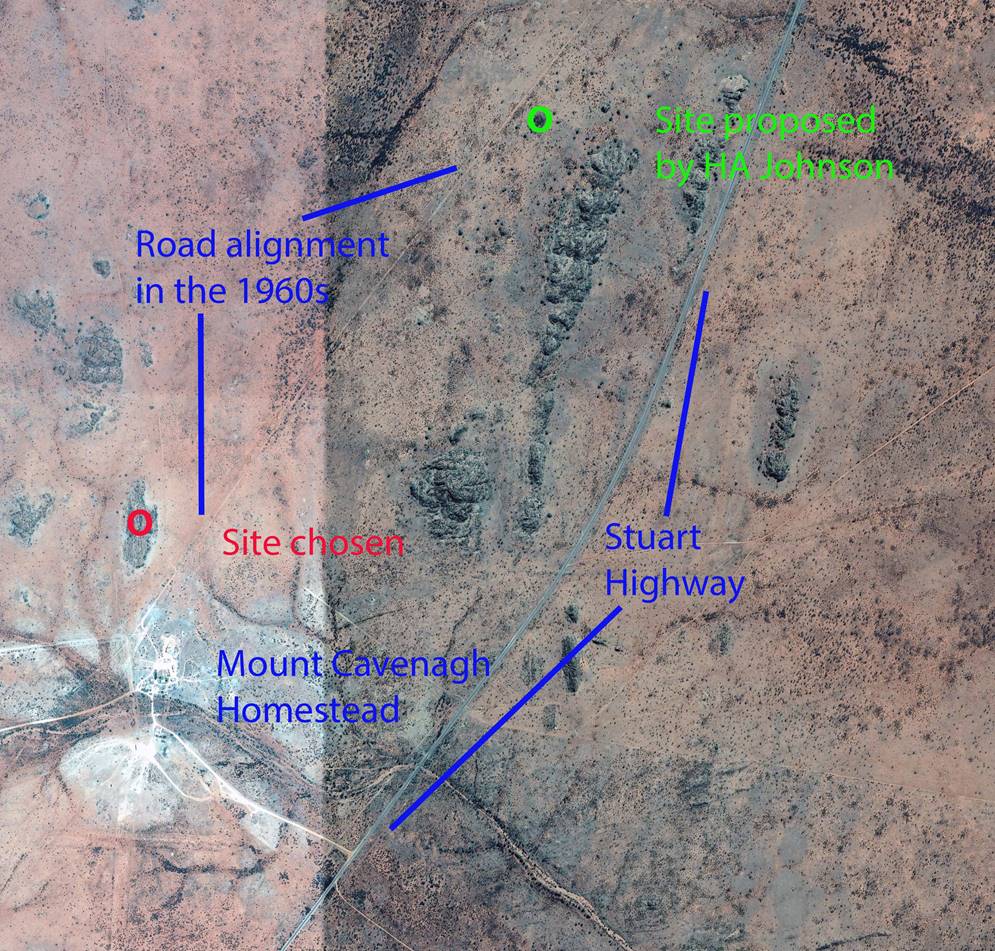
2018 Google Earth image showing the proposed and final site of the Johnston Geodetic Station in relation to Mount Cavenagh Homestead and the 1960s road and Stuart Highway alignments. |
Lambert replied to Hall on 19 November 1964, saying that James’ report would be provided to HA Johnson for him to make the final decision in 1965. During August 1965 there was a further exchange of correspondence between Nat Map and the NT Surveyor General about now incorporating the FM Johnston Memorial into a monument on the South Australia-Northern Territory border. This monument would be of similar construction to other such NT monuments and to maintain the same appearance the assistance of the NT Lands and Survey officer responsible for these other works was requested. Although now getting late in the Nat Map 1965 field season, Lambert was still keen to get the monument erected and indicated this in writing. With time running out in the 1965 field season, it appears that HA Johnston made the decision as to the site such that in October-November 1965, Nat Map with the assistance of two NT Lands and Survey officers erected the cairn where it stands today. Please see above Google Earth image showing the proposed and final site of the Johnston Geodetic Station in relation to Mount Cavenagh Homestead and the 1960s road and Stuart Highway alignments.
The Johnston Geodetic Station was planned to consist of a fourteen foot galvanized steel pole with four vanes, each of 4 feet x 2 feet x 3/32 inch galvanized plate, the same as used by Nat Map for the massive beacons in the New Guinea highlands, within a 9 foot diameter base, 10 foot high large stone pudding shaped cairn. During construction however, it was decided that the cairn would have a conical shape instead of the usual Nat Map pudding shape, and for appearances the granite and concrete was faced with a red sandstone veneer of thin flat stone. This stone had to be transported by vehicle from some distance away. Some of those constructing the cairn had had previous experience with erecting Nat Map cairns so there was some disquiet at the time at this now non-standard approach.
Twenty-one bags of cement, together with sufficient sand to make a three-to-one mixture, plus the necessary water was carried up the hill in containers strapped to Yukon packs. In addition, the rock for the veneer surface and much of the rock for filling the centre of the cairn also had to be carried up the hill. (The material statistics all man handled were given as 1¼ tons of cement and lime, 5 tons of sand, 1½ tons of facing rock and 300 gallons of water). The high prevailing temperature saw all members of the building team suffer the effects of heat exhaustion. All team members were grateful to the people at the nearby Mount Cavanagh homestead, for not only showing great interest in the work, but for also making shower facilities available.
|
1965 Nat Map Field Survey Party Members |
|
|
First order survey connection at the Johnston Geodetic Station : |
|
|
O J (Bob) Bobroff |
Surveyor Class 2 |
|
Bob Goldsworthy |
Technical Assistant Grade 2 |
|
|
|
|
First order survey connection at Cavenagh and Cecil : |
|
|
John Harris |
Surveyor Class 1 |
|
David Yates |
Field Assistant |
|
|
|
|
Monumentation : |
|
|
Ed Burke |
Technical Assistant Grade 2 |
|
John Ely |
Field Assistant (occupied Cavenagh with Ed Burke) |
|
Bill Sutherland |
Field Assistant |
|
Eddy Ainscow |
Field Assistant |
|
H A (Bill) Johnson |
Supervising Surveyor, Geodetic Survey Branch |
|
|
|
|
AM Sahariv |
Lands and Survey Branch, Northern Territory Administration |
|
Noel Hampton |
|

John Ely watching Bill Sutherland and Eddy Ainscow installing the vanes. The tent at right of picture is to protect the theodolite from sun and wind during first order angle observations to Cavenagh and Cecil
(courtesy Ed Burke 1965).
It was fitting that HA (Bill) Johnson (1907-1990) was a member of the monumentation team as this was the last cairn that Nat Map constructed. Almost 12 years earlier Johnson had been a member of the field party that built Nat Map’s first cairn at Moorkaie outside Broken Hill, New South Wales. During construction of the Johnston Geodetic Station Cinematographer John Carter of the Commonwealth Film Unit (please refer to photographs below) filmed the field survey part of the documentary Mapping Australia.
|
|
|
Cinematographer John Carter (left) with MRA-2 Tellurometer in centre background and filming camera right and Johnston Geodetic Station in 1966 (right) with its plinth and prior to installation of the bronze plaque (courtesy Denyse Goldsworthy 1965 and Peter Langhorne 1966).
With the completion of the cairn, on 10 November 1965 Lambert wrote to FM Johnston’s widow Eileen Johnston advising her of the memorial and its location. Eileen Johnston replied on 19 November, expressing her gratitude.
Next, Lambert informed the NT Surveyor General of the cairn’s completion on 17 November 1965. In that letter Lambert asked his appreciation be expressed to HM Hocking, Supervising Surveyor at Alice Springs for his ready cooperation in the project and for his making available Messrs AM Sahariv and Noel Hampton who so ably helped with the masonry to give it a professional appearance. Lambert then informed all other members of the NMC on 24 November 1964 of the cairn’s completion and supplied a copy of Eileen Johnston’s letter of thanks.
In May 1966, a Nat Map field party comprising RA Ford (1914-1994), Senior Technical Officer Grade 1 and PH Langhorne, Surveyor Class 1 and others while enroute from Melbourne to their survey area at Helen Springs, constructed the concrete plinth surrounding the cairn.
With the Australian Geodetic Datum (AGD66) adopted by the National Mapping Council and proclaimed in the Commonwealth Gazette in October 1966, the wording on the plaque to be installed in the Johnston station cairn was proposed. As indicated above it was to be the FM JOHNSTON MEMORIAL STATION. Following discussions with the Parliamentary Draftsman wording the proposed Offshore Petroleum Legislation, on 12 April 1967 Lambert advised the final wording was JOHNSTON GEODETIC STATION with the word origin replaced by the word datum in the accompanying text.
On 12 July 1967 HA Johnson reported that the plaque had been sent by air to Alice Springs where it will be collected by Mr Madden. All components (bolts, washers, plastibond, litharge [lead monoxide in red or reddish yellow solid employed as a drier in varnishes], caps to screw on 3 inch pipe inside the cairn) except glycerine and cement which can be bought in Alice Springs have been included and it is thought the plaque will be securely fixed on completion with small chance of removal. The plaque cost $116 from Mechanised Methods of Bourke Street, Melbourne; Mechanised Methods was a subsidiary company of the Arrow Engraving and Foundry Company of Tooronga Road, Glen Iris; this firm later cast the direction plaque for the Uluru station monument.
Senior Surveyor John Madden with assistant Alan Mould were temporarily released from the Nat Map Ground Marking for Aerodist field party and duly collected the plaque and installed it in the cairn in late July 1967. The photographs below were taken at that time.
Lambert subsequently informed all members of the NMC on 20 October 1967 that the plaque had been installed and provided them with copies of the photographs shown below.
With all aspects of the NMC’s resolution now fulfilled, Lambert authored a short article titled The Johnson Geodetic Survey Station. The article was published in The Australian Surveyor of June 1968, Vol.22, No.2, pp.93-95.
|
|
|
The Johnston Geodetic Station in July 1967 (XNATMAP photos).
Closing remarks
On 1 January 2000, Australia adopted an Earth centred or geocentric datum, namely the Geocentric Datum of Australia 1994 (GDA94). The GDA is a part of a global coordinate reference framework and is directly compatible with the Global Navigation Satellite Systems (GNSS). The change to GDA recognised how much our world now relies on global satellite positioning. Despite the Australian Geodetic Datum now being obsolete, the Johnston Geodetic Station / Johnston Origin retains its physical representation in the landscape, a reminder of the first time that Australia had a calculated origin or centre and a nationwide homogeneous network of horizontal positions.

The Johnston Geodetic Station in 2014 (courtesy August Jenny).

The Mt Cavenagh (identifier MTCV) AuScope site on the plain below the Johnston Geodetic Station in 2012. Far left is the GNSS antenna atop its monument and to the right from front to back are the data uplink transmitter, cabinets for the receiver, meteorological sensors and ancillary electronics and the solar panel assembly (courtesy Laurie McLean).
It is therefore somewhat unexpected today to find that the Johnston Geodetic Station now overlooks part of the technology that replaced it. To the west of the granite outcrop on which the Johnston Geodetic Station was constructed, is an AuScope site, please refer to photograph above. This is one of over one hundred such sites. Each site includes a GNSS receiver, antenna and meteorological sensors. Sites were selected such that the antenna monuments could be anchored to bedrock and support the most precise positioning applications. Remote sites are solar powered and are capable of streaming data in real-time. The meteorological sensors are to aid atmospheric studies.
The AuScope GNSS receivers are able to track existing and planned GPS constellations. The data gathered by the receiver’s aid in any refinement of the National Geospatial Reference System for monitoring crustal movement and continental deformation. The future is to ultimately remove the need for national systems having instead a single, global, homogenous and stable reference system.
References
AuScope (2014), accessed December 2014 at : http://www.auscope.org.au/overview/
Bomford, Anthony G (1963), The Woomera Geoid Surveys, 1962-63, Technical Report 3, Division of National Mapping.
Bomford, Anthony G (1964), Small Corrections to Astronomic Observations, The Australian Surveyor, Vol. 20, Issue 3, pp. 199-211.
Bomford, Anthony G (1967), The Geodetic Adjustment of Australia, 1963-1966, Survey Review, Vol. XIX, No. 144, pp. 52-71.
Bomford, Anthony G, Cook, David P and McCoy Frank J (1970), Astronomic Observations in the Division of National Mapping 1966-1970, Technical Report 10.
Bomford, Guy (1971), Geodesy, Oxford University Press, London, Ed. 3, 1971.
Fischer, Irene Kaminka (1960), An Astrogeodetic World Datum Based on the Flattening of 1/ 298.3, Journal of Geophysical Research, Vol.65, No.7, pp.2067-2076.
Fischer, Irene Kaminka (2005), Geodesy? What's That? My Personal Involvement in the Age-Old Quest for the Size and Shape of the Earth, iUniverse Inc., USA.
Fischer, Irene Kaminka & Slutsky, Mary (1967), A preliminary geoid chart of Australia, Australian Surveyor, Vol.21, No.8, pp.327-332.
Fischer, Irene Kaminka, Slutsky, Mary, Shirley, Francis Raymond and Wyatt, Phillip Y (1968), New pieces in the picture puzzle of an astrogeodetic geoid map of the world, Bulletin Geodesique, Vol.88, No.1, pp.199-221.
Ford, Reginald A (1979), The Division of National Mapping’s part in the Geodetic Survey of Australia, The Australian Surveyor, Vol. 29, No. 6, pp. 375-427; Vol. 29, No. 7, pp. 465-536; Vol. 29, No. 8, pp. 581-638.
Fricke, W., & Kopff, A. (1963), Fourth Fundamental Katalog (FK4), Astron. Rechen-Inst. Heidelberg.
Fryer, JG (1971), The Geoid in Australia - 1971, Technical Report 13, Division of National Mapping.
Kaula, William M (1961), A Geoid and World Geodetic System based on a Combination of Gravimetric, Astro-Geodetic and Satellite Data, National Aeronautics and Space Administration Technical Note D-702, NASA TND-702).
Leppert, Klaus (1973), Geodesy in Australia, 1956-72, Proceedings 16th Australian Survey Congress, Canberra, pp.A1-A6.
Lambert, Bruce P (1963), The Australian Geodetic Survey – An interim report on the utilisation of electronic distance measuring equipment, In Report of Proceedings, Conference of Commonwealth Survey Officers, Cambridge, 1963, Paper 8, pp. 72-75.
Lambert, Bruce P (1962), A Figure of the Earth for Australia, The Australian Surveyor, Vol.19, Issue 3, pp.178-185.
Lambert, Bruce P (1964), The Role of Laplace Observations in Geodetic Survey, The Australian Surveyor, Vol.20, Issue 2, pp.81-96.
Lines, John D (1992), Australia on Paper – The Story of Australian Mapping, Fortune Publications, Box Hill.
Mather, Ronald S (1972), The 1971 geoid for Australia and its significance in global geodesy, Journal of the Geological Society of Australia, Vol.19, No.1, pp.21-29.
National Aeronautics and Space Administration (NASA) (1971), NASA Directory of Observation Station Locations, Vol.1, 2nd Edition.
National Archives Australia (2018), NM71/195, Johnston F.M. Memorial - Johnston Geodetic Station, Barcode Number: 8241835, Series Number: A1575, Control Symbol: NM71/195.
National Mapping Council of Australia, (1972), The Australian Map Grid – Technical Manual, Special Publication 7.
National Mapping Council of Australia, (1986), The Australian Map Grid – Technical Manual, Special Publication 10.
Nash, David (2018), Personal communication providing access to his photographs of the Johnston Geodetic Station taken in September 1991 and available from the link on the External Sites page.
Laplace Correction
The Laplace correction, after Pierre-Simon Laplace (1749–1827), is used to relate a geodetic azimuth to an astronomical azimuth. Such a correction is made at a point called a Laplace Station, where the deflection of the vertical components is known. In a broader sense, the Laplace equations are used to connect the real physical world with a mathematical representation.
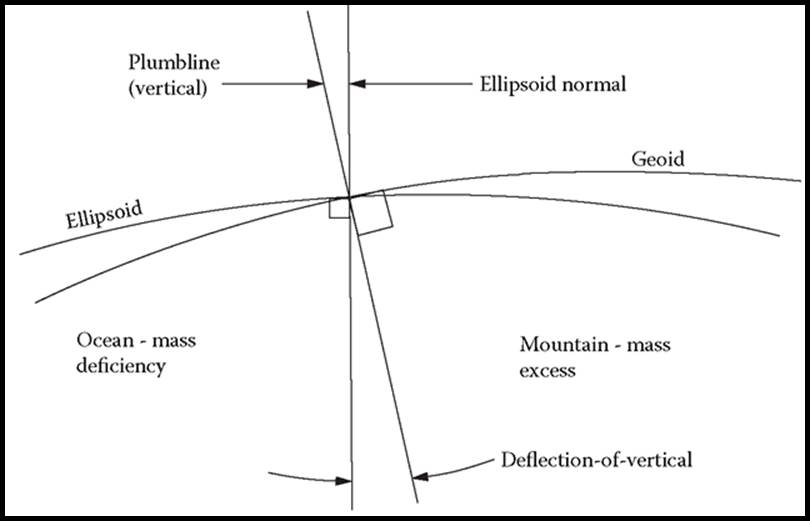
Figure A1 : Deflection of the Vertical
The mathematical ellipsoid/spheroid normal is perpendicular to the tangent to the curve of spheroid. In the physical world, the direction of the plumbline is the result of physical forces acting on an object. Refer Figure A1. Although the difference is not significant for many applications, at any given point in the terrain the direction of the spheroid normal and the direction of the plumbline differ and must be considered in geodetic computations. The direction of the normal at any point in the terrain is well defined and computable. Given the non-uniform distribution of mass within the Earth, however, the precise direction of the plumb line at the same point is less predictable. The difference between the spheroid normal and the vertical plumb line is called deflection of the vertical.
The spheroid surface is not necessarily parallel with the level surface of the terrain or geoid. The angular amount by which the two surfaces are not parallel is given by the deflection of the vertical and is expressed in terms of a north/south or in meridian component and an east/west or in prime vertical component.
Astronomical observations of directions to stars are gravity based and yield astronomical positions. Survey (azimuth and distance from a known point to an unknown point) derived positions are spheroidal based and provide geodetic positions. The two systems are related by the Laplace equations.
Deflection in meridian (ξ or east/west direction) :
ξ = Astronomic latitude - Geodetic latitude (1)
Deflection in prime vertical (η or north/south direction) :
η = (Astronomic longitude - Geodetic longitude) cos (Geodetic latitude) (2)
Azimuth
η = (Astronomic azimuth - Geodetic azimuth) cot (Geodetic latitude) (3)
Equations (2) and (3) show that deflection in prime vertical (η) can be deduced from the difference of either the astronomic and geodetic longitudes or of the astronomic and geodetic azimuths. As the two values for η must be the same then combining equations (2) and (3) gives :
Geodetic azimuth = Astronomic azimuth –
[(Astronomic longitude - Geodetic longitude) sin (Geodetic latitude)] (4)
Equation (4) is most important as it enables the geodetic azimuth at any Laplace station to be determined from a combination of astronomical azimuth and longitude observations. Laplace stations therefore permit an independent check to be made on a survey’s derived azimuth especially on long geodetic traverses such as occurred in Australia. In the 1966 Australian adjustment, of the 2,506 geodetic stations 533 were also Laplace stations.
In Australia, however, the Laplace observations were also used to establish the central origin for the Australian spheroid following the 1965 adoption of the parameters for the Australian National Spheroid (ANS). The central origin would ultimately have geodetic coordinates such that the resulting means of the deflections of the vertical (ξ and η from above) at a selected 275 Laplace stations were close to zero.
The starting position was the May 1965 adjustment which used the coordinates of trigonometrical station Grundy as the central origin. Grundy was chosen as its coordinates, as determined on the 165 spheroid, remained unchanged when they were recalculated on the ANS. This coincidence was a strong indication that the coordinates of Grundy were close to those of the central origin; within 1¼° as it turned out.
With the geodetic coordinates of the 275 Laplace stations now all originating from Grundy, simplistically an azimuth and distance could be calculated to each Laplace station from Grundy, the starting central origin. At each Laplace station the deflections of the vertical could also be determined as explained above. By inspection of the deflections a new set of coordinates for the central origin could now be determined.
Using these new coordinates for the central origin and the previously computed and now fixed azimuths and distances to the Laplace stations, new geodetic coordinates for each of the Laplace stations could be determined. As the astronomic coordinates for the Laplace stations would remain static, new deflections of the vertical at each Laplace station could then be determined. By iteration, an optimum set of coordinates for the central origin could be found such that the consequential geodetic coordinates for the Laplace stations resulted in the means of the deflections of the vertical being close to zero.
In 1965, the accepted coordinates for the central origin, based on the 275 Laplace stations, resulted in a mean deflection of +0.15" in meridian and -0.36" in prime vertical. Later testing revealed that this result could not be improved even if a much larger number of Laplace stations were used. The central origin so determined became known as the Johnston Origin and was monumented as the Johnston Geodetic Station.